
Uma abordagem
para
C A L C U L U S
Tabela de conteúdos | Home
Os pontos de viragem de um gráfico

DISSE QUE UMA FUNÇÃO f(x) tem um valor máximo relativo a x = a,
se f(a) for maior do que qualquer valor imediatamente anterior ou seguinte.
Dizemos que uma função f(x) tem um valor mínimo relativo a x = b,
se f(b) é inferior a qualquer valor imediatamente anterior ou seguinte.
Aganhar, outros valores da função podem, de facto, ser inferiores. Com esse entendimento, então, vamos abandonar o termo relativo.
O valor da função, o valor de y, a um máximo ou a um mínimo é chamado de valor extremo.
Agora, o que caracteriza o gráfico a um valor extremo?

A tangente à curva é horizontal. Vemos isto nos pontos A e B. A inclinação de cada linha tangente — a derivada quando avaliada em a ou b — é 0.
f ‘(x) = 0.
mais, em pontos imediatamente à esquerda de um máximo — num ponto C — a inclinação da tangente é positiva: f ‘(x) > 0. Enquanto nos pontos imediatamente à direita — num ponto D — a inclinação é negativa: f ‘(x)
Por outras palavras, num máximo, f ‘(x) muda o sinal de + para – .
Num mínimo, f ‘(x) muda o sinal de – para + . Podemos ver que nos pontos E e F.
também podemos observar que no máximo, em A, o gráfico é côncavo para baixo. (Tópico 14 do Precalculus.) Enquanto que no mínimo, em B, é côncavo para cima.
Um valor de x no qual a função tem um valor máximo ou mínimo é chamado um valor crítico. Na figura —

— os valores críticos são x = a e x = b.
Os valores críticos determinam pontos de viragem, em que a tangente é paralela ao eixo x. Os valores críticos — se existirem — serão as soluções para f ‘(x) = 0.
Exemplo 1. Deixar f(x) = x2 – 6x + 5.
Existe algum valor crítico — algum ponto de viragem? Em caso afirmativo, determinam um máximo ou um mínimo? E quais são os coördinates no gráfico desse máximo ou mínimo?
Solução. f ‘(x) = 2x – 6 = 0 implica x = 3. (Lição 9 de Álgebra.)
x = 3 é o único valor crítico. É o x-coördinate do ponto de viragem. Para determinar o y-coördinate, avaliar f a esse valor crítico — avaliar f(3):
| f(x) | == | x2 – 6x + 5 |
| f(3) | = | 32 – 6- 3 + 5 |
O valor extremo é -4. Para ver se é um máximo ou um mínimo, neste caso podemos simplesmente olhar para o gráfico.
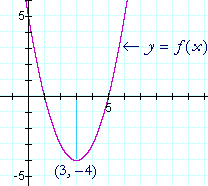
f(x) é uma parábola, e podemos ver que o ponto de viragem é um mínimo.
Ao encontrarmos o valor de x onde a derivada é 0, descobrimos então que o vértice da parábola está em (3, -4).
Mas nem sempre conseguiremos olhar para o gráfico. A condição algébrica para um mínimo é que f ‘(x) muda de sinal de – para + . Vemos isto nos pontos E, B, F acima. O valor da inclinação está a aumentar.
Agora dizer que a inclinação está a aumentar, quer dizer que, a um valor crítico, a segunda derivada (Lição 9) — que é a taxa de variação da inclinação — é positiva.
Again, aqui é f(x):
| f(x) | = | x2 – 6x + 5. |
| f ‘(x) | = | 2x – 6. |
| f ”(x) | >>>/td>>>>/td> |
f ” avaliado no valor crítico 3 — f”(3) = 2 — é positivo. Isto diz-nos algébricamente que o valor crítico 3 determina um valor mínimo.
Condições suficientes

Podemos agora afirmar estas condições suficientes para valores extremos de uma função num valor crítico a:
A função tem um valor mínimo a x = a se f ‘(a) = 0
e f ”(a) = um número positivo.
A função tem um valor máximo a x = a if f ‘(a) = 0
and f ”(a) = um número negativo.
No caso do máximo, a inclinação da tangente está a diminuir — está a passar de positivo para negativo. Podemos ver isso nos pontos C, A, D.
Exemplo 2. Let f(x) = 2×3- 9×2 + 12x – 3.
Exemplo 2. Primeiro, existem valores críticos — soluções para f ‘(x) = 0 — e determinam um máximo ou um mínimo? E quais são os coördinates no gráfico desse máximo ou mínimo? Onde estão os pontos de viragem?
| Solução. f ‘(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) |
implies:
x = 1 ou x = 2.
(Lição 37 de Álgebra.)
Estes são os valores críticos. Cada um deles determina um máximo ou determina um mínimo? Para responder, temos de avaliar a segunda derivada a cada valor.
| f ‘(x) | = | 6×2 – 18x + 12. |
| f ”(x) | = | 12x – 18. |
| f ”(1) | >= | 12 – 18 = -6. |
A segunda derivada é negativa. A função tem, portanto, um máximo em x = 1.
Para encontrar o y-coördinate — o valor extremo — a esse máximo avaliamos f(1):
| f(x) | == | 2×3- 9×2 + 12x – 3 |
| f(1) | >==/td> | 2 – 9 + 12 – 3 |
O máximo ocorre no ponto (1, 2).
P>Próximo, faz x = 2 determinar um máximo ou um mínimo?
| f ”(x) | = | 12x – 18. |
| f ”(2) | >=>/td> | 24 – 18 = 6. |
A segunda derivada é positiva. A função tem portanto um mínimo em x = 2.
Para encontrar o y-coördinate — o valor extremo — nesse mínimo, avaliamos f(2):
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | ==/td>>>16 – 36 + 24 – 3 | |
O mínimo ocorre no ponto (2, 1).
Aqui está de facto o gráfico de f(x):
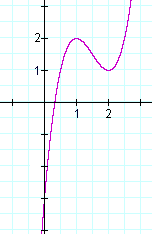
Soluções a f ”(x) = 0 indicam um ponto de inflexão nessas soluções, não um máximo ou mínimo. Um exemplo é y = x3. y” = 6x = 0 implica x = 0. Mas x = 0 é um ponto de inflexão no gráfico de y = x3, não um máximo ou mínimo.
Outro exemplo é y = pecado x. As soluções para y” = 0 são os múltiplos de π, que são pontos de inflexão.
Problema 1. Encontre os coördinates do vértice da parábola,
y = x2 – 8x + 1.
Para ver a resposta, passe o rato sobre a área colorida.
Para cobrir novamente a resposta, clique em “Refresh” (“Reload”).
Faça você mesmo o problema primeiro!
y’ = 2x – 8 = 0.
Isso implica x = 4. Isso é o x-coördinate do vértice. Para encontrar o y-coördinate, avaliar y em x = 4:
y = 42 – 8- 4 + 1 = -15.
O vértice está em (4, -15).
Problema 2. Examinar cada função para máximos e mínimos.
a) y = x3 – 3×2 + 2.
y’ = 3×2 – 6x = 3x(x – 2) = 0 implica
x = 0 ou x = 2.
y”(x) = 6x – 6.
y”(0) = -6.
A segunda derivada é negativa. Isso significa que há um máximo em x = 0. Esse valor máximo é
y”(0) = 2.
Next,
y”(2) = 12 – 6 = 6.
A segunda derivada é positiva. Isso significa que há um mínimo em x = 2. Esse valor mínimo é
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
At x = 1 há um máximo de y = 17.
Em x = -2 há um mínimo de y = -10.
c) y = 2×3 + 3×2 + 12 x – 4.
Desde f ‘(x) = 0 não tem soluções reais, não há valores extremos.