
Een benadering
tot
C A L C U L U S
Inhoudsopgave | Home
De omslagpunten van een grafiek

WE ZEGGEN DAT EEN FUNCTIE f(x) een relatieve maximumwaarde heeft bij x = a,
als f(a) groter is dan elke waarde die er onmiddellijk aan voorafgaat of erop volgt.
We noemen het een “relatief” maximum, omdat andere waarden van de functie in feite groter kunnen zijn.
We zeggen dat een functie f(x) een relatieve minimumwaarde heeft bij x = b,
als f(b) kleiner is dan elke waarde die onmiddellijk voorafgaat of volgt.
Ook hier geldt dat andere waarden van de functie in feite kleiner kunnen zijn. Met dat begrip laten we dus de term relatief vallen.
De waarde van de functie, de waarde van y, bij ofwel een maximum ofwel een minimum wordt een extreme waarde genoemd.
Wat kenmerkt nu de grafiek bij een extreme waarde?

De raaklijn aan de kromme is horizontaal. We zien dit bij de punten A en B. De helling van elke raaklijn — de afgeleide bij evaluatie in a of b — is 0.
f ‘(x) = 0.
Meer nog, in punten direct links van een maximum — in een punt C — is de helling van de raaklijn positief: f ‘(x) > 0. Terwijl in punten direct rechts daarvan — in een punt D — de richtingscoëfficiënt negatief is: f ‘(x)
Met andere woorden, bij een maximum verandert f ‘(x) van teken van + naar – .
Bij een minimum verandert f ‘(x) van teken van – naar + . We zien dat bij de punten E en F.
We zien ook dat bij een maximum, bij A, de grafiek concaaf naar beneden is. (Onderwerp 14 van Precalculus.) Terwijl bij een minimum, bij B, de grafiek concaaf naar boven is.
Een waarde van x waarbij de functie ofwel een maximum ofwel een minimum heeft, wordt een kritische waarde genoemd. In de figuur —

— zijn de kritische waarden x = a en x = b.
De kritische waarden bepalen omslagpunten, waarbij de raaklijn evenwijdig is aan de x-as. De kritische waarden — als die er zijn — zullen de oplossingen zijn van f ‘(x) = 0.
Voorbeeld 1. Zij f(x) = x2 – 6x + 5.
Zijn er kritische waarden — omslagpunten? Zo ja, bepalen die een maximum of een minimum? En wat zijn de coördinaten op de grafiek van dat maximum of minimum?
Oplossing. f ‘(x) = 2x – 6 = 0 impliceert x = 3. (Les 9 van Algebra.)
x = 3 is de enige kritische waarde. Het is de x-coördinaat van het omslagpunt. Om de y-coördinaat te bepalen, waardeer je f bij die kritische waarde — waardeer f(3):
| f(x) | = | x2 – 6x + 5 |
| f(3) | = | 32 – 6- 3 + 5 |
| -4. | ||
De extreme waarde is -4. Om te zien of het een maximum of een minimum is, kunnen we in dit geval gewoon naar de grafiek kijken.
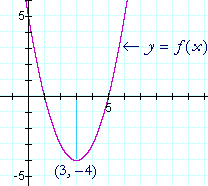
f(x) is een parabool, en we kunnen zien dat het omslagpunt een minimum is.
Door de waarde van x te vinden waarbij de afgeleide 0 is, hebben we dus ontdekt dat het hoekpunt van de parabool op (3, -4) ligt.
Maar we zullen niet altijd in staat zijn naar de grafiek te kijken. De algebraïsche voorwaarde voor een minimum is dat f ‘(x) van teken verandert van – naar + . We zien dit bij de punten E, B, F hierboven. De waarde van de helling neemt toe.
Nu zeggen dat de helling toeneemt, is zeggen dat, bij een kritische waarde, de tweede afgeleide (Les 9) — dat is de veranderingssnelheid van de helling — positief is.
Ook hier is f(x):
| f(x) | = | x2 – 6x + 5. |
| f ‘(x) | = | 2x – 6. |
| f ”(x) | = | |
f ” geëvalueerd op de kritische waarde 3 — f”(3) = 2 — is positief. Dit vertelt ons algebraïsch dat de kritische waarde 3 een minimum bepaalt.
Voldoende voorwaarden

We kunnen nu deze voldoende voorwaarden stellen voor extreme waarden van een functie bij een kritische waarde a:
De functie heeft een minimumwaarde bij x = a als f ‘(a) = 0
en f ”(a) = een positief getal.
De functie heeft een maximum waarde bij x = a als f ‘(a) = 0
en f ”(a) = een negatief getal.
In het geval van het maximum neemt de richtingscoëfficiënt van de raaklijn af — hij gaat van positief naar negatief. We zien dat bij de punten C, A, D.
Voorbeeld 2. Zij f(x) = 2×3- 9×2 + 12x – 3.
Zijn er extreme waarden? Ten eerste, zijn er kritische waarden — oplossingen voor f ‘(x) = 0 — en bepalen die een maximum of een minimum? En wat zijn de coördinaten op de grafiek van dat maximum of minimum? Waar liggen de omslagpunten?
| Oplossing. f ‘(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) |
| = | 6(x – 1)(x – 2) | |
| = | 0 | |
betekent:
x = 1 of x = 2.
(Les 37 van Algebra.)
Dat zijn de kritische waarden. Bepaalt elk een maximum of bepaalt het een minimum? Om hierop te antwoorden moeten we de tweede afgeleide bij elke waarde bepalen.
| f ‘(x) | = | 6×2 – 18x + 12. |
| f ”(x) | = | 12x – 18. |
| f ”(1) | = | 12 – 18 = -6. |
De tweede afgeleide is negatief. De functie heeft dus een maximum bij x = 1.
Om de y-coördinaat — de extreme waarde — bij dat maximum te vinden, evalueren we f(1):
| f(x) | = | 2×3- 9×2 + 12x – 3 |
| f(1) | = | 2 – 9 + 12 – 3 |
| = | ||
Het maximum treedt op in het punt (1, 2).
Volgende, bepaalt x = 2 een maximum of een minimum?
| f ”(x) | = | 12x – 18. |
| f ”(2) | = | 24 – 18 = 6. |
De tweede afgeleide is positief. De functie heeft dus een minimum bij x = 2.
Om de y-coördinaat — de extreme waarde — bij dat minimum te vinden, berekenen we f(2):
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | = | 16 – 36 + 24 – 3 |
| = | ||
Het minimum treedt op in het punt (2, 1).
Hier is in feite de grafiek van f(x):
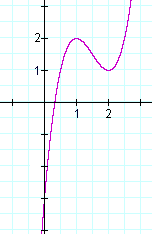
Oplossingen voor f ”(x) = 0 geven bij die oplossingen een buigpunt aan, niet een maximum of minimum. Een voorbeeld is y = x3. y” = 6x = 0 impliceert x = 0. Maar x = 0 is een buigpunt in de grafiek van y = x3, geen maximum of minimum.
Een ander voorbeeld is y = sin x. De oplossingen voor y” = 0 zijn de veelvouden van π, die buigpunten zijn.
Opgave 1. Vind de coördinaten van het hoekpunt van de parabool,
y = x2 – 8x + 1.
Om het antwoord te zien, ga met je muis over het gekleurde gebied.
Om het antwoord weer te zien, klik op “Vernieuwen” (“Reload”).
Doe het probleem eerst zelf!
y’ = 2x – 8 = 0.
Dat impliceert x = 4. Dat is de x-coördinaat van het hoekpunt. Om de y-coördinaat te vinden, waardeer je y bij x = 4:
y = 42 – 8- 4 + 1 = -15.
Het hoekpunt ligt op (4, -15).
Opgave 2. Onderzoek elke functie op maxima en minima.
a) y = x3 – 3×2 + 2.
y’ = 3×2 – 6x = 3x(x – 2) = 0 impliceert
x = 0 of x = 2.
y”(x) = 6x – 6.
y”(0) = -6.
De tweede afgeleide is negatief. Dat betekent dat er een maximum is bij x = 0. Die maximumwaarde is
y(0) = 2.
Volgende,
y”(2) = 12 – 6 = 6.
De tweede afgeleide is positief. Dat betekent dat er een minimum is bij x = 2. Die minimumwaarde is
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
Bij x = 1 is er een maximum van y = 17.
Bij x = -2 is er een minimum van y = -10.
c) y = 2×3 + 3×2 + 12 x – 4.
Omdat f ‘(x) = 0 geen reële oplossingen heeft, zijn er geen extreme waarden.