
Podejście
do
C A L C U L U S
Spis treści | Strona główna
Punkty zwrotne wykresu

MÓWIMY, ŻE FUNKCJA f(x) ma względną wartość maksymalną w punkcie x = a,
jeśli f(a) jest większa niż jakakolwiek wartość bezpośrednio ją poprzedzająca lub następująca po niej.
Nazywamy to „względnym” maksimum, ponieważ inne wartości funkcji mogą być w rzeczywistości większe.
Mówimy, że funkcja f(x) ma względne minimum przy x = b,
jeśli f(b) jest mniejsza niż jakakolwiek wartość bezpośrednio poprzedzająca lub następująca.
Ponownie, inne wartości funkcji mogą być w rzeczywistości mniejsze. Z takim rozumieniem porzucimy więc termin względny.
Wartość funkcji, wartość y, przy maksimum lub minimum nazywamy wartością ekstremalną.
Co charakteryzuje wykres przy wartości ekstremalnej?

Styczna do krzywej jest pozioma. Widzimy to w punktach A i B. Nachylenie każdej stycznej — pochodnej obliczonej w punkcie a lub b — wynosi 0.
f '(x) = 0.
Co więcej, w punktach położonych bezpośrednio na lewo od maksimum — w punkcie C — nachylenie stycznej jest dodatnie: f '(x) > 0. Natomiast w punktach położonych bezpośrednio po prawej stronie — w punkcie D — nachylenie jest ujemne: f '(x)
Innymi słowy, w punkcie maksymalnym f '(x) zmienia znak z + na – .
W punkcie minimalnym f '(x) zmienia znak z – na + . Widzimy to w punktach E i F.
Możemy również zauważyć, że w punkcie maksymalnym, w punkcie A, wykres jest wklęsły w dół. (Temat 14 z Precalculus.) Natomiast w minimum, w punkcie B, wykres jest wklęsły do góry.
Wartość x, przy której funkcja ma maksimum lub minimum, nazywamy wartością krytyczną. Na rysunku —

— wartościami krytycznymi są x = a i x = b.
Wartości krytyczne określają punkty zwrotne, w których styczna jest równoległa do osi x. Wartości krytyczne — jeśli istnieją — będą rozwiązaniami f '(x) = 0.
Przykład 1. Niech f(x) = x2 – 6x + 5.
Czy istnieją jakieś wartości krytyczne — jakieś punkty zwrotne? Jeśli tak, to czy wyznaczają one maksimum czy minimum? I jakie są współrzędne na wykresie tego maksimum lub minimum?
Rozwiązanie. f '(x) = 2x – 6 = 0 implikuje x = 3. (Lekcja 9 Algebry.)
x = 3 jest jedyną wartością krytyczną. Jest to współrzędna x punktu zwrotnego. Aby wyznaczyć współrzędną y, oceń f przy tej wartości krytycznej – oceń f(3):
| f(x) | = | x2 – 6x + 5 |
| f(3) | = | 32 – 6- 3 + 5 |
| = | -4. | |
Wartość skrajna wynosi -4. Aby sprawdzić, czy jest to maksimum czy minimum, w tym przypadku możemy po prostu spojrzeć na wykres.
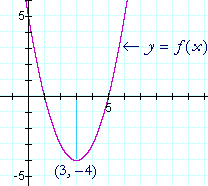
f(x) jest parabolą i widzimy, że punktem zwrotnym jest minimum.
Znajdując wartość x, dla której pochodna wynosi 0, odkryliśmy, że wierzchołek paraboli znajduje się w punkcie (3, -4).
Nie zawsze jednak będziemy mogli spojrzeć na wykres. Algebraicznym warunkiem minimum jest to, że f '(x) zmienia znak z – na + . Widzimy to w punktach E, B, F powyżej. Wartość nachylenia jest rosnąca.
Teraz powiedzieć, że nachylenie jest rosnące, to powiedzieć, że przy wartości krytycznej druga pochodna (Lekcja 9) — czyli szybkość zmiany nachylenia — jest dodatnia.
Ponownie, oto f(x):
| f(x) | = | x2 – 6x + 5. |
| f '(x) | = | 2x – 6. |
| f ”(x) | = | |
f ” oceniana przy wartości krytycznej 3 — f”(3) = 2 — jest dodatnia. To mówi nam algebraicznie, że wartość krytyczna 3 wyznacza minimum.
Warunki dostateczne

Możemy teraz podać te warunki dostateczne dla wartości ekstremalnych funkcji przy wartości krytycznej a:
Funkcja ma wartość minimalną przy x = a, jeśli f '(a) = 0
i f ”(a) = liczba dodatnia.
Funkcja ma wartość maksymalną w punkcie x = a, jeżeli f '(a) = 0
i f ”(a) = liczba ujemna.
W przypadku maksimum, nachylenie stycznej maleje — przechodzi z wartości dodatniej do ujemnej. Widzimy to w punktach C, A, D.
Przykład 2. Niech f(x) = 2×3- 9×2 + 12x – 3.
Czy istnieją jakieś wartości ekstremalne? Po pierwsze, czy istnieją wartości krytyczne – rozwiązania f '(x) = 0 – i czy wyznaczają one maksimum lub minimum? I jakie są współrzędne na wykresie tego maksimum lub minimum? Gdzie są punkty zwrotne?
| Rozwiązanie. f '(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) |
| = | 6(x – 1)(x – 2) | |
| = | 0 | |
przypuszcza:
x = 1 lub x = 2.
(Lekcja 37 Algebry.)
To są wartości krytyczne. Czy każda z nich wyznacza maksimum czy minimum? Aby odpowiedzieć, musimy ocenić drugą pochodną przy każdej wartości.
| f '(x) | = | 6×2 – 18x + 12. |
| f ”(x) | = | 12x – 18. |
| f ”(1) | = | 12 – 18 = -6. |
Druga pochodna jest ujemna. Funkcja ma zatem maksimum w punkcie x = 1.
Aby znaleźć współrzędną y – wartość ekstremalną – w tym maksimum, obliczamy f(1):
| f(x) | = | 2×3- 9×2 + 12x – 3 |
| f(1) | = | . 2 – 9 + 12 – 3 |
| = | ||
Maksimum występuje w punkcie (1, 2).
Następnie, czy x = 2 wyznacza maksimum czy minimum?
| f ”(x) | = | 12x – 18. |
| f ”(2) | = | 24 – 18 = 6. |
Druga pochodna jest dodatnia. Funkcja ma zatem minimum przy x = 2.
Aby znaleźć współrzędną y — wartość ekstremalną — przy tym minimum, oceniamy f(2):
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | = | 16 – 36 + 24 – 3 |
| . | ||
| = | ||
Minimum występuje w punkcie (2, 1).
Tutaj w rzeczywistości znajduje się wykres f(x):
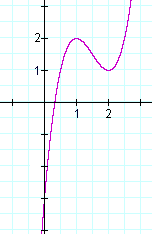
Rozwiązania f ”(x) = 0 wskazują na punkt przegięcia w tych rozwiązaniach, a nie na maksimum lub minimum. Przykładem jest y = x3. y” = 6x = 0 implikuje x = 0. Ale x = 0 jest punktem przegięcia na wykresie y = x3, a nie maksimum lub minimum.
Innym przykładem jest y = sin x. Rozwiązania y” = 0 są wielokrotnościami π, które są punktami przegięcia.
Problem 1. Znajdź współliniowe wierzchołka paraboli,
y = x2 – 8x + 1.
Aby zobaczyć odpowiedź, najedź myszką na kolorowy obszar.
Aby ponownie wyświetlić odpowiedź, kliknij przycisk „Odśwież” („Reload”).
Zrób to najpierw sam!
y' = 2x – 8 = 0.
To implikuje, że x = 4. To jest współrzędna x wierzchołka. Aby znaleźć współrzędną y, oblicz y przy x = 4:
y = 42 – 8- 4 + 1 = -15.
Więzeł znajduje się w punkcie (4, -15).
Zadanie 2. Zbadaj każdą z funkcji pod kątem maksimów i minimów.
a) y = x3 – 3×2 + 2.
y' = 3×2 – 6x = 3x(x – 2) = 0 implikuje
x = 0 lub x = 2.
y”(x) = 6x – 6.
y”(0) = -6.
Druga pochodna jest ujemna. Oznacza to, że istnieje maksimum w punkcie x = 0. Ta maksymalna wartość to
y(0) = 2.
Następnie,
y”(2) = 12 – 6 = 6.
Druga pochodna jest dodatnia. Oznacza to, że istnieje minimum w punkcie x = 2. To minimum wynosi
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
W punkcie x = 1 występuje maksimum y = 17.
Przy x = -2 występuje minimum y = -10.
c) y = 2×3 + 3×2 + 12 x – 4.
Ponieważ f '(x) = 0 nie ma rozwiązań rzeczywistych, nie istnieją wartości ekstremalne.
C) y = 2×3 + 3×2 + 12 x – 4.
Ponieważ f '(x) = 0 nie ma rozwiązań rzeczywistych, nie ma wartości ekstremalnych.