
Eine Annäherung
an
C A L C U L U S
Inhaltsverzeichnis | Home
Die Wendepunkte eines Graphen

Wir sagen, dass eine FUNKTION f(x) einen relativen Maximalwert bei x = a hat,
wenn f(a) größer ist als jeder unmittelbar vorangehende oder nachfolgende Wert.
Wir nennen es ein „relatives“ Maximum, weil andere Werte der Funktion tatsächlich größer sein können.
Wir sagen, dass eine Funktion f(x) einen relativen Minimalwert bei x = b hat,
wenn f(b) kleiner ist als jeder Wert, der unmittelbar vorausgeht oder folgt.
Auch hier gilt, dass andere Werte der Funktion tatsächlich kleiner sein können. Mit diesem Verständnis lassen wir also den Begriff relativ weg.
Der Wert der Funktion, der Wert von y, bei einem Maximum oder einem Minimum wird Extremwert genannt.
Was charakterisiert nun den Graphen bei einem Extremwert?

Die Tangente an die Kurve ist horizontal. Das sehen wir an den Punkten A und B. Die Steigung jeder Tangente — die Ableitung, wenn sie bei a oder b ausgewertet wird — ist 0.
f ‚(x) = 0.
Darüber hinaus ist an Punkten unmittelbar links von einem Maximum — am Punkt C — die Steigung der Tangente positiv: f ‚(x) > 0. Während an den Punkten unmittelbar rechts davon — im Punkt D — die Steigung negativ ist: f ‚(x)
Mit anderen Worten: Bei einem Maximum wechselt f ‚(x) das Vorzeichen von + zu -.
Bei einem Minimum wechselt f ‚(x) das Vorzeichen von – zu + . Das sehen wir an den Punkten E und F.
Wir können auch beobachten, dass bei einem Maximum, bei A, der Graph nach unten konkav ist. (Thema 14 von Precalculus.) Während er bei einem Minimum, bei B, konkav nach oben ist.
Ein Wert von x, bei dem die Funktion entweder ein Maximum oder ein Minimum hat, wird als kritischer Wert bezeichnet. In der Abbildung —

— sind die kritischen Werte x = a und x = b.
Die kritischen Werte bestimmen Wendepunkte, bei denen die Tangente parallel zur x-Achse verläuft. Die kritischen Werte – falls vorhanden – sind die Lösungen von f ‚(x) = 0.
Beispiel 1. Es sei f(x) = x2 – 6x + 5.
Gibt es irgendwelche kritischen Werte – irgendwelche Wendepunkte? Wenn ja, bestimmen sie ein Maximum oder ein Minimum? Und was sind die Koördinaten auf dem Graphen dieses Maximums oder Minimums?
Lösung: f ‚(x) = 2x – 6 = 0 impliziert x = 3. (Lektion 9 der Algebra.)
x = 3 ist der einzige kritische Wert. Er ist die x-Koordinate des Wendepunkts. Um die y-Kördinate zu bestimmen, werte f an diesem kritischen Wert aus – werte f(3) aus:
| f(x) | = | x2 – 6x + 5 |
| f(3) | = | 32 – 6- 3 + 5 |
| = | -4. | |
Der Extremwert ist -4. Um zu sehen, ob es sich in diesem Fall um ein Maximum oder ein Minimum handelt, können wir einfach den Graphen betrachten.
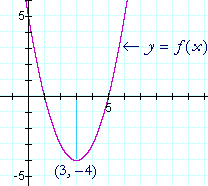
f(x) ist eine Parabel, und wir können sehen, dass der Wendepunkt ein Minimum ist.
Indem wir den Wert von x finden, bei dem die Ableitung 0 ist, haben wir also entdeckt, dass der Scheitelpunkt der Parabel bei (3, -4) liegt.
Aber wir werden nicht immer in der Lage sein, den Graphen zu betrachten. Die algebraische Bedingung für ein Minimum ist, dass f ‚(x) das Vorzeichen von – nach + wechselt. Dies sehen wir an den Punkten E, B, F oben. Der Wert der Steigung ist steigend.
Nun zu sagen, dass die Steigung steigend ist, bedeutet, dass bei einem kritischen Wert die zweite Ableitung (Lektion 9) – die Änderungsrate der Steigung – positiv ist.
Noch einmal, hier ist f(x):
| f(x) | = | x2 – 6x + 5. |
| f ‚(x) | = | 2x – 6. |
| f “(x) | = | |
f “ ausgewertet am kritischen Wert 3 — f“(3) = 2 — ist positiv. Das sagt uns algebraisch, dass der kritische Wert 3 ein Minimum bestimmt.
Ausreichende Bedingungen

Wir können nun diese hinreichenden Bedingungen für Extremwerte einer Funktion an einem kritischen Wert a angeben:
Die Funktion hat einen minimalen Wert bei x = a, wenn f ‚(a) = 0
und f “(a) = eine positive Zahl ist.
Die Funktion hat einen Maximalwert bei x = a, wenn f ‚(a) = 0
und f “(a) = eine negative Zahl ist.
Im Fall des Maximums ist die Steigung der Tangente abnehmend – sie geht von positiv nach negativ. Wir können das an den Punkten C, A, D sehen.
Beispiel 2. Es sei f(x) = 2×3- 9×2 + 12x – 3.
Gibt es irgendwelche Extremwerte? Erstens: Gibt es kritische Werte – Lösungen von f ‚(x) = 0 – und bestimmen sie ein Maximum oder ein Minimum? Und was sind die Koördinaten auf dem Graphen dieses Maximums oder Minimums? Wo sind die Wendepunkte?
| Lösung. f ‚(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) |
| = | 6(x – 1)(x – 2) | |
| = | 0 | |
implies:
x = 1 oder x = 2.
(Lektion 37 der Algebra.)
Das sind die kritischen Werte. Bestimmt jeder von ihnen ein Maximum oder ein Minimum? Um das zu beantworten, müssen wir die zweite Ableitung bei jedem Wert auswerten.
| f ‚(x) | = | 6×2 – 18x + 12. |
| f “(x) | = | 12x – 18. |
| f “(1) | = | 12 – 18 = -6. |
Die zweite Ableitung ist negativ. Die Funktion hat also ein Maximum bei x = 1.
Um die y-Koordinate – den Extremwert – an diesem Maximum zu finden, werten wir f(1) aus:
| f(x) | = | 2×3- 9×2 + 12x – 3 |
| f(1) | = | 2 – 9 + 12 – 3 |
| = | ||
Das Maximum tritt am Punkt (1, 2).
Nächstes, bestimmt x = 2 ein Maximum oder ein Minimum?
| f “(x) | = | 12x – 18. |
| f “(2) | = | 24 – 18 = 6. |
Die zweite Ableitung ist positiv. Die Funktion hat also ein Minimum bei x = 2.
Um die y-Koordinate – den Extremwert – an diesem Minimum zu finden, werten wir f(2) aus:
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | = | 16 – 36 + 24 – 3 |
| = | ||
Das Minimum tritt am Punkt (2, 1).
Hier ist tatsächlich der Graph von f(x):
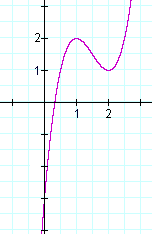
Lösungen zu f “(x) = 0 zeigen einen Wendepunkt bei diesen Lösungen, nicht ein Maximum oder Minimum. Ein Beispiel ist y = x3. y“ = 6x = 0 impliziert x = 0. Aber x = 0 ist ein Wendepunkt im Graphen von y = x3, nicht ein Maximum oder Minimum.
Ein anderes Beispiel ist y = sin x. Die Lösungen von y“ = 0 sind die Vielfachen von π, die Wendepunkte sind.
Problem 1. Finden Sie die Koördinaten des Scheitelpunkts der Parabel,
y = x2 – 8x + 1.
Um die Antwort zu sehen, fahren Sie mit der Maus über die farbige Fläche.
Um die Antwort wieder zu verdecken, klicken Sie auf „Aktualisieren“ („Reload“).
Lösen Sie die Aufgabe zuerst selbst!
y‘ = 2x – 8 = 0.
Das impliziert x = 4. Das ist die x-Kördinate des Scheitelpunkts. Um die y-Koordinate zu finden, werten Sie y bei x = 4 aus:
y = 42 – 8- 4 + 1 = -15.
Der Scheitelpunkt liegt bei (4, -15).
Aufgabe 2. Untersuchen Sie jede Funktion auf Maxima und Minima.
a) y = x3 – 3×2 + 2.
y‘ = 3×2 – 6x = 3x(x – 2) = 0 impliziert
x = 0 oder x = 2.
y“(x) = 6x – 6.
y“(0) = -6.
Die zweite Ableitung ist negativ. Das bedeutet, es gibt ein Maximum bei x = 0. Dieser Maximalwert ist
y(0) = 2.
Nächstes,
y“(2) = 12 – 6 = 6.
Die zweite Ableitung ist positiv. Das bedeutet, dass es ein Minimum bei x = 2 gibt. Dieser Minimalwert ist
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
Bei x = 1 gibt es ein Maximum von y = 17.
Bei x = -2 gibt es ein Minimum von y = -10.
c) y = 2×3 + 3×2 + 12 x – 4.
Da f ‚(x) = 0 keine reellen Lösungen hat, gibt es keine Extremwerte.