
An Approach
to
C A L C U L U S
Table of Contents | Home
グラフの転回点

ある関数f(x)がx=aで相対的に最大値を持つとします。
f(a)が直前または直後の任意の値よりも大きい場合。
これを「相対的な」最大値と呼ぶのは、関数の他の値が実際には大きいかもしれないからです。
関数f(x)はx = bにおいて相対的な最小値を持つと言うのは、
f(b)が直前または後続のどの値よりも小さい場合です。
さて、極値の時のグラフの特徴は何でしょうか?

曲線の接線は水平です。
f ‘(x) = 0.
さらに、最大値のすぐ左にある点Cでは、接線の傾きは正で、f ‘(x) > 0となります。 一方、すぐ右の点、つまり点Dでは、傾きは負の値:f ‘(x)
つまり、最大値では、f ‘(x)の符号が+から-に変わり、最小値では、f ‘(x)の符号が-から+に変わるということです。
また、最大値であるAでは、グラフは下向きに凹んでいることがわかります。
また、最大値となるAではグラフは下向きに凹み、最小値となるBでは上向きに凹むことがわかります(Precalculusのトピック14)。

–臨界値は x = a と x = b です。
臨界値によって、接線が x 軸に平行になる分岐点が決まります。
臨界値は、接線がx軸に平行になる分岐点を決定します。臨界値があれば、f ‘(x) = 0の解となります。
例1. f(x) = x2 – 6x + 5 とする。
臨界値 — 転換点はありますか? あるとすれば、それは最大または最小を決定するのでしょうか。
解答。 f ‘(x) = 2x – 6 = 0 implies x = 3. (代数学第9課)
x = 3が唯一の臨界値です。 それは転回点のx-共役である。 y座標を求めるには、その臨界値でfを評価します — f(3)を評価します。
| f(x) | = | x2 – 6x + 5 |
| f(3) | = | 32 – 6- 3 + 5 |
| = | -4. | |
極値は「-4」です。 最大値なのか最小値なのか、この場合は単純にグラフを見ればよいのですが、
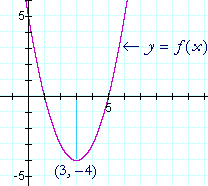
f(x)は放物線であり、転回点が最小値であることがわかります。
微分が0になるxの値を求めれば、放物線の頂点が(3, -4)にあることがわかります。
しかし、常にグラフを見ることができるわけではありません。 代数的な最小値の条件は、f ‘(x) の符号が – から + に変わることです。 これは上のE, B, Fの点で見られます。
さて、傾きが大きくなっているということは、臨界値において、2次微分(レッスン9)–傾きの変化率–が正であることを意味します。
再度、f(x)を見てみましょう:
| f(x) | = | x2 – 6x + 5. |
| f ‘(x) | = | 2x – 6. |
| f ”(x) | = | |
臨界値3で評価されるf ” — f”(3) = 2 — は正である。
充足条件

臨界値aにおける関数の極値の充足条件を以下に示します:
f ‘(a) = 0
かつf ”(a) = 正の数であるとき、関数はx = aにおいて極小値を持つ。
f ‘(a) = 0
and f ”(a) = 負の数の場合、関数は x = a で最大値を持ちます。
最大値の場合、接線の傾きは減少しています。
例2. f(x) = 2×3- 9×2 + 12x – 3とします。
極値はあるのでしょうか? まず、臨界値 (f ‘(x) = 0 の解) はあるのか、そしてそれは最大値や最小値を決めるのか。 また、その最大値または最小値のグラフ上の共線分は何ですか。
| 解。 f ‘(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) |
| = | 6(x – 1)(x – 2) | |
| = | 0 | |
インプリです。
x=1またはx=2である。
(代数学第37講。)
これらが臨界値です。 それぞれが最大値を決めるのか、最小値を決めるのか。
| f ‘(x) | = | 6×2 – 18x + 12. |
| f ”(x) | = | 12x – 18. |
| f ”(1) | = | 12 – 18 = -6. |
2次導関数は負の値をとります。 したがって、この関数はx = 1で最大となります。
その最大値でのy-cordinate(極値)を求めるために、f(1)を評価します。
| f(x) | = | 2×3- 9×2 + 12x – 3 |
| f(1) | = | 2 – 9 + 12 – 3 |
| = | ||
最大値が発生するのは、点(1, 2).
次に、x = 2で最大値と最小値のどちらが決まるでしょうか?
| f ”(x) | = | 12x – 18. |
| f ”(2) | = | |
2次導関数は正である。
この関数はx = 2に最小値を持ちます。
その最小値でのy-共役値(極値)を求めるために、f(2)を評価します:
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | = | 16 – 36 + 24 – 3 |
| = | ||
最小値は点(2.1)で発生します。 1).
実際にf(x)のグラフは以下の通りです:
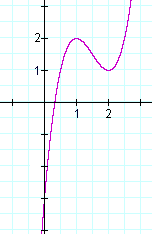
f ”(x)=0の解は、最大値や最小値ではなく、それらの解での変曲点を示しています。
もう一つの例はy = sin xです。y” = 0の解はπの倍数であり、これは変曲点です。
問題1. 放物線の頂点の共線を求めよ。
y = x2 – 8x + 1.
答えを見るには、色のついた部分にマウスを合わせます。
再度答えを表示するには、「更新」(「リロード」)をクリックします。
まずは自分で問題を解いてみましょう!
y’ = 2x – 8 = 0.
これは、x = 4を意味します。 これが頂点のx-共役です。
y = 42 – 8 – 4 + 1 = -15.
頂点は(4, -15)にあります。 各関数の最大値と最小値を調べよ。
a) y = x3 – 3×2 + 2.
y’ = 3×2 – 6x = 3x(x – 2) = 0 implies
x = 0 or x = 2.
y”(x) = 6x – 6.
y”(0) = -6.
二次導関数は負の値になります。 その最大値は
y(0)=2です。
次に、
y”(2) = 12 – 6 = 6.
二次導関数は正の値になります。 つまり、x = 2に最小値があるということです。 その最小値は
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
x = 1でy = 17の最大値があります。
x = -2においてy = -10の最小値があります。
c) y = 2×3 + 3×2 + 12 x – 4.
f ‘(x) = 0は実数解を持たないので、極値はありません
。