
Un approccio
a
C A L C U L U S
Indice | Home
I punti di svolta di un grafico

Si dice che una funzione f(x) ha un valore massimo relativo in x = a,
se f(a) è maggiore di qualsiasi valore immediatamente precedente o successivo.
Lo chiamiamo un massimo “relativo” perché altri valori della funzione possono in effetti essere maggiori.
Diciamo che una funzione f(x) ha un valore minimo relativo a x = b,
se f(b) è minore di qualsiasi valore immediatamente precedente o successivo.
Ancora una volta, altri valori della funzione possono in effetti essere minori. Con questa comprensione, quindi, lasceremo cadere il termine relativo.
Il valore della funzione, il valore di y, sia ad un massimo che ad un minimo è chiamato valore estremo.
Ora, cosa caratterizza il grafico ad un valore estremo?

La tangente alla curva è orizzontale. Lo vediamo nei punti A e B. La pendenza di ogni linea tangente – la derivata valutata in a o in b – è 0.
f ‘(x) = 0.
Inoltre, nei punti immediatamente a sinistra di un massimo – nel punto C – la pendenza della tangente è positiva: f ‘(x) > 0. Mentre nei punti immediatamente a destra — in un punto D — la pendenza è negativa: f ‘(x)
In altre parole, in un massimo, f ‘(x) cambia segno da + a – .
In un minimo, f ‘(x) cambia segno da – a + . Possiamo vedere che nei punti E e F.
Si può anche osservare che in un massimo, in A, il grafico è concavo verso il basso. (Argomento 14 del Precalculus.) Mentre ad un minimo, in B, è concavo verso l’alto.
Un valore di x in cui la funzione ha un massimo o un minimo è chiamato valore critico. Nella figura —

— i valori critici sono x = a e x = b.
I valori critici determinano punti di svolta, in cui la tangente è parallela all’asse x. I valori critici – se ci sono – saranno le soluzioni di f ‘(x) = 0.
Esempio 1. Sia f(x) = x2 – 6x + 5.
Ci sono dei valori critici — dei punti di svolta? Se sì, determinano un massimo o un minimo? E quali sono le coordinate sul grafico di quel massimo o minimo?
Soluzione. f ‘(x) = 2x – 6 = 0 implica x = 3. (Lezione 9 di Algebra.)
x = 3 è l’unico valore critico. È la coordina x del punto di svolta. Per determinare il codominio y, valuta f a quel valore critico – valuta f(3):
| f(x) | = | x2 – 6x + 5 | |
| f(3) | = | 32 – 6- 3 + 5 | |
| = | -4. | ||
Il valore estremo è -4. Per vedere se è un massimo o un minimo, in questo caso possiamo semplicemente guardare il grafico.
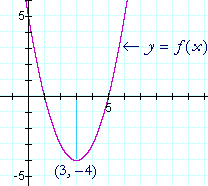
f(x) è una parabola, e possiamo vedere che il punto di svolta è un minimo.
Trovando il valore di x dove la derivata è 0, quindi, abbiamo scoperto che il vertice della parabola è a (3, -4).
Ma non potremo sempre guardare il grafico. La condizione algebrica per un minimo è che f ‘(x) cambia segno da – a + . Lo vediamo nei punti E, B, F qui sopra. Il valore della pendenza è crescente.
Ora dire che la pendenza è crescente, è come dire che, ad un valore critico, la derivata seconda (Lezione 9) — che è il tasso di cambiamento della pendenza — è positiva.
Di nuovo, ecco f(x):
| f(x) | = | x2 – 6x + 5. |
| f ‘(x) | = | 2x – 6. |
| f ”(x) | = | |
f ” valutata al valore critico 3 — f”(3) = 2 — è positiva. Questo ci dice algebricamente che il valore critico 3 determina un minimo.
Condizioni sufficienti

Possiamo ora enunciare queste condizioni sufficienti per i valori estremi di una funzione in un valore critico a:
La funzione ha un valore minimo in x = a se f ‘(a) = 0
e f ”(a) = un numero positivo.
La funzione ha un valore massimo in x = a se f ‘(a) = 0
e f ”(a) = un numero negativo.
Nel caso del massimo, la pendenza della tangente è decrescente — va da positivo a negativo. Possiamo vedere che nei punti C, A, D.
Esempio 2. Sia f(x) = 2×3- 9×2 + 12x – 3.
Ci sono valori estremi? Innanzitutto, ci sono valori critici – soluzioni di f ‘(x) = 0 – e determinano un massimo o un minimo? E quali sono le coordinate sul grafico di quel massimo o minimo? Dove sono i punti di svolta?
| Soluzione. f ‘(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) | |
| = | 6(x – 1)(x – 2) | ||
| = | 0 | ||
implica:
x = 1 o x = 2.
(Lezione 37 di Algebra.)
Questi sono i valori critici. Ognuno di essi determina un massimo o determina un minimo? Per rispondere, dobbiamo valutare la derivata seconda ad ogni valore.
| f ‘(x) | = | 6×2 – 18x + 12. |
| f ”(x) | = | 12x – 18. |
| f ”(1) | = | 12 – 18 = -6. |
La derivata seconda è negativa. La funzione ha quindi un massimo in x = 1.
Per trovare il codominio y — il valore estremo — in quel massimo valutiamo f(1):
| f(x) | = | 2×3- 9×2 + 12x – 3 | |
| f(1) | = | 2 – 9 + 12 – 3 | |
| = | |||
Il massimo avviene nel punto (1, 2).
Prossimo, x = 2 determina un massimo o un minimo?
| f ”(x) | = | 12x – 18. |
| f ”(2) | = | 24 – 18 = 6. |
La derivata seconda è positiva. La funzione ha quindi un minimo in x = 2.
Per trovare il coordine y — il valore estremo — in quel minimo, valutiamo f(2):
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | = | 16 – 36 + 24 – 3 |
| = | ||
Il minimo avviene nel punto (2, 1).
Ecco infatti il grafico di f(x):
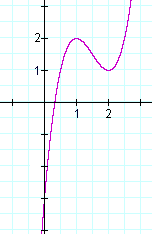
Le soluzioni a f ”(x) = 0 indicano un punto di flesso a quelle soluzioni, non un massimo o un minimo. Un esempio è y = x3. y” = 6x = 0 implica x = 0. Ma x = 0 è un punto di flesso nel grafico di y = x3, non un massimo o un minimo.
Un altro esempio è y = sin x. Le soluzioni a y” = 0 sono i multipli di π, che sono punti di flesso.
Problema 1. Trova le coordinate del vertice della parabola,
y = x2 – 8x + 1.
Per vedere la risposta, passa il mouse sull’area colorata.
Per coprire di nuovo la risposta, clicca su “Refresh” (“Ricarica”).
Fai prima tu il problema!
y’ = 2x – 8 = 0.
Questo implica x = 4. Questa è la coordina x del vertice. Per trovare il codominio y, valutare y in x = 4:
y = 42 – 8- 4 + 1 = -15.
Il vertice è a (4, -15).
Problema 2. Esaminare ogni funzione per massimi e minimi.
a) y = x3 – 3×2 + 2.
y’ = 3×2 – 6x = 3x(x – 2) = 0 implica
x = 0 o x = 2.
y”(x) = 6x – 6.
y”(0) = -6.
La derivata seconda è negativa. Questo significa che c’è un massimo a x = 0. Questo valore massimo è
y(0) = 2.
Avanti,
y”(2) = 12 – 6 = 6.
La derivata seconda è positiva. Questo significa che c’è un minimo a x = 2. Questo valore minimo è
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
A x = 1 c’è un massimo di y = 17.
A x = -2 c’è un minimo di y = -10.
c) y = 2×3 + 3×2 + 12 x – 4.
Siccome f ‘(x) = 0 non ha soluzioni reali, non esistono valori estremi.