Valeurs maximales et minimales

Les points d’inflexion d’un graphique

On dit qu’une FONCTION f(x) a une valeur maximale relative en x = a,
si f(a) est supérieure à toute valeur qui la précède ou la suit immédiatement.

Nous l’appelons un maximum « relatif » parce que d’autres valeurs de la fonction peuvent en fait être plus grandes.

Nous disons qu’une fonction f(x) a une valeur minimale relative à x = b,
si f(b) est inférieure à toute valeur précédant ou suivant immédiatement.

Encore, d’autres valeurs de la fonction peuvent en fait être inférieures. Avec cette compréhension, nous laisserons donc tomber le terme relatif.

La valeur de la fonction, la valeur de y, à un maximum ou à un minimum est appelée une valeur extrême.

Maintenant, qu’est-ce qui caractérise le graphique à une valeur extrême ?

La tangente à la courbe est horizontale. Nous le voyons aux points A et B. La pente de chaque ligne tangente — la dérivée lorsqu’elle est évaluée en a ou en b — est 0.

f ‘(x) = 0.

De plus, aux points immédiatement à gauche d’un maximum — en un point C — la pente de la tangente est positive : f ‘(x) > 0. Alors qu’aux points immédiatement à droite — en un point D — la pente est négative : f ‘(x)

En d’autres termes, à un maximum, f ‘(x) change de signe de + à – .

À un minimum, f ‘(x) change de signe de – à + . On peut voir cela aux points E et F.

On peut aussi observer qu’à un maximum, en A, le graphique est concave vers le bas. (Sujet 14 du Précalcul.) Tandis qu’à un minimum, en B, il est concave vers le haut.

Une valeur de x pour laquelle la fonction a soit un maximum, soit un minimum est appelée valeur critique. Dans la figure —

— les valeurs critiques sont x = a et x = b.

Les valeurs critiques déterminent des points de retournement, auxquels la tangente est parallèle à l’axe des x. Les valeurs critiques — si elles existent — seront les solutions de f ‘(x) = 0.

Exemple 1. Soit f(x) = x2 – 6x + 5.

Y a-t-il des valeurs critiques — des points d’inflexion ? Si oui, déterminent-ils un maximum ou un minimum ? Et quels sont les coördinats sur le graphique de ce maximum ou de ce minimum ?

Solution. f ‘(x) = 2x – 6 = 0 implique x = 3. (Leçon 9 d’algèbre.)

x = 3 est la seule valeur critique. C’est la coördinate en x du point d’inflexion. Pour déterminer l’y-coördinate, évaluez f à cette valeur critique — évaluez f(3) :

.

	f(x)	=	x2 – 6x + 5
f(3)	=	32 – 6- 3 + 5
	=	-4.

La valeur extrême est -4. Pour savoir s’il s’agit d’un maximum ou d’un minimum, il suffit dans ce cas de regarder le graphique.

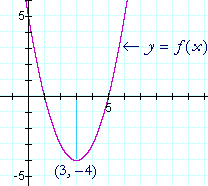
f(x) est une parabole, et on peut voir que le point d’inflexion est un minimum.

En trouvant la valeur de x où la dérivée est 0, nous avons donc découvert que le sommet de la parabole est à (3, -4).

Mais nous ne pourrons pas toujours regarder le graphique. La condition algébrique d’un minimum est que f ‘(x) change de signe de – à + . Nous voyons cela aux points E, B, F ci-dessus. La valeur de la pente est croissante.

Maintenant, dire que la pente est croissante, c’est dire que, à une valeur critique, la dérivée seconde (leçon 9) — qui est le taux de variation de la pente — est positive.

A nouveau, voici f(x):

f(x)	=	x2 – 6x + 5.
f ‘(x)	=	2x – 6.
f  »(x)	=

f  » évaluée à la valeur critique 3 — f »(3) = 2 — est positive. Cela nous indique algébriquement que la valeur critique 3 détermine un minimum.

Conditions suffisantes

Nous pouvons maintenant énoncer ces conditions suffisantes pour les valeurs extrêmes d’une fonction à une valeur critique a :

La fonction a une valeur minimale en x = a si f ‘(a) = 0 et f  »(a) = un nombre positif.

La fonction a une valeur maximale en x = a si f ‘(a) = 0
et f  »(a) = un nombre négatif.

Dans le cas du maximum, la pente de la tangente est décroissante — elle passe du positif au négatif. On peut voir cela aux points C, A, D.

Exemple 2. Soit f(x) = 2×3- 9×2 + 12x – 3.

Y a-t-il des valeurs extrêmes ? Tout d’abord, existe-t-il des valeurs critiques — solutions de f ‘(x) = 0 — et déterminent-elles un maximum ou un minimum ? Et quels sont les coördinats sur le graphique de ce maximum ou de ce minimum ? Où sont les points de retournement ?

Solution. f ‘(x) = 6×2 – 18x + 12	=	6(x2 – 3x + 2)
		=	6(x – 1)(x – 2)
	=	0

implique :

x = 1 ou x = 2.

(Leçon 37 d’algèbre.)

Ce sont les valeurs critiques. Chacune d’entre elles détermine-t-elle un maximum ou un minimum ? Pour répondre, nous devons évaluer la dérivée seconde à chaque valeur.

f ‘(x)	=	6×2 – 18x + 12.
f  »(x)	=	12x – 18.
f  »(1)	=	12 – 18 = -6.

La dérivée seconde est négative. La fonction a donc un maximum en x = 1.

Pour trouver l’y-coördinate — la valeur extrême — à ce maximum, on évalue f(1) :

	f(x)	=	2×3- 9×2 + 12x – 3
	f(1)	=	. 2 – 9 + 12 – 3
=

Le maximum se produit au point (1, 2).

Après, x = 2 détermine-t-il un maximum ou un minimum ?

f  »(x)	=	12x – 18.
f  »(2)	=	24 – 18 = 6.

La dérivée seconde est positive. La fonction a donc un minimum à x = 2.

Pour trouver le y-coördinate — la valeur extrême — à ce minimum, on évalue f(2) :

f(x)	=	2×3 – 9×2 + 12x – 3.
f(2)	=	16 – 36 + 24 – 3
.
	=

Le minimum se produit au point (2, 1).

Voici en fait le graphe de f(x):

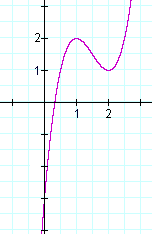
Les solutions de f  »(x) = 0 indiquent un point d’inflexion à ces solutions, et non un maximum ou un minimum. Un exemple est y = x3. y » = 6x = 0 implique x = 0. Mais x = 0 est un point d’inflexion dans le graphique de y = x3, pas un maximum ou un minimum.

Un autre exemple est y = sin x. Les solutions de y » = 0 sont les multiplications de π, qui sont des points d’inflexion.

Problème 1. Trouvez les coördinats du sommet de la parabole,

y = x2 – 8x + 1.

Pour voir la réponse, passez votre souris sur la zone colorée.
Pour recouvrir la réponse, cliquez sur « Rafraîchir » (« Reload »).
Faites d’abord le problème vous-même !

y’ = 2x – 8 = 0.

Cela implique que x = 4. C’est le coördinat x du sommet. Pour trouver le coördinat de y, évaluez y à x = 4 :

y = 42 – 8- 4 + 1 = -15.

Le sommet est à (4, -15).

Problème 2. Examinez les maxima et les minima de chaque fonction.

a) y = x3 – 3×2 + 2.

y’ = 3×2 – 6x = 3x(x – 2) = 0 implique

x = 0 ou x = 2.

y »(x) = 6x – 6.

y »(0) = -6.

La dérivée seconde est négative. Cela signifie qu’il existe un maximum à x = 0. Cette valeur maximale est

y(0) = 2.

Suivant,

y »(2) = 12 – 6 = 6.

La dérivée seconde est positive. Cela signifie qu’il existe un minimum à x = 2. Cette valeur minimale est

y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.

b) y = -2×3 – 3×2 + 12 x + 10.

À x = 1, il y a un maximum de y = 17.

Au niveau de x = -2, il y a un minimum de y = -10.

c) y = 2×3 + 3×2 + 12 x – 4.

Puisque f ‘(x) = 0 n’a pas de solutions réelles, il n’y a pas de valeurs extrêmes.