
Una aproximación
a
C A L C U L U S
Tabla de contenidos | Inicio
Los puntos de inflexión de una gráfica

DECIMOS QUE UNA FUNCIÓN f(x) tiene un valor máximo relativo en x = a,
si f(a) es mayor que cualquier valor inmediatamente anterior o posterior.
Lo llamamos máximo «relativo» porque otros valores de la función pueden ser, de hecho, mayores.
Decimos que una función f(x) tiene un valor mínimo relativo en x = b,
si f(b) es menor que cualquier valor inmediatamente anterior o posterior.
De nuevo, otros valores de la función pueden ser, de hecho, menores. Entendiendo esto, entonces, dejaremos de lado el término relativo.
El valor de la función, el valor de y, en un máximo o en un mínimo se llama valor extremo.
Ahora, ¿qué caracteriza a la gráfica en un valor extremo?

La tangente a la curva es horizontal. Lo vemos en los puntos A y B. La pendiente de cada recta tangente — la derivada cuando se evalúa en a o b — es 0.
f ‘(x) = 0.
Además, en los puntos inmediatamente a la izquierda de un máximo — en un punto C — la pendiente de la tangente es positiva: f ‘(x) > 0. Mientras que en los puntos inmediatamente a la derecha — en un punto D — la pendiente es negativa: f ‘(x)
En otras palabras, en un máximo, f ‘(x) cambia de signo de + a – .
En un mínimo, f ‘(x) cambia de signo de – a + . Podemos ver que en los puntos E y F.
También podemos observar que en un máximo, en A, la gráfica es cóncava hacia abajo. (Tema 14 de Precálculo.) Mientras que en un mínimo, en B, es cóncava hacia arriba.
Un valor de x en el que la función tiene un máximo o un mínimo se llama valor crítico. En la figura —

— los valores críticos son x = a y x = b.
Los valores críticos determinan puntos de inflexión, en los que la tangente es paralela al eje x. Los valores críticos — si los hay — serán las soluciones de f ‘(x) = 0.
Ejemplo 1. Sea f(x) = x2 – 6x + 5.
¿Hay algún valor crítico — algún punto de inflexión? Si es así, ¿determinan un máximo o un mínimo? Y ¿cuáles son las coördinadas en la gráfica de ese máximo o mínimo?
Solución. f ‘(x) = 2x – 6 = 0 implica x = 3. (Lección 9 de Álgebra.)
x = 3 es el único valor crítico. Es la coordenada x del punto de inflexión. Para determinar la coordenada y, evalúa f en ese valor crítico — evalúa f(3):
| f(x) | = | x2 – 6x + 5 |
| f(3) | = | 32 – 6- 3 + 5 |
| = | -4. | |
El valor extremo es -4. Para ver si es un máximo o un mínimo, en este caso podemos simplemente mirar la gráfica.
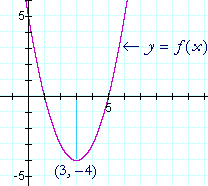
f(x) es una parábola, y podemos ver que el punto de inflexión es un mínimo.
Al encontrar el valor de x donde la derivada es 0, entonces, hemos descubierto que el vértice de la parábola está en (3, -4).
Pero no siempre podremos mirar la gráfica. La condición algebraica para un mínimo es que f ‘(x) cambie de signo de – a + . Esto lo vemos en los puntos E, B, F anteriores. El valor de la pendiente es creciente.
Ahora, decir que la pendiente es creciente, es decir que, en un valor crítico, la segunda derivada (Lección 9) — que es tasa de cambio de la pendiente — es positiva.
De nuevo, aquí está f(x):
| f(x) | = | x2 – 6x + 5. |
| f ‘(x) | = | 2x – 6. |
| f »(x) | = | |
f » evaluada en el valor crítico 3 — f»(3) = 2 — es positiva. Esto nos dice algebraicamente que el valor crítico 3 determina un mínimo.
Condiciones suficientes

Ahora podemos enunciar estas condiciones suficientes para los valores extremos de una función en un valor crítico a:
La función tiene un valor mínimo en x = a si f ‘(a) = 0
y f »(a) = un número positivo.
La función tiene un valor máximo en x = a si f ‘(a) = 0
y f »(a) = un número negativo.
En el caso del máximo, la pendiente de la tangente es decreciente — va de positiva a negativa. Podemos verlo en los puntos C, A, D.
Ejemplo 2. Sea f(x) = 2×3- 9×2 + 12x – 3.
¿Hay algún valor extremo? En primer lugar, ¿existen valores críticos -soluciones de f ‘(x) = 0- y determinan un máximo o un mínimo? Y ¿cuáles son las coördinadas en la gráfica de ese máximo o mínimo? ¿Dónde están los puntos de inflexión?
| Solución. f ‘(x) = 6×2 – 18x + 12 | = | 6(x2 – 3x + 2) |
| 6(x – 1)(x – 2) | ||
| = | 0 | |
implica:
x = 1 o x = 2.
(Lección 37 de Álgebra.)
Esos son los valores críticos. Cada uno determina un máximo o determina un mínimo? Para responder, debemos evaluar la segunda derivada en cada valor.
| f ‘(x) | = | 6×2 – 18x + 12. |
| f »(x) | = | 12x – 18. |
| f »(1) | = | 12 – 18 = -6. |
La segunda derivada es negativa. Por tanto, la función tiene un máximo en x = 1.
Para encontrar la coordenada y –el valor extremo– en ese máximo evaluamos f(1):
| f(x) | = | 2×3- 9×2 + 12x – 3 |
| f(1) | = | 2 – 9 + 12 – 3 |
| = | = | |
El máximo se produce en el punto (1, 2).
A continuación, ¿determina x = 2 un máximo o un mínimo?
| f »(x) | = | 12x – 18. |
| f »(2) | = | 24 – 18 = 6. |
La segunda derivada es positiva. Por tanto, la función tiene un mínimo en x = 2.
Para encontrar la coordenada y –el valor extremo– en ese mínimo, evaluamos f(2):
| f(x) | = | 2×3 – 9×2 + 12x – 3. |
| f(2) | = | 16 – 36 + 24 – 3 |
| . | ||
| = | ||
El mínimo se produce en el punto (2, 1).
Aquí está, de hecho, la gráfica de f(x):
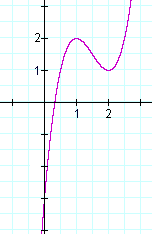
Las soluciones de f »(x) = 0 indican un punto de inflexión en esas soluciones, no un máximo o un mínimo. Un ejemplo es y = x3. y» = 6x = 0 implica que x = 0. Pero x = 0 es un punto de inflexión en la gráfica de y = x3, no un máximo o un mínimo.
Otro ejemplo es y = sen x. Las soluciones de y» = 0 son los múltiplos de π, que son puntos de inflexión.
Problema 1. Encuentra las coördinadas del vértice de la parábola,
y = x2 – 8x + 1.
Para ver la respuesta, pasa el ratón por la zona coloreada.
Para volver a cubrir la respuesta, haz clic en «Actualizar» («Reload»).
¡Haz el problema tú primero!
y’ = 2x – 8 = 0.
Eso implica que x = 4. Esa es la coordenada x del vértice. Para encontrar la coordenada y, evalúa y en x = 4:
y = 42 – 8- 4 + 1 = -15.
El vértice está en (4, -15).
Problema 2. Examina cada función en busca de máximos y mínimos.
a) y = x3 – 3×2 + 2.
y’ = 3×2 – 6x = 3x(x – 2) = 0 implica
x = 0 o x = 2.
y»(x) = 6x – 6.
y»(0) = -6.
La segunda derivada es negativa. Eso significa que hay un máximo en x = 0. Ese valor máximo es
y(0) = 2.
Siguiente,
y»(2) = 12 – 6 = 6.
La segunda derivada es positiva. Eso significa que hay un mínimo en x = 2. Ese valor mínimo es
y(2) = 23 – 3- 22 + 2 = 8 – 12 + 2 = -2.
b) y = -2×3 – 3×2 + 12 x + 10.
En x = 1 hay un máximo de y = 17.
En x = -2 hay un mínimo de y = -10.
c) y = 2×3 + 3×2 + 12 x – 4.
Como f ‘(x) = 0 no tiene soluciones reales, no hay valores extremos.