Ein Verhältnis vergleicht Werte.
Ein Verhältnis sagt aus, wie viel von einer Sache im Vergleich zu einer anderen Sache vorhanden ist.

Es gibt 3 blaue Quadrate zu 1 gelbes Quadrat
Verhältnisse können auf verschiedene Weise dargestellt werden:
| Verwenden Sie das „:“, um die Werte zu trennen: | 3 : 1 | |
| Oder wir können das Wort „bis“ verwenden: | 3 zu 1 | |
| Oder wir schreiben es wie einen Bruch: | 31 |
Ein Verhältnis kann skaliert werden:
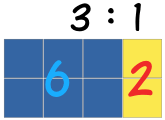
Hier ist das Verhältnis ebenfalls 3 blaue Quadrate zu 1 gelbes Quadrat,
auch wenn es mehr Quadrate gibt.
Verwendung von Verhältnissen
Der Trick bei Verhältnissen ist, die Zahlen immer mit dem gleichen Wert zu multiplizieren oder zu dividieren.
Beispiel:
|
4 : 5 ist das gleiche wie 4×2 : 5×2 = 8 : 10 |
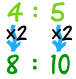 |
Rezepte
Beispiel: In einem Rezept für Pfannkuchen werden 3 Tassen Mehl und 2 Tassen Milch verwendet.
Das Verhältnis von Mehl zu Milch ist also 3 : 2
Um Pfannkuchen für viele Leute zu machen, brauchen wir vielleicht die 4-fache Menge, also multiplizieren wir die Zahlen mit 4:
3×4 : 2×4 = 12 : 8
Mit anderen Worten, 12 Tassen Mehl und 8 Tassen Milch.
Das Verhältnis ist immer noch dasselbe, also sollten die Pfannkuchen genauso lecker sein.
„Teil-zu-Teil“- und „Teil-zu-Ganzem“-Verhältnisse
Die bisherigen Beispiele waren „Teil-zu-Teil“-Verhältnisse (ein Teil wird mit einem anderen Teil verglichen).
Aber ein Verhältnis kann auch einen Teil im Vergleich zum Ganzen zeigen.
Beispiel: Es gibt 5 Welpen, 2 sind Jungen und 3 sind Mädchen

Teil zu Teil:
Das Verhältnis von Jungen zu Mädchen ist 2:3 oder 2/3
Das Verhältnis von Mädchen zu Jungen ist 3:2 oder 3/2
Teil zu Ganzem:
Das Verhältnis von Jungen zu allen Welpen ist 2:5 oder 2/5
Das Verhältnis von Mädchen zu allen Welpen ist 3:5 oder 3/5
Versuchen Sie es selbst
Wir können Verhältnisse verwenden, um Zeichnungen nach oben oder unten zu skalieren (durch Multiplizieren oder Dividieren).
|
Das Verhältnis von Höhe zu Breite der indischen Flagge ist 2:3 Also für jede 2 (Zoll, Meter, was auch immer) der Höhe |
 |
|
Wenn wir die Flagge 20 Zoll hoch machen, sollte sie 30 Zoll breit sein. Wenn wir die Flagge 40 cm hoch machen, sollte sie 60 cm breit sein (was immer noch im Verhältnis 2:3 ist) |
|
Beispiel: Um ein Pferd in 1/10 Normalgröße zu zeichnen, multiplizieren Sie alle Größen mit 1/10
Dieses Pferd ist im realen Leben 1500 mm hoch und 2000 mm lang, also ist das Verhältnis von Höhe zu Länge
1500 : 2000
Wie ist dieses Verhältnis, wenn wir es in 1/10 der normalen Größe zeichnen?
| 1500 : 2000 | = 1500×1/10 : 2000×1/10 | |
| = 150 : 200 |
Auf diese Weise können wir jede gewünschte Verkleinerung/Vergrößerung vornehmen.
Großer Fuß?
 |
Allie hat ihren Fuß gemessen und er war 21cm lang, und dann hat sie den Fuß ihrer Mutter gemessen und er war 24cm lang. |
„Ich muss große Füße haben, mein Fuß ist fast so lang wie der von meiner Mutter!“
Aber dann dachte sie daran, die Höhe zu messen, und stellte fest, dass sie 133 cm groß ist und ihre Mama 152 cm.
In einer Tabelle ist das:
| Allie | Mom | Fußlänge: | 21cm | 24cm |
| Höhe: | 133cm | 152cm |
Das Verhältnis von „Fuß zu Höhe“ im Fraktionsstil ist:
| Allie: | 21133 | Mom: | 24152 |
Das Verhältnis für Allie ist also 21 : 133
Es ist immer noch das gleiche Verhältnis, richtig? Weil wir beide Zahlen durch den gleichen Betrag geteilt haben.
Und das Verhältnis für Mama ist 24 : 152
Dieses Mal haben wir durch 8 geteilt, aber auch dieses Verhältnis bleibt gleich.
Die vereinfachten „Fuß-zu-Höhe“-Verhältnisse sind nun:
| Allie: | 319 | Mom: | 319 |
„Oh!“, sagte sie, „die Verhältnisse sind gleich“.
„Also ist mein Fuß nur so groß, wie er für meine Größe sein sollte, und nicht wirklich zu groß.“
