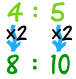A razão compara valores.
A razão diz quanto de uma coisa há em comparação com outra coisa.
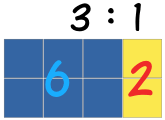
 br>Há 3 quadrados azuis para 1 quadrado amarelo
br>Há 3 quadrados azuis para 1 quadrado amarelo
Ratios podem ser mostrados de diferentes maneiras:
| Utilizar o “:” para separar os valores: | |
| Sou podemos usar a palavra “para”: | 3 a 1 |
| Or escreva-a como uma fracção: |
Uma proporção pode ser aumentada:
 br>>Aqui é também 3 quadrados azuis para 1 quadrado amarelo,
br>>Aqui é também 3 quadrados azuis para 1 quadrado amarelo,
mesmo que haja mais quadrados.
Rácios de utilização
O truque com os rácios é sempre multiplicar ou dividir os números pelo mesmo valor.
Exemplo:
| p>4 : 5 é o mesmo que 4×2 : 5×2 = 8 : 10 |
Recipes
Exemplo: Uma receita para panquecas usa 3 chávenas de farinha e 2 chávenas de leite.
Por isso a proporção de farinha para leite é 3 : 2
Para fazer panquecas para um LOT de pessoas podemos precisar de 4 vezes a quantidade, por isso multiplicamos os números por 4:
3×4 : 2×4 = 12 : 8
Por outras palavras, 12 chávenas de farinha e 8 chávenas de leite.
A proporção ainda é a mesma, por isso as panquecas devem ser igualmente saborosas.
Razões “Part-to-Part” e “Part-to-Whole”
Os exemplos até agora têm sido “part-to-part” (comparando uma parte com outra parte).
Mas uma proporção também pode mostrar uma parte em comparação com o lote inteiro.
Exemplo: Há 5 cachorros, 2 são rapazes, e 3 são raparigas

Parte-a-parte:
A proporção de rapazes para raparigas é 2:3 ou 2/3
A proporção de raparigas para rapazes é 3:2 ou 3/2
Parte-parte-parte:
A proporção de rapazes para todos os cachorros é 2:5 ou 2/5
A proporção de raparigas para todos os cachorros é 3:5 ou 3/5
Try It Yourself
Podemos usar rácios para escalar desenhos para cima ou para baixo (multiplicando ou dividindo).
|
a relação altura/largura da Bandeira Indiana é 2:3 por isso, para cada 2 (polegadas, metros, o que quer que seja) de altura |
 |
Exemplo: Para desenhar um cavalo a 1/10º tamanho normal, multiplique todos os tamanhos por 1/10º
Este cavalo na vida real tem 1500 mm de altura e 2000 mm de comprimento, pelo que a razão entre a sua altura e o seu comprimento é
1500 : 2000
Qual é essa relação quando o desenhamos a 1/10º do seu tamanho normal?
| 1500 : 2000 | = 1500×1/10 : 2000×1/10 |
Podemos fazer qualquer redução/alargamento que quisermos dessa forma.
Big Foot?
 |
Allie mediu o pé e este tinha 21cm de comprimento, e depois mediu o pé da mãe, e tinha 24cm de comprimento. |
“Devo ter pés grandes, o meu pé é quase tão comprido como o da minha mãe!”
Mas depois ela pensou em medir alturas, e descobriu que tinha 133cm de altura, e que a sua mãe tinha 152cm de altura.
Em uma mesa isto é:
| Allie | Mãe | |
| Comprimento do pé: | 21cm | 24cm |
| Altura: | 133cm | 152cm |
A relação “pé/altura” em estilo de fracção é:
| Allie: | 21133 | 24152 |
Então a proporção para Allie é 21 : 133
Ainda é a mesma proporção, certo? Porque dividimos ambos os números pelo mesmo valor.
E a proporção para a mãe é 24 : 152
Desta vez dividimos por 8, mas essa proporção também permanece a mesma.
As razões simplificadas de “pé para altura” são agora:
| Allie: | 319 | 319 |
“Oh!” disse ela, “os rácios são os mesmos”.
“Por isso o meu pé é tão grande como deveria ser para a minha altura, e não é realmente muito grande”.