p> Este artigo fazia parte de um projecto que executámos para celebrar o Ano Internacional da Astronomia 2009. O projecto pediu-lhe para nomear as perguntas sobre o Universo que mais gostaria de ter respondido, e esta é uma delas. Levámo-lo ao físico Nicholas Mee e aqui está a sua resposta.
Quanto tempo é um dia? Quanto tempo leva a Terra a girar uma vez no seu eixo?
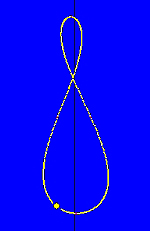
Qual é esta figura estranha? Continuar a ler…
Pode parecer óbvio que a resposta a estas duas perguntas é 24 horas. Mas a resposta correcta não é tão directa. O eixo da Terra aponta sempre na mesma direcção em relação às estrelas distantes, pelo menos para uma boa aproximação. Esta direcção está próxima da direcção em direcção à estrela que conhecemos como Polaris. De facto, a Terra demora um pouco mais de 23 horas e 56 minutos a rodar uma vez em torno deste eixo. Neste tempo, todas as estrelas parecem girar uma vez em torno da Terra e regressar às suas posições iniciais. Os astrónomos chamam a este período de tempo um dia sideral. A palavra “sidereal” deriva da palavra latina “sidereus”, que significa estrela.
Sem sermos astrónomos e preocupando-nos com as posições das estrelas no céu nocturno, preferimos medir o tempo em relação à posição do Sol. Definimos um dia para ser o período de tempo entre aparições consecutivas do Sol para sul no céu.
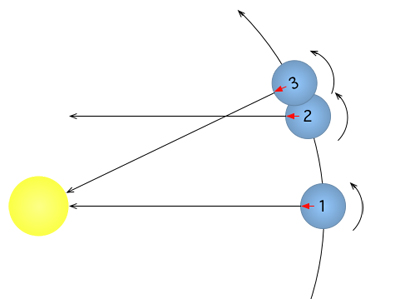
O dia sideral é mais curto do que o dia solar: no momento 1 o Sol está directamente sobre o seu eixo. No momento 2, a Terra rodou uma vez sobre o seu eixo, mas o Sol ainda não está directamente sobre a superfície. Temos de esperar mais 1/366 de uma rotação completa até que o Sol esteja. Imagem cortesia Gdr.
A Terra não está apenas a girar sobre o seu eixo, está simultaneamente a orbitar o Sol. No período de tempo que leva a girar uma vez, terá também viajado cerca de 1/366 do caminho em torno da sua órbita. Isto significa que uma rotação completa da Terra não trará o Sol de volta ao seu ponto de partida no céu, teremos de esperar que a Terra gire para mais 1/366 de uma rotação completa. Este período de tempo é de cerca de 24 horas dividido por 366, que é de cerca de 24 × 60/360 minutos – quase exactamente quatro minutos. E estes quatro minutos adicionais dão-nos o nosso dia de 24 horas. É o tempo entre o Sol estar a ir para sul no céu e voltar de novo exactamente na mesma direcção em direcção a sul.
Viagem rápida entre lugares distantes tornou-se viável pela primeira vez na era Vitoriana. Isto significava que agora era necessário comparar o tempo num lugar do globo terrestre com o tempo em outros lugares. Já não era prático que o tempo fosse determinado localmente pela posição do Sol em todo o mundo. Por exemplo, haveria uma diferença de dez minutos entre a hora local em Londres e a hora local em Bristol, a apenas 120 milhas de distância; uma distância que poderia ter sido percorrida por comboio em menos de duas horas em meados do século XIX. Por uma convenção internacional de 1884, o Observatório Real de Greenwich, nos arredores da Capital Imperial Britânica de Londres, foi estabelecido como o local em que a hora seria fixada para todo o mundo. Quando o Sol está previsto para sul, em Greenwich, são doze horas do meio-dia, o que marca a hora para o resto do mundo. A Hora Média de Greenwich, ou GMT, tornou-se o padrão para a definição de relógios em todo o lado.
Isto contabiliza o G e o T no GMT, mas e quanto ao M? Bem, o movimento da Terra à volta do Sol não é tão simples como sugerimos acima. Se o eixo da Terra fosse perpendicular ao plano da órbita da Terra em torno do Sol e a órbita da Terra fosse um círculo perfeito, então a nossa explicação estaria de facto exactamente correcta. Mas o eixo da Terra está inclinado a um ângulo de cerca de 23,5° da perpendicular ao plano da órbita da Terra. E embora a órbita da Terra esteja perto de ser circular, na realidade é uma elipse, por isso tem a forma de um círculo ligeiramente esmagado.
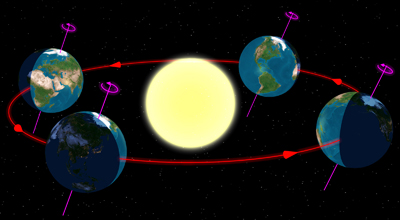
A órbita da Terra é elíptica e o eixo da Terra é inclinado em relação ao plano orbital. Imagem cortesia Tau’olunga.
Estes dois factores significam que o tempo necessário para o Sol regressar a uma posição devida a sul no céu varia ligeiramente ao longo do ano. Em média, este período de tempo é de 24 horas. Mas em algumas alturas do ano é ligeiramente mais longo e noutras do ano é ligeiramente mais curto. O nome Greenwich Mean Time (Tempo Médio de Greenwich) é exactamente o que sugere. É o tempo médio ao longo do ano, de modo a que os dias sejam todos definidos exactamente com a mesma duração. O ano foi cortado em pedaços de igual tamanho. O resultado é que se usarmos um relógio de sol para dizer a hora, este não dará necessariamente exactamente o mesmo tempo que o nosso relógio. Os relógios de sol exactos têm frequentemente uma tabela de correcções gravada que indica o número de minutos que o Sol está à frente ou atrás do GMT em diferentes alturas do ano. A diferença entre o tempo solar médio e o tempo solar real é chamada a equação do tempo. O Sol está mais atrasado em relação ao GMT por volta de 12 de Fevereiro, quando está cerca de 14 minutos e 20 segundos mais lento. Está mais à frente por volta de 3 de Novembro, quando está cerca de 16 minutos 23 segundos mais rápido. A posição do Sol coincide com o GMT em quatro dias do ano: 16 de Abril, 14 de Junho, 2 de Setembro e 25 de Dezembro, para que possa relaxar após a sua ceia de Natal, sabendo que o seu novo relógio de sol dirá a mesma hora que o seu relógio de sol.
Podemos traçar a posição do Sol às 12 horas GMT todos os dias do ano e isto dar-nos-á uma representação da equação do tempo no céu. Durante parte do ano, o Sol parecerá estar alguns minutos atrasado e estará ligeiramente a leste do devido sul. Noutras alturas do ano, o Sol estará ligeiramente à frente do GMT e aparecerá a oeste do verdadeiro sul. Plotar a posição ao longo do ano produzirá uma figura no céu que se parecerá com o numeral 8. O topo do 8 é a posição do Sol no solstício de Verão, quando este se encontra mais alto no céu. A parte inferior do 8 é a posição do Sol no solstício de Inverno, quando este atinge o seu ponto mais baixo no céu. Esta figura é chamada analemma.
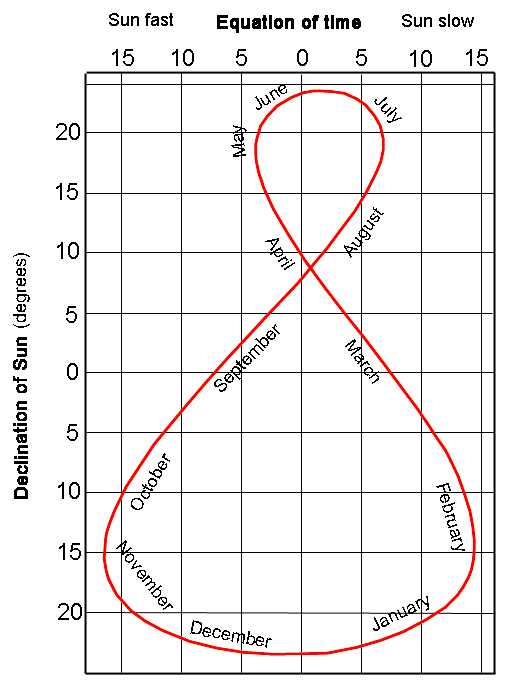
O analemma desenhado sobre um mapa do céu. O eixo horizontal mede o desfasamento em minutos, e o eixo vertical mede a declinação do Sol em graus.
Os quatro dias em que a posição do Sol coincide com o GMT podem ser lidos no gráfico, pois são os dias em que a figura do analemma cruza a linha zero vertical do gráfico.
O analemma tem a mesma forma em cada latitude, mas a sua posição no céu difere de lugar para lugar. Por exemplo, no Árctico, parte do laço sul nunca é visível, pois o Sol está completamente abaixo do horizonte em pleno Inverno; enquanto que no equador o analemma é traçado directamente por cima. E também, no hemisfério sul, o analemma aparece ao contrário em relação ao hemisfério norte.

O analemma marciano. Imagem © Dennis Mammana, usado por permissão.
Se a órbita da Terra fosse perfeitamente circular, então os dois lóbulos do analemma seriam imagens espelhadas um do outro. No entanto, como a órbita da Terra é elíptica, isto torna a forma do analemma assimétrica. A velocidade com que a Terra percorre a sua órbita depende da sua distância do Sol: quando está mais próxima do Sol, viaja mais depressa. Isto é descrito pela segunda lei de Kepler do movimento planetário, que afirma que uma linha que une a Terra e o Sol varre áreas iguais no mesmo tempo. A Terra atinge o seu ponto mais próximo do Sol por volta do dia 3 de Janeiro. Assim, em pleno Inverno do hemisfério norte, a Terra cobre todos os dias uma maior proporção da sua órbita do que no Verão do hemisfério norte. Isto afecta o aparecimento do analemma. O lóbulo que é traçado no hemisfério norte no Inverno é maior do que o que é traçado no Verão.
Também, se a data de aproximação mais próxima do Sol coincidisse exactamente com o solstício de Inverno, 21 de Dezembro, que corresponde ao ponto mais baixo do analemma, então o lado esquerdo do analemma seria uma imagem espelho do lado direito. Isto porque a Terra estaria a mover-se à mesma velocidade em torno do Sol em qualquer dia em particular após o solstício de Inverno, como o fez no mesmo número de dias antes do solstício de Inverno.
A excentricidade da órbita do planeta Marte é muito maior do que a excentricidade da órbita da Terra. Por outras palavras, a elipse formada pela órbita de Marte é mais esborrachada do que a da Terra. Por esta razão, o analemma em Marte tem a forma de uma pêra. Perdeu completamente um dos seus lóbulos. Na imagem à esquerda, a posição do Sol é traçada a cada 30 dias marcianos.
Nos últimos anos, o artista sírio Issam Kourbaj inspirou-se no mundo da ciência e, em particular, na luz e na óptica. Issam é artista em residência e bye-fellow no Christ’s College, Cambridge e tem usado o analemma como motivo durante o ano do 800º aniversário da Universidade. Esta foi a fonte de inspiração para a sua escultura de analemma, uma representação gerada por computador que é mostrada aqui.

Analemma animação de Nicholas Mee e Issam Kourbaj.
Issam também concebeu um relógio de sol analemma que foi utilizado como peça de arte performativa que fazia parte da Light Matter, uma celebração dos 800 anos da ciência na Universidade de Cambridge.
Se prefere dizer o seu tempo ao Sol do que o seu relógio de sol, então porque não construir o seu próprio relógio de sol analemático?
br>
Sobre o autor

 p>Nicholas Mee
p>Nicholas Mee Nicholas Mee estudou física e matemática de partículas na Universidade de Cambridge. Foi o Wrangler Sénior e aí completou um doutoramento com o título “Supersymmetric Quantum Mechanics and Geometry”. Nick está actualmente a escrever um livro sobre física de partículas chamado “The Forces of Nature” (As Forças da Natureza). É o fundador da empresa de software educativo Virtual Image e é o director britânico do projecto europeu de ciência e arte SCIENAR. Este artigo e o trabalho de Nick com Issam Kourbaj foram levados a cabo como parte da SCIENAR. Detalhes sobre os seus outros projectos estão disponíveis no seu website.
Issam Kourbaj é Artista em Residência e Bye-Fellow no Christ’s College, Cambridge. Nascido na Síria, formou-se em Damasco, Leninegrado e Londres e vem de uma formação em belas artes, arquitectura e design de teatro. O seu trabalho tem sido exibido em três continentes e é realizado em várias colecções, incluindo The British Museum.
Nos últimos anos, Issam inspirou-se no mundo da ciência, particularmente na luz e na óptica: a sua recente instalação Light Within, Life Without used camera obscura para encorajar as pessoas a olhar de forma diferente para cenas familiares, e foi exibida no Jardim Botânico em Cambridge como parte das celebrações do 800º aniversário da Universidade de Cambridge e na exposição Kettle’s Yard Upside Down/Inside Out. Também concebeu um relógio de sol analemma como peça de arte performativa, como parte do Light Matter e publicou recentemente o Cambridge Palimpsest – um puzzle em camadas e um mapa que traça o desenvolvimento da cidade ao longo do tempo – e trabalhou num desenho de cenário para o Let Newton Be! que foi apresentado em Cambridge. Como artista sírio residente no Reino Unido, foi recentemente seleccionado para participar no Imagine Art After, um projecto e exposição que teve lugar na Tate Britain em 2012.