Autómatos Finitos Determinísticos
Um autómato finito determinístico (DFA) é descrito por um tuple de cinco elementos: (Q,Σ,δ,q0,F)(Q, \Sigma, \delta, q_0, F)(Q,Σ,δ,q0,F).
QQQ = um conjunto finito de estados
Σ\SigmaΣ = um finito, alfabeto de entrada não vazia
δ\deltaδ = uma série de funções de transição
q0q_0q0 = o estado inicial
FFF = o conjunto de estados aceitáveis
Deve haver exactamente uma função de transição para cada símbolo de entrada em Σ\SigmaΣ de cada estado.
DFAs podem ser representados por diagramas desta forma: 
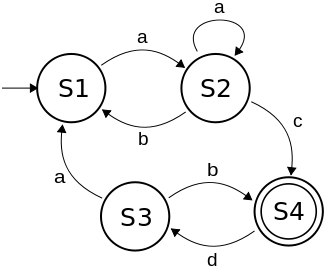
Que cadeia não pode ser gerada pela máquina de estados finitos abaixo?
Aqui está um diagrama DFA que descreve alguns movimentos simples que uma personagem num jogo de vídeo pode fazer: ficar de pé, correr, e saltar. Os botões que um jogador pode utilizar para controlar esta personagem em particular são “Para cima”, “A”, ou o jogador não pode premir nenhum botão.

Utilizando o diagrama de estados para o personagem do videojogo acima, descreva como um jogador pode controlar o seu personagem para ir de pé a correr para saltar.
Mostrar RespostaNo estado de pé, o jogador não pode premir nada e permanecer no estado de pé, depois, para passar ao estado de execução, o utilizador deve premir o botão “Para cima”. No estado de execução, o utilizador pode continuar a fazer correr o seu personagem premindo o botão “Para cima”, e depois, para passar ao estado de salto, o utilizador deve premir “A”.
Desenhar um diagrama para um DFA que reconheça a seguinte linguagem: A linguagem de todas as cordas que terminam com um 1.
Mostrar Resposta
Autómatos finitos não determinísticos
QQQQ = um conjunto finito de estados
Σ\SigmaΣ = um finito, alfabeto de entrada não vazio
δ\deltaδ = uma série de funções de transição
q0q_0q0 = o estado inicial
FFF = o conjunto de estados aceitáveis
DFAs não semelhantes, os NDFAs não são obrigados a ter funções de transição para cada símbolo em Σ\SigmaΣ, e podem existir múltiplas funções de transição no mesmo estado para o mesmo símbolo. Além disso, os NDFAs podem utilizar transições nulas, que são indicadas por ϵ\epsilonϵ. As transições nulas permitem que a máquina salte de um estado para outro sem ter de ler um símbolo.
Um NDFA aceita uma cadeia xxx se existir um caminho compatível com essa cadeia que termine num estado de aceitação.
NDFAs podem ser representados por diagramas desta forma:
 fonte
fonte
Descreva a linguagem que o NDFA acima reconhece.
Show AnswerO NDFA acima reconhece cordas que terminam em “10” e cordas que terminam em “01”.
State aaa é o estado inicial, e a partir daí, podemos criar uma cadeia com tantos 1’s e 0’s em qualquer ordem, e depois transferir para o estado bbb ou estado eee, ou podemos transferir imediatamente para o estado bbb ou estado eee. Em qualquer caso, o NDFA só aceitará uma corda que atinja o estado ddd ou state ggg. Para atingir o estado ddd ou state ggg, a cadeia deve terminar com um “01” (para o estado ddd) ou um “10” (para o estado ggg).
Por exemplo, as seguintes cadeias de caracteres são todas reconhecidas por este NDFA.
- 00000000010
- 10
- 01
- 1111101
Que corda não pode ser gerada pela máquina de estado finito abaixo?

Desenhar um diagrama para o NDFA que descreve a seguinte linguagem: A linguagem de todas as cordas que terminam com 1.
Mostrar resposta

