A eficiência de um algoritmo depende da quantidade de tempo, armazenamento e outros recursos necessários para executar o algoritmo. A eficiência é medida com a ajuda de notações assimptóticas.
Um algoritmo pode não ter o mesmo desempenho para diferentes tipos de entradas. Com o aumento do tamanho do input, o desempenho será alterado.
O estudo da alteração do desempenho do algoritmo com a alteração da ordem do tamanho do input é definido como análise assimptótica.
Notações assintóticas
Notações assintóticas são as notações matemáticas utilizadas para descrever o tempo de execução de um algoritmo quando o input tende para um determinado valor ou um valor limite.
Por exemplo: Na ordenação de bolhas, quando a matriz de entrada já está ordenada, o tempo gasto pelo algoritmo é linear, ou seja, o melhor caso.
Mas, quando a matriz de entrada está em estado inverso, o algoritmo leva o tempo máximo (quadrático) para ordenar os elementos, ou seja, o pior caso.
Quando a matriz de entrada não está ordenada nem em ordem inversa, então leva o tempo médio. Estas durações são indicadas usando notações assimptóticas.
Existem principalmente três notações assimptóticas:
- Notação de Big-O
- Notação de Omega
- Notação de Theta
Notação de Big-O (Notação O)
Notação de Big-O representa o limite superior do tempo de execução de um algoritmo. Assim, dá o pior caso de complexidade de um algoritmo.
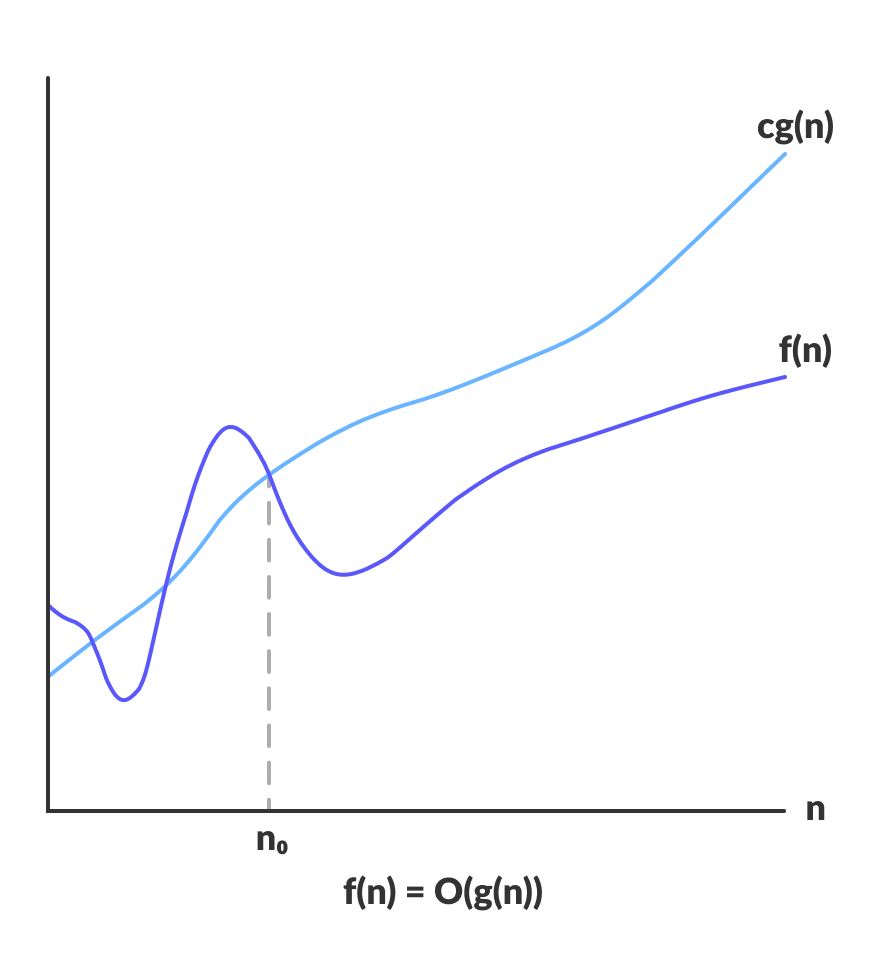
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
A expressão acima pode ser descrita como uma função f(n) pertence ao conjunto O(g(n)) se existir uma constante positiva c tal que se situe entre 0 e cg(n), para suficientemente grande n.
Para qualquer valor de n, o tempo de funcionamento de um algoritmo não ultrapassa o tempo fornecido por O(g(n)).
Desde que dá o pior caso de tempo de execução de um algoritmo, é amplamente utilizado para analisar um algoritmo, pois estamos sempre interessados no pior caso.
Omega Notation (Ω-notation)
Omega Notation representa o limite inferior do tempo de execução de um algoritmo. Assim, fornece a complexidade do melhor caso de um algoritmo.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
A expressão acima pode ser descrita como uma função f(n) pertence ao conjunto Ω(g(n)) se existir uma constante positiva c de tal forma que fique acima cg(n), para suficientemente grande n.
Para qualquer valor de n, o tempo mínimo requerido pelo algoritmo é dado por Omega Ω(g(n)).
Theta Notation (Θ-notation)
Theta notation encerra a função de cima e de baixo. Uma vez que representa os limites superior e inferior do tempo de execução de um algoritmo, é utilizada para analisar a complexidade média do caso de um algoritmo.
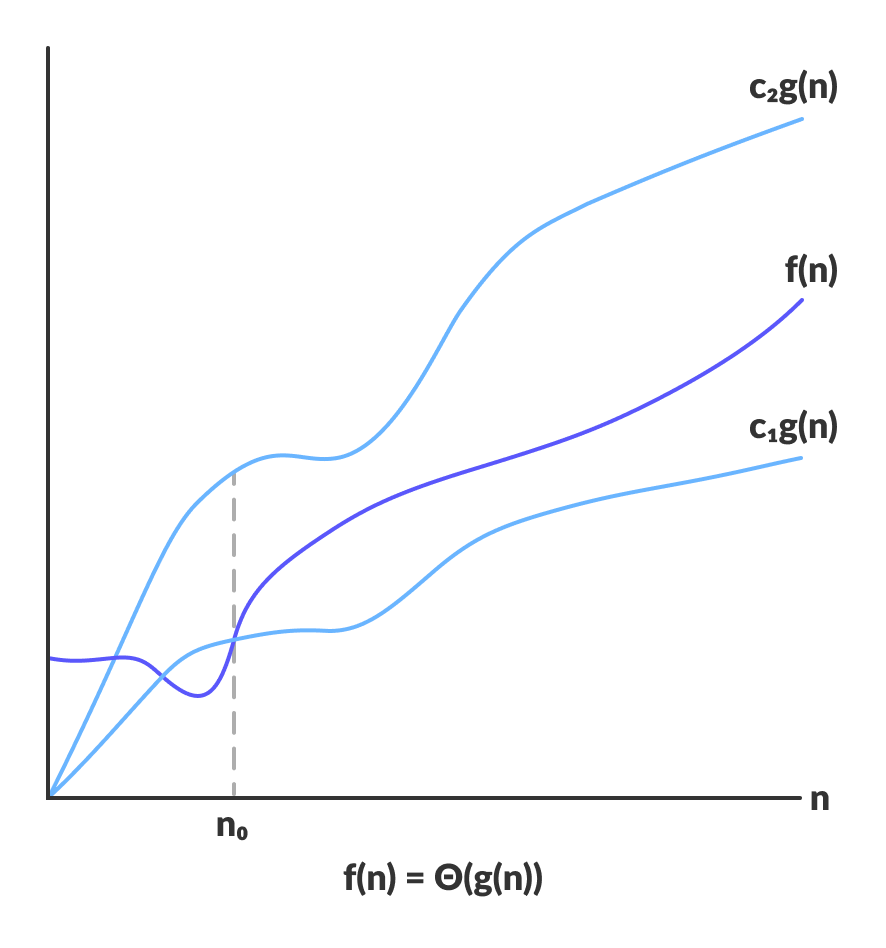
Para uma função g(n)Θ(g(n)) é dada pela relação:
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
A expressão acima pode ser descrita como uma função f(n) pertence ao conjunto Θ(g(n)) se existir constantes positivas c1 e c2 de modo a poder ser colada entre c1g(n) e c2g(n), para n.
se uma função f(n) se encontra em qualquer lugar entre c1g(n) e c2g(n) para todos n ≥ n0, então f(n) diz-se que é assimptóticamente apertado.