A força de Coriolis é um elemento central da dinâmica dos fluxos do oceano e da atmosfera. Uma derivação rigorosa utilizando cálculo vectorial é dada em muitos livros sobre mecânica clássica, mas tais derivações não são muitas vezes a forma mais eficaz de obter uma compreensão conceptual. Por conseguinte, forneceremos aqui uma explicação qualitativa mais intuitiva. Ao longo deste capítulo sobre fluxos geofísicos, temos falado muito sobre a 2ª lei de Newton, mas a chave para compreender a força de Coriolis é antes a 1ª lei de Newton: um objecto em movimento permanece em movimento com a mesma velocidade e na mesma direcção, a menos que actuado por uma força desequilibrada. A Terra e tudo o que nela está em constante movimento, à medida que a Terra gira em torno do seu eixo. Além disso, a direcção de todo este movimento muda constantemente: enquanto está a escrever na sua secretária às 14 horas, está a mover-se na direcção exactamente oposta à de quando estava deitado na sua cama às 2 horas da manhã. Estas mudanças forçadas na direcção do movimento dos objectos que tendem a continuar a mover-se na mesma direcção é o que dá origem às chamadas pseudo-forças (que na realidade são muito reais, se por acaso viver num planeta em rotação como a Terra).
A pseudo-força que é conceptualmente mais fácil de compreender é a força centrífuga, descrita abaixo.
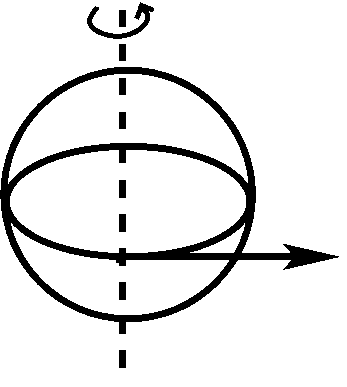
Essencialmente, os objectos tendem a ser atirados de um corpo em rotação, porque os objectos continuam a mover-se em linha recta (como indicado pela seta), enquanto a superfície do corpo em rotação não se move em linha recta (como indicado pelo círculo). Felizmente, não precisamos de nos preocupar em ser atirados para fora da Terra, porque a força gravitacional que mantém os nossos pés no chão é cerca de 300 vezes mais forte do que a força centrífuga. A força centrífuga não desempenha um papel significativo na dinâmica do oceano e da atmosfera, mas torna a Terra ligeiramente elíptica.
A força de Coriolis é uma pseudo-força que emerge quando um objecto se move na superfície de um corpo em rotação. A força de Coriolis é conceptualmente muito mais subtil do que a força centrífuga e, de facto, consiste em dois efeitos diferentes, cada um ilustrado abaixo:
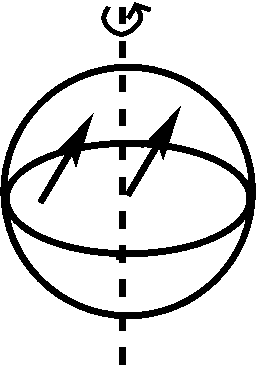
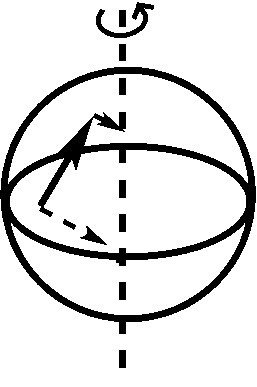
O painel esquerdo ilustra o primeiro efeito: um objecto que continua a mover-se na mesma direcção no espaço absoluto parece mudar de direcção, à medida que a Terra vira para a direita. No início, o objecto move-se directamente para Norte em direcção ao pólo (seta para a esquerda), mas depois, a direcção do movimento torna-se Nordeste no quadro de referência da Terra (seta para a direita), mesmo que a direcção e a velocidade do objecto não tenham mudado no espaço absoluto. O painel direito ilustra o segundo efeito: à medida que um objecto se move na superfície da Terra (como indicado pela seta sólida), transporta consigo a velocidade da rotação da Terra (setas tracejadas). medida que o objecto se move para Norte, entra em regiões onde a velocidade da rotação da Terra é menor do que na sua localização original. Assim, terá uma velocidade excessiva a Este que desvia o movimento do Norte para o Nordeste, quando visto no quadro de referência da Terra. Na moldura de referência da Terra, cada um destes 2 efeitos leva a uma aceleração com uma magnitude igual a (com a velocidade angular da Terra, a velocidade do objecto na moldura de referência da Terra), e a latitude), pelo que a aceleração total se soma ao parâmetro Coriolis (f = 2 vezes mega vmega vsin) ou fmega vsin), com o parâmetro Coriolis (f = 2 vezes mega vsin). A força de Coriolis está num ângulo de 90^^ (círculo) em relação ao movimento do objecto, à direita no hemisfério norte, à esquerda no hemisfério sul; desaparece no equador (theta=0)). Nas direcções zonal e meridional, as acelerações são de:
>p>
O impacto da força de Coriolis sobre as parcelas móveis de ar (ou água) é demonstrado aqui.
Contribuidores
- p>Dr. Anne Willem Omta (MIT)