Stosunek porównuje wartości.
Stosunek mówi ile jest jednej rzeczy w porównaniu do innej.

Istnieją 3 niebieskie kwadraty do 1 żółtego kwadratu
Stosunek może być pokazany na różne sposoby:
| Użyj „:” do oddzielenia wartości: | 3 : 1 | |
| Albo możemy użyć słowa „do”: | 3 do 1 | |
| Or write it like a fraction: | 31 |
Przełożenie można przeskalować:
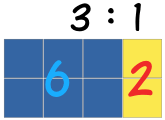
Tutaj stosunek wynosi również 3 niebieskie kwadraty do 1 żółtego kwadratu,
mimo że jest więcej kwadratów.
Używanie proporcji
Sztuczka z proporcjami polega na tym, aby zawsze mnożyć lub dzielić liczby przez tę samą wartość.
Przykład:
|
4 : 5 jest takie samo jak 4×2 : 5×2 = 8 : 10 |
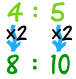 |
Przepisy
Przykład: Przepis na naleśniki wykorzystuje 3 szklanki mąki i 2 szklanki mleka.
Więc stosunek mąki do mleka wynosi 3 : 2
Aby zrobić naleśniki dla dużej ilości osób, możemy potrzebować 4 razy więcej, więc mnożymy liczby przez 4:
3×4 : 2×4 = 12 : 8
Innymi słowy, 12 szklanek mąki i 8 szklanek mleka.
Stosunek jest wciąż taki sam, więc naleśniki powinny być tak samo pyszne.
„Part-to-Part” and „Part-to-Whole” Ratios
Przykłady do tej pory były „part-to-part” (porównując jedną część do innej części).
Ale stosunek może również pokazać część w porównaniu do całej partii.
Przykład: Jest 5 szczeniaków, 2 to chłopcy, a 3 to dziewczynki

Part-to-Part:
Stosunek chłopców do dziewczynek wynosi 2:3 lub 2/3
Stosunek dziewczynek do chłopców wynosi 3:2 lub 3/2
Part-to-Whole:
Stosunek chłopców do wszystkich szczeniąt wynosi 2:5 lub 2/5
Stosunek dziewczynek do wszystkich szczeniąt wynosi 3:5 lub 3/5
Try It Yourself
Możemy używać proporcji do skalowania rysunków w górę lub w dół (przez mnożenie lub dzielenie).
|
Stosunek wysokości do szerokości flagi Indii wynosi 2:3 Więc na każde 2 (cale, metry, cokolwiek) wysokości |
 |
|
Jeśli zrobiliśmy flagę o wysokości 20 cali, powinna mieć 30 cali szerokości. Jeśli zrobiliśmy flagę o wysokości 40 cm, to jej szerokość powinna wynosić 60 cm (co nadal jest w stosunku 2:3) |
|
Przykład: Aby narysować konia w 1/10 normalnej wielkości, pomnóż wszystkie rozmiary przez 1/10
Ten koń w prawdziwym życiu ma 1500 mm wysokości i 2000 mm długości, więc stosunek jego wysokości do długości wynosi
1500 : 2000
Jaki jest ten stosunek, gdy narysujemy go w 1/10 normalnej wielkości?
| 1500 : 2000 | = 1500×1/10 : 2000×1/10 | |
| = 150 : 200 |
Możemy w ten sposób dokonać dowolnego zmniejszenia/powiększenia, jakie chcemy.
Duża stopa?
 |
Allie zmierzyła swoją stopę i miała ona 21cm długości, a następnie zmierzyła stopę swojej mamy i miała ona 24cm długości. |
„Muszę mieć duże stopy, moja stopa jest prawie tak długa jak mojej Mamy!”
Ale wtedy pomyślała, żeby zmierzyć wysokość i odkryła, że ma 133 cm wzrostu, a jej mama ma 152 cm.
W tabeli to jest:
| Allie | Mama | |
| Długość stopy: | 21cm | 24cm |
| Wysokość: | 133cm | 152cm |
Stosunek „stopy do wysokości” w stylu frakcji wynosi:
| Allie: | 21133 | Mama: | 24152 |
Więc stosunek dla Allie wynosi 21 : 133
To wciąż ten sam stosunek, prawda? Ponieważ podzieliliśmy obie liczby przez tę samą ilość.
A stosunek dla mamy wynosi 24 : 152
Tym razem podzieliliśmy przez 8, ale ten stosunek również pozostaje taki sam.
Uproszczone proporcje „stóp do wysokości” wynoszą teraz:
| Allie: | 319 | Mama: | 319 |
„Oh!”Więc moja stopa jest tylko tak duża, jak powinna być dla mojego wzrostu i nie jest zbyt duża”
.
