![]()
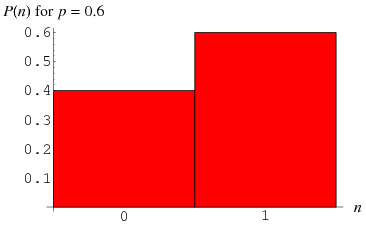
Rozkład Bernoulliego to rozkład dyskretny mający dwa możliwe wyniki oznaczone przez ![]() i
i ![]() , w którym
, w którym ![]() („sukces”) występuje z prawdopodobieństwem prawdopodobieństwem
(„sukces”) występuje z prawdopodobieństwem prawdopodobieństwem ![]() i
i ![]() („niepowodzenie”) zachodzi z prawdopodobieństwem
(„niepowodzenie”) zachodzi z prawdopodobieństwem ![]() , gdzie
, gdzie ![]() . Ma ona zatem funkcję gęstości prawdopodobieństwa
. Ma ona zatem funkcję gęstości prawdopodobieństwa
|
(1)
|
które można również zapisać
|
(2)
|
Odpowiednia funkcja rozkładu odpowiadającą jej funkcją rozkładu jest
|
(3)
|
Rozkład Bernoulliego jest zaimplementowany w języku WolframLanguage jako BernoulliDistribution.
Wykonanie stałej liczby prób ze stałym prawdopodobieństwem sukcesu w każdej próbie jest znane jako próba Bernoulliego.
Rozkład głów i reszek w rzucie monetą jest przykładem rozkładu Bernoulliego z ![]() . Rozkład Bernoulliego jest najprostszym rozkładem dyskretnym i stanowi podstawę dla innych, bardziej skomplikowanych rozkładów dyskretnych. Rozkłady wielu typów wariancji zdefiniowanych na podstawie ciągów niezależnych prób Bernoulliego, które są w jakiś sposób ograniczone, są podsumowane w poniższej tabeli (Evans et al. 2000, s. 32).
. Rozkład Bernoulliego jest najprostszym rozkładem dyskretnym i stanowi podstawę dla innych, bardziej skomplikowanych rozkładów dyskretnych. Rozkłady wielu typów wariancji zdefiniowanych na podstawie ciągów niezależnych prób Bernoulliego, które są w jakiś sposób ograniczone, są podsumowane w poniższej tabeli (Evans et al. 2000, s. 32).
| dystrybucja | definicja |
| rozkład dwumianowy | liczba sukcesów w |
| rozkład geometryczny | liczba niepowodzeń przed pierwszym sukcesem |
| rozkład dwumianowy ujemny | liczba niepowodzeń przed |
Funkcja charakterystyczna wynosi
|
(4)
|
i funkcja generująca momenta funkcją generującą moment jest
|
(5)
|
|||
|
(6)
|
|||
|
(7)
|
so
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
Te dają surowe momenty
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
i momenty centralne
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
Średnia, wariancja, skośność,i nadmiar kurtozy wynoszą
|
(18)
|
|||
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
Aby znaleźć estymator ![]() dla średniej populacji Bernoulliego ze średnią populacji
dla średniej populacji Bernoulliego ze średnią populacji ![]() , niech
, niech ![]() będzie liczebnością próby i załóżmy, że
będzie liczebnością próby i załóżmy, że ![]() sukcesów uzyskuje się z
sukcesów uzyskuje się z ![]() prób. Przyjmij estymator dany przez
prób. Przyjmij estymator dany przez
|
(22)
|
Więc prawdopodobieństwo uzyskania obserwowanego ![]() sukcesów w
sukcesów w ![]() próbach wynosi wówczas
próbach wynosi wówczas
|
(23)
|
Wartość oczekiwana estymatora ![]() jest zatem dana przez
jest zatem dana przez
|
(24)
|
|||
|
(25)
|
|||
|
(26)
|
Tak więc ![]() jest rzeczywiście bezstronnym estymatorem dla średniej populacji
jest rzeczywiście bezstronnym estymatorem dla średniej populacji ![]() .
.
Odchylenie średnie jest dane przez
|
(27)
|