Potrzeba rozróżnienia różnych znaczeń „ramki odniesienia” doprowadziła do powstania wielu różnych terminów. Na przykład, czasami rodzaj układu współrzędnych jest dołączany jako modyfikator, jak w kartezjańskim układzie odniesienia. Czasami podkreśla się stan ruchu, jak w obrotowym układzie odniesienia. Czasami podkreśla się sposób, w jaki przekształca się on w ramki uważane za pokrewne, jak w galileuszowym układzie odniesienia. Czasami ramy są rozróżniane ze względu na skalę obserwacji, jak w makroskopowych i mikroskopowych ramach odniesienia.
W niniejszym artykule termin obserwacyjny układ odniesienia jest używany wtedy, gdy nacisk kładzie się na stan ruchu, a nie na wybór współrzędnych, charakter obserwacji lub aparaturę obserwacyjną. W tym sensie obserwacyjny układ odniesienia umożliwia badanie wpływu ruchu na całą rodzinę układów współrzędnych, które mogą być dołączone do tego układu. Z drugiej strony, układ współrzędnych może być stosowany do wielu celów, w których stan ruchu nie jest głównym przedmiotem zainteresowania. Na przykład, układ współrzędnych może być przyjęty w celu wykorzystania symetrii systemu. W jeszcze szerszej perspektywie, przy formułowaniu wielu problemów w fizyce stosuje się uogólnione współrzędne, tryby normalne lub wektory własne, które są tylko pośrednio związane z przestrzenią i czasem. Wydaje się, że dla potrzeb poniższej dyskusji warto rozdzielić różne aspekty ram odniesienia. Przyjmujemy zatem obserwacyjne ramy odniesienia, układy współrzędnych i sprzęt obserwacyjny jako niezależne pojęcia, rozdzielone w następujący sposób:
- Rama obserwacyjna (taka jak inercjalna lub nieinercjalna rama odniesienia) jest pojęciem fizycznym związanym ze stanem ruchu.
- Układ współrzędnych jest pojęciem matematycznym, sprowadzającym się do wyboru języka używanego do opisu obserwacji. W konsekwencji, obserwator w obserwacyjnym układzie odniesienia może wybrać dowolny układ współrzędnych (kartezjański, biegunowy, krzywoliniowy, uogólniony, …) do opisu obserwacji dokonywanych z tego układu odniesienia. Zmiana w wyborze tego układu współrzędnych nie zmienia stanu ruchu obserwatora, a więc nie pociąga za sobą zmiany w obserwacyjnym układzie odniesienia obserwatora. Ten punkt widzenia można znaleźć również gdzie indziej. Co nie oznacza, że niektóre układy współrzędnych mogą być lepszym wyborem dla pewnych obserwacji niż inne.
- Wybór tego, co mierzyć i za pomocą jakiej aparatury obserwacyjnej jest sprawą odrębną od stanu ruchu obserwatora i wyboru układu współrzędnych.
Oto cytat mający zastosowanie do ruchomych ram obserwacyjnych R {{{displayplayfrak {{R}}}}

i różnych związanych z nimi trójprzestrzennych euklidesowych układów współrzędnych :
Wprowadzamy najpierw pojęcie ramki odniesienia, samo w sobie związane z ideą obserwatora: ramka odniesienia to w pewnym sensie „przestrzeń euklidesowa niesiona przez obserwatora”. Podajmy bardziej matematyczną definicję:… ramka odniesienia to… zbiór wszystkich punktów w przestrzeni euklidesowej o ruchu ciała sztywnego obserwatora. Ramka ta, oznaczana jako R {{displaystyle {{mathfrak {{R}}}}
, mówi się, że porusza się wraz z obserwatorem…. Położenia przestrzenne cząstek są oznaczane względem ramki R {{displaystyle {{mathfrak {R}}}
przez utworzenie układu współrzędnych R z początkiem O. Odpowiadający temu układowi zbiór osi, dzielący ruch ciała sztywnego ramy R {displaystyle {{mathfrak {R}}}
, można uznać za fizyczną realizację układu R {{displaystyle {{mathfrak {R}}}
. W ramce R {{displaystyle {{mathfrak {R}}}
, współrzędne są zmieniane z R na R′ poprzez przeprowadzenie, w każdej chwili czasu, tej samej transformacji współrzędnych na składowych obiektów nieodłącznych (wektorów i tensorów) wprowadzonych w celu reprezentacji wielkości fizycznych w tej ramie.
i to na temat użyteczności rozdzielenia pojęć R {{{displaystyle}}}

i :
Jak zauważył Brillouin, należy dokonać rozróżnienia między matematycznymi zbiorami współrzędnych a fizycznymi ramami odniesienia. Nieznajomość tego rozróżnienia jest źródłem wielu nieporozumień… funkcje zależne, takie jak na przykład prędkość, są mierzone w odniesieniu do fizycznego układu odniesienia, ale można swobodnie wybrać dowolny matematyczny układ współrzędnych, w którym określone są równania.
I to, również na temat rozróżnienia pomiędzy R {{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{{}}}}}}}}

i :
Pomysł ramki odniesienia jest naprawdę całkiem inny od pomysłu układu współrzędnych. Ramy różnią się tylko wtedy, gdy definiują różne przestrzenie (zbiory punktów spoczynku) lub czasy (zbiory jednoczesnych zdarzeń). Tak więc idee przestrzeni, czasu, spoczynku i jednoczesności są nierozerwalnie związane z ideą ramy. Jednak samo przesunięcie początku, czy czysto przestrzenny obrót współrzędnych przestrzennych skutkuje nowym układem współrzędnych. Tak więc ramy odpowiadają co najwyżej klasom układów współrzędnych.
i od J. D. Nortona:
W tradycyjnym rozwoju szczególnej i ogólnej teorii względności zwyczajowo nie rozróżnia się dwóch całkiem odrębnych idei. Pierwszą z nich jest pojęcie układu współrzędnych, rozumiane po prostu jako płynne, odwracalne przyporządkowanie czterech liczb do zdarzeń w czasoprzestrzeni. Drugie, układ odniesienia, odnosi się do wyidealizowanego systemu używanego do przypisywania takich liczb Aby uniknąć niepotrzebnych ograniczeń, możemy oddzielić ten układ od pojęć metrycznych. Dla naszych celów szczególnie ważne jest to, że każdy układ odniesienia ma określony stan ruchu w każdym zdarzeniu czasoprzestrzeni. W kontekście szczególnej względności i tak długo, jak ograniczamy się do ram odniesienia w ruchu inercjalnym, niewiele zależy od różnicy między inercjalnym układem odniesienia a inercjalnym układem współrzędnych, który on wywołuje. Ta komfortowa okoliczność natychmiast ustaje, gdy zaczynamy rozważać układy odniesienia w ruchu niejednostajnym, nawet w ramach szczególnej teorii względności…. Ostatnio, w celu wyeliminowania oczywistych niejednoznaczności w traktowaniu Einsteina, pojęcie układu odniesienia pojawiło się ponownie jako struktura różna od układu współrzędnych.
Dyskusja została podjęta przez Bradinga i Castellaniego poza prostymi czasoprzestrzennymi układami współrzędnych. Rozszerzenie na układy współrzędnych wykorzystujące uogólnione współrzędne leży u podstaw sformułowań Hamiltonianu i Lagrangianu kwantowej teorii pola, klasycznej mechaniki relatywistycznej i kwantowej grawitacji.
Układy współrzędnychEdit
Ale chociaż termin „układ współrzędnych” jest często używany (szczególnie przez fizyków) w sensie nietechnicznym, termin „układ współrzędnych” ma precyzyjne znaczenie w matematyce, a czasami to jest to, co fizyk ma na myśli, jak również.
Układ współrzędnych w matematyce jest aspektem geometrii lub algebry, w szczególności, właściwością rozmaitości (na przykład w fizyce, przestrzenie konfiguracyjne lub przestrzenie fazowe). Współrzędne punktu r w przestrzeni n-wymiarowej są po prostu uporządkowanym zbiorem n liczb:
r = . {{displaystyle {r} =.}

W ogólnej przestrzeni Banacha liczby te mogą być (na przykład) współczynnikami w rozszerzeniu funkcjonalnym, takim jak szereg Fouriera. W problemie fizycznym mogą to być współrzędne czasoprzestrzenne lub amplitudy trybu normalnego. W projekcie robota mogą to być kąty względnych obrotów, przemieszczenia liniowe lub deformacje stawów. Tutaj założymy, że współrzędne te mogą być odniesione do kartezjańskiego układu współrzędnych za pomocą zbioru funkcji:
x j = x j ( x , y , z , … ) , j = 1 , … , n , { {displaystyle x^{j}=x^{j}(x,y,z,^{j}(x,^{j}),^quad j=1,^{j},^ n,}

gdzie x, y, z, itd. są n współrzędnymi kartezjańskimi punktu. Biorąc pod uwagę te funkcje, powierzchnie współrzędnych definiuje się za pomocą zależności:
x j ( x , y , z , … ) = k o n s t a n t , j = 1 , … , n . {{displaystyle x^{j}(x,y,z,\) = {stała} ,\quad j=1,\i0,\i0,\i0,n.}

Przecinające się te powierzchnie definiują linie współrzędnych. W dowolnym wybranym punkcie, styczne do przecinających się w tym punkcie linii współrzędnych definiują zbiór wektorów bazowych {e1, e2, …, en} w tym punkcie. Czyli:
e i ( r ) = lim ϵ → 0 r ( x 1 , … , x i + ϵ , … , x n ) – r ( x 1 , … , x i , … , x n ) ϵ , i = 1 , … , n , {displaystyle \mathbf {e} _{i}(\mathbf {r} )=lim _{epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},\ x^{i}+ \epsilon ,\ x^{n} \prawica)- \mathbf {r} \left(x^{1},\ x^{i},\ x^{n}prawo)}{epsilon }},\quad i=1,\i0,\i0,\i0,n,}

które można znormalizować do jednostkowej długości. Więcej szczegółów można znaleźć we współrzędnych krzywoliniowych.
Powierzchnie współrzędnych, linie współrzędnych i wektory bazowe są elementami układu współrzędnych. Jeżeli wektory bazowe są ortogonalne w każdym punkcie, to układ współrzędnych jest ortogonalnym układem współrzędnych.
Ważnym aspektem układu współrzędnych jest jego tensor metryczny gik, który określa długość łuku ds w układzie współrzędnych w kategoriach jego współrzędnych:
( d s ) 2 = g i k d x i d x k , {{displaystyle (ds)^{2}=g_{ik} dx^{i} dx^{k},}

Gdzie powtarzające się indeksy są sumowane.
Jak wynika z tych uwag, układ współrzędnych jest konstrukcją matematyczną, częścią systemu aksjomatycznego. Nie ma koniecznego związku między układami współrzędnych a ruchem fizycznym (ani żadnym innym aspektem rzeczywistości). Układy współrzędnych mogą jednak zawierać czas jako współrzędną i mogą być używane do opisu ruchu. Tak więc, transformacje Lorentza i transformacje Galileusza mogą być postrzegane jako transformacje współrzędnych.
Ogólne i specyficzne tematy układów współrzędnych można realizować podążając za linkami Zobacz także poniżej.
Obserwacyjne ramy odniesieniaEdit

Obserwacyjny układ odniesienia, często nazywany fizycznym układem odniesienia, ramą odniesienia lub po prostu ramą, jest pojęciem fizycznym związanym z obserwatorem i stanem ruchu obserwatora. Przyjmujemy tutaj pogląd wyrażony przez Kumara i Barve: obserwacyjny układ odniesienia jest charakteryzowany jedynie przez jego stan ruchu. Jednak w tej kwestii nie ma jednomyślności. W szczególnej teorii względności rozróżnia się czasem między obserwatorem a ramką. Zgodnie z tym poglądem ramka to obserwator plus siatka współrzędnych skonstruowana jako ortonormalny prawoskrętny zbiór wektorów spacelike prostopadłych do wektora timelike. Zobacz Doran. Ten ograniczony pogląd nie jest tutaj używany i nie jest powszechnie przyjęty nawet w dyskusjach o względności. W ogólnej teorii względności użycie ogólnych układów współrzędnych jest powszechne (patrz, na przykład, rozwiązanie Schwarzschilda dla pola grawitacyjnego na zewnątrz izolowanej kuli).
Istnieją dwa rodzaje obserwacyjnych ram odniesienia: inercyjne i nieinercjalne. Inercyjny układ odniesienia definiuje się jako taki, w którym wszystkie prawa fizyki przyjmują swoją najprostszą postać. W szczególnej teorii względności ramy te są powiązane przez transformacje Lorentza, które są sparametryzowane przez prędkość. W mechanice newtonowskiej, bardziej ograniczona definicja wymaga jedynie, aby pierwsze prawo Newtona było prawdziwe; to znaczy, że inercyjny układ Newtona to taki, w którym swobodna cząstka porusza się po linii prostej ze stałą prędkością lub jest w spoczynku. Ramki te są powiązane przez transformacje Galileusza. Te relatywistyczne i newtonowskie transformacje są wyrażone w przestrzeniach o ogólnym wymiarze w postaci reprezentacji grupy Poincarégo i grupy Galileusza.
W przeciwieństwie do ramki inercyjnej, nieinercjalna ramka odniesienia to taka, w której do wyjaśnienia obserwacji należy powołać się na fikcyjne siły. Przykładem jest obserwacyjny układ odniesienia skupiony w punkcie na powierzchni Ziemi. Ten układ odniesienia orbituje wokół środka Ziemi, co wprowadza fikcyjne siły znane jako siła Coriolisa, siła odśrodkowa i siła grawitacji. (Wszystkie te siły, w tym grawitacja, znikają w prawdziwie inercyjnym układzie odniesienia, który jest układem swobodnego spadku.)
Aparatura pomiarowaEdit
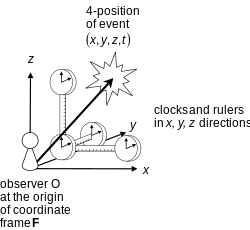
Kolejnym aspektem układu odniesienia jest rola aparatury pomiarowej (na przykład zegarów i prętów) dołączonej do tego układu (patrz cytat Nortona powyżej). Kwestia ta nie jest poruszana w tym artykule i jest szczególnie interesująca w mechanice kwantowej, gdzie relacja między obserwatorem a pomiarem jest wciąż przedmiotem dyskusji (patrz problem pomiaru).
W eksperymentach fizycznych rama odniesienia, w której laboratoryjne urządzenia pomiarowe są w spoczynku, jest zwykle nazywana ramą laboratoryjną lub po prostu „ramą laboratoryjną”. Przykładem może być rama, w której spoczywają detektory akceleratora cząstek. W niektórych eksperymentach rama laboratoryjna jest ramą inercyjną, ale nie jest to wymagane (na przykład laboratorium na powierzchni Ziemi w wielu eksperymentach fizycznych nie jest inercyjne). W eksperymentach fizyki cząstek często użyteczne jest przekształcanie energii i pędów cząstek z ramy laboratoryjnej, w której są one mierzone, do ramy środka pędu „ramy COM”, w której obliczenia są czasami uproszczone, ponieważ potencjalnie cała energia kinetyczna wciąż obecna w ramie COM może być użyta do tworzenia nowych cząstek.
W związku z tym można zauważyć, że zegary i pręty często używane do opisu urządzeń pomiarowych obserwatorów w myśli, w praktyce są zastąpione przez znacznie bardziej skomplikowaną i pośrednią metrologię, która jest związana z naturą próżni i wykorzystuje zegary atomowe, które działają zgodnie z modelem standardowym i które muszą być skorygowane o grawitacyjną dylatację czasu. (Patrz: sekunda, metr i kilogram).
W rzeczywistości Einstein uważał, że zegary i pręty są jedynie celowymi przyrządami pomiarowymi i powinny być zastąpione przez bardziej fundamentalne byty oparte na, na przykład, atomach i cząsteczkach.