Wprowadzenie
Na tej stronie omówione są naprężenia i odkształcenia główne. Chociaż nie omówiliśmy jeszcze wielu różnych definicji naprężeń i odkształceń, to w rzeczywistości prawdą jest, że wszystko, co tu omówiono, stosuje się niezależnie od rodzaju tensora naprężeń lub odkształceń. Na przykład, jeśli obliczymy wartości główne tensora naprężeń Cauchy’ego, to otrzymamy naprężenia główne Caucy’ego. Główne wartości tensora odkształceń Greena będą głównymi odkształceniami Greena.
Wszystko to wynika z dwóch faktów: Po pierwsze, wejściowe tensory naprężeń i odkształceń są symetryczne.Po drugie, omawiane tu przekształcenia współrzędnych mają zastosowanie do tensorów naprężeń i odkształceń (rzeczywiście mają).
Przedyskutujemy najpierw naprężenia, potem odkształcenia.
2-D Naprężenia główne

W 2-D, równania transformacji to
Są to rozwinięte formy \(\boldsymbol{\sigma}' = {\bf Q} \cdot \boldsymbol{\sigma} \cdot {\bf Q}^T\) w przestrzeni dwuwymiarowej.Można je również wyprowadzić z bilansu sił o przedstawionej tu postaci. Interesujące jest to, że naprężenie jest scharakteryzowane jako tensor, ponieważ jest zgodne z równaniem transformacji. Jest to jednak przede wszystkim argument matematyczny i nie miałby on większego znaczenia, gdyby nie był związany z fizyką równowagi sił. Fakt, że równanie transformacji współrzędnych prawidłowo odzwierciedla równowagę sił w różnych orientacjach, sprawia, że jest ono istotne.
Naprężenia główne są odpowiednimi naprężeniami normalnymi przy kącie, pod którym naprężenie ścinające jest równe zeru.
Ta strona wykonuje pełne trójwymiarowe transformacje tensorowe, ale może być nadal używana do problemów dwuwymiarowych. Wprowadź wartości w lewych górnych pozycjach 2×2 i obróć w płaszczyźnie 1-2, aby wykonać przekształcenia w 2-D. Poniższy zrzut ekranu przedstawia przypadek czystego ścinania obróconego o 45° w celu uzyskania naprężeń głównych. Zauważ również, jak przekształca się macierz.
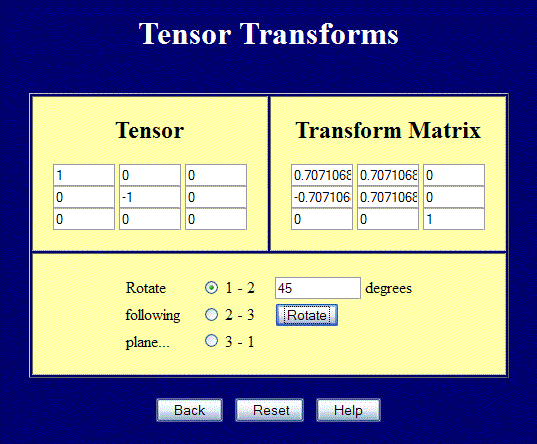
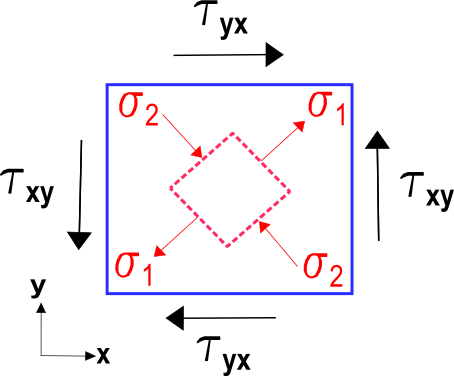
Na poniższym rysunku przedstawiono naprężenia odpowiadające przypadkowi czystego ścinania w przykładzie strony z transformacją tensorową. Niebieski kwadrat wyrównany z osiami wyraźnie ulega ścinaniu.Ale czerwony kwadrat wpisany w większy niebieski kwadrat widzi tylko proste rozciąganie i ściskanie.Są to główne wartości przypadku czystego ścinania w globalnym układzie współrzędnych.
W przestrzeni dwuwymiarowej, orientację naprężenia głównego, \(\tau’\), można obliczyć przez wstawienie \(\tau’\!_{xy} = 0\) do powyższego równania ścinania i rozwiązanie dla \(\tau’\), aby otrzymać \(\tau’\), czyli kąt naprężenia głównego. acierz transformacji, \(\ Q}, ma postać
Wstawiając tę wartość \(\theta_P\) z powrotem do równań naprężeń normalnych, otrzymujemy wartości główne. Zapisuje się je jako \(\sigma_{max}\) i \(\sigma_{min}\) lub alternatywnie jako \(\sigma_1\) i \(\sigma_2\).
Można je również uzyskać, stosując \(\boldsymbol{sigma}' = {\bf Q} \cdot \boldsymbol{\sigma} \cdot {\bf Q}^T\) z \(\bf Q}) na podstawie \(\theta_P\).
3-D Principal Stresses
Transformacje współrzędnych w przestrzeni trójwymiarowej to
= ∗ druga macierz ∗ jest ponownie transpozycją pierwszej.
Ta strona wykonuje transformacje tensorowe.
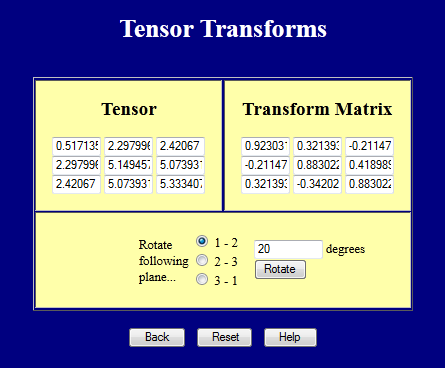
A ta strona oblicza wartości główne (wartości własne) i kierunki główne (wektory własne).
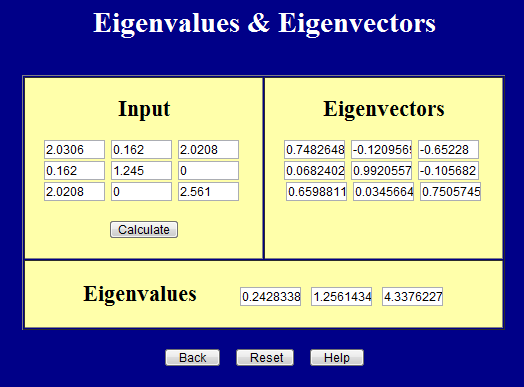
Ważne jest, aby pamiętać, że dane wejściowe do obu stron muszą być symetryczne. W rzeczywistości obie strony to wymuszają.
Wartości własne powyżej można zapisać w postaci macierzy jako
2-D Odkształcenia główne
Mechanika obliczania odkształceń głównych jest identyczna jak w przypadku obliczania naprężeń głównych. Jedyną potencjalną przeszkodą, o której należy pamiętać, jest to, że równania zawsze działają na połowie wartości ścinania, ∗(∗gamma / 2}).
W 2-D, równania transformacji są zapisane w kategoriach ∗(∗gamma / 2}), aby podkreślić, że połowa wszystkich wartości ścinania jest używana w równaniach transformacji.
Ta strona wykonuje pełne trójwymiarowe transformacje tensorowe, ale nadal może być używana do problemów dwuwymiarowych. Wprowadź wartości w lewych górnych pozycjach 2×2 i obróć w płaszczyźnie 1-2, aby wykonać transformacje w 2-D. Poniższy zrzut ekranu przedstawia przypadek czystego ścinania obróconego o 45° w celu uzyskania odkształceń głównych. Zauważ również, jak przekształca się macierz ∗.

Następny rysunek przedstawia zdeformowane kształty odpowiadające przypadkowi czystego ścinania w przykładzie strony internetowej z transformacją tensorową. Niebieski kwadrat wyrównany z osiami wyraźnie ulega ścinaniu.Ale czerwony kwadrat wpisany w większy niebieski kwadrat widzi tylko proste rozciąganie i ściskanie.Są to główne wartości czystego odkształcenia ścinającego w globalnym układzie współrzędnych.
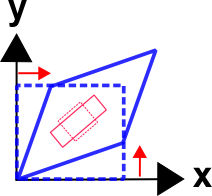
W przestrzeni dwuwymiarowej, orientację odkształcenia głównego, \(\theta_P\), można obliczyć przez ustawienie \(\gamma’\!_{xy} = 0\) w powyższym równaniu ścinania i rozwiązanie dla \(\theta_P\), aby otrzymać \(\theta_P\), główny kąt odkształcenia. acierz transformacji, \({{bf Q}}, ma postać
Wstawiając tę wartość \(\theta_P}) z powrotem do równań dla odkształceń normalnych, otrzymujemy wartości główne. Zapisuje się je jako \(\epsilon_{max}\) i \(\epsilon_{min}\) lub alternatywnie jako \(\epsilon_1\) i \(\epsilon_2\).
Można je również uzyskać za pomocą \(\bf E}' = \bf Q} \cdot {\bf E} \cdot {\bf Q}^T\) z \(\bf Q}) na podstawie \(\theta_P\).
Trójwymiarowe naprężenia główne
Transformacje współrzędnych w trójwymiarze to
= ∗ druga macierz ∗ jest ponownie transpozycją pierwszej.
Ta strona wykonuje transformacje tensorowe.

A ta strona oblicza wartości główne (wartości własne) i kierunki główne (wektory własne).

Należy pamiętać, że dane wejściowe do obu stron muszą być symetryczne. W rzeczywistości obie strony to wymuszają.
Wartości własne powyżej można zapisać w postaci macierzowej jako
Podsumowanie
Ta zasada niezmienniczości wielkości przy przekształceniach współrzędnych jest w rzeczywistości uniwersalna dla wszystkich macierzy, które są symetryczne i przekształcane zgodnie z zasadą
gdzie \u2002
jest „dowolną macierzą symetryczną”.
Przypomnijmy, że iloczyn każdej macierzy z jej transpozycją jest zawsze wynikiem symetrycznym, więc ten wynik będzie się kwalifikował. Jest to szczególnie istotne dla \(\bf F}^T \bf F}), którego niezmienniki są używane w prawie Mooneya-Rivlina dotyczącym zachowania gumy. Prawo Mooneya-Rivlina i jego współczynniki zostaną omówione na tej stronie. Jako dodatkową zapowiedź zobaczymy, że trzeci niezmiennik \(\bf F}^T \bf F} dla gumy zawsze równa się 1, ponieważ guma jest nieściśliwa. Jest to więc nie tylko stała, niezależna od przekształceń współrzędnych, ale nawet stała wartość, zawsze równa 1, niezależna od przekształceń współrzędnych i stanu odkształcenia.