Efektywność algorytmu zależy od ilości czasu, pamięci i innych zasobów potrzebnych do wykonania algorytmu. Wydajność jest mierzona za pomocą notacji asymptotycznych.
Algorytm może nie mieć takiej samej wydajności dla różnych typów danych wejściowych. Wraz ze wzrostem rozmiaru danych wejściowych wydajność będzie się zmieniać.
Badanie zmiany wydajności algorytmu wraz ze zmianą rzędu wielkości danych wejściowych jest określane jako analiza asymptotyczna.
Notacje asymptotyczne
Notacje asymptotyczne to notacje matematyczne używane do opisania czasu działania algorytmu, gdy dane wejściowe mają tendencję do osiągania określonej wartości lub wartości granicznej.
Na przykład: W sortowaniu bąbelkowym, gdy tablica wejściowa jest już posortowana, czas pobierany przez algorytm jest liniowy tj. najlepszy przypadek.
Ale gdy tablica wejściowa jest w stanie odwróconym, algorytm pobiera maksymalny czas (kwadratowy) na posortowanie elementów tj. najgorszy przypadek.
Gdy tablica wejściowa nie jest ani posortowana, ani w stanie odwróconym, wtedy pobiera średni czas. Te czasy są oznaczane przy użyciu notacji asymptotycznych.
Istnieją głównie trzy notacje asymptotyczne:
- Notacja Big-O
- Notacja Omega
- Notacja Theta
Notacja Big-O (O-notacja)
Notacja Big-O reprezentuje górną granicę czasu działania algorytmu. Daje więc złożoność algorytmu w najgorszym przypadku.
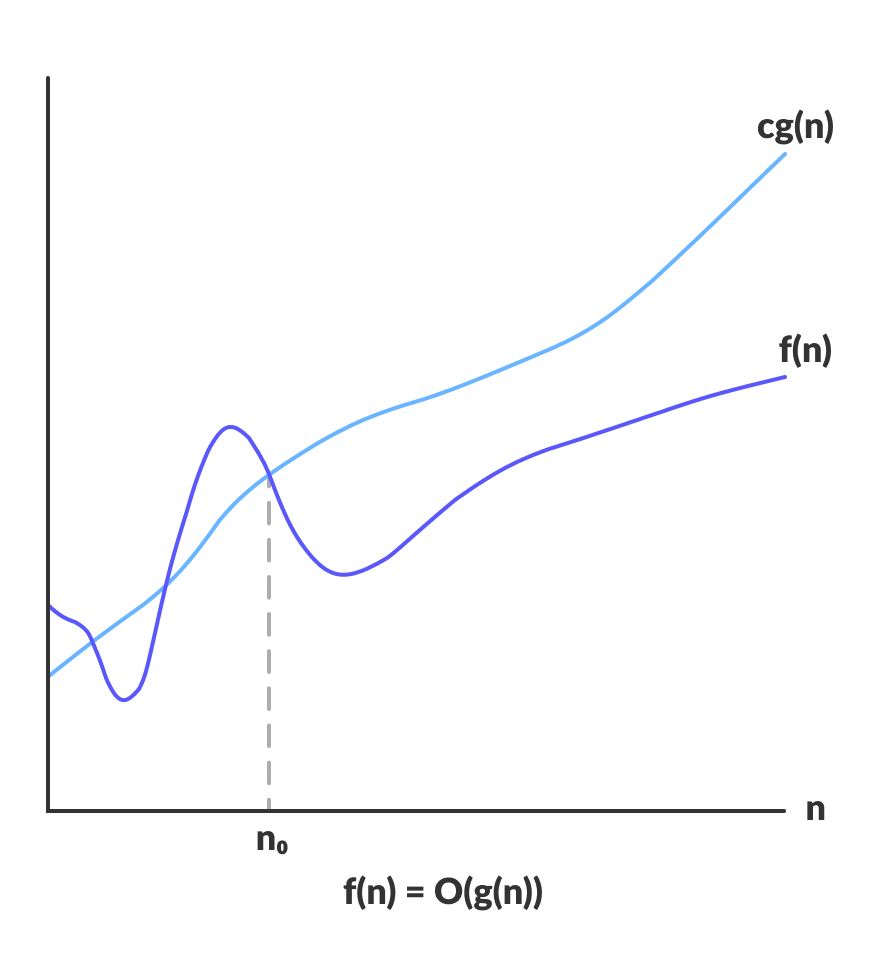
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
Powyższe wyrażenie można opisać jako funkcję f(n) należy do zbioru O(g(n)) jeśli istnieje stała dodatnia c taka, że leży pomiędzy 0 a cg(n), dla wystarczająco dużych n.
Dla dowolnej wartości n, czas działania algorytmu nie przekracza czasu podanego przez O(g(n)).
Ponieważ daje najgorszy czas działania algorytmu, jest szeroko stosowany do analizy algorytmu, ponieważ zawsze jesteśmy zainteresowani najgorszym scenariuszem.
Omega Notacja (Ω-notacja)
Omega notacja reprezentuje dolną granicę czasu działania algorytmu. Zapewnia więc złożoność algorytmu w najlepszym przypadku.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
Powyższe wyrażenie można opisać jako funkcję f(n) należy do zbioru Ω(g(n)) jeśli istnieje dodatnia stała c taka, że leży powyżej cg(n), dla wystarczająco dużych n.
Dla dowolnej wartości n, minimalny czas wymagany przez algorytm jest dany przez Omegę Ω(g(n)).
Notacja Theta (Θ-notacja)
Notacja Theta obejmuje funkcję z góry i z dołu. Ponieważ reprezentuje ona górną i dolną granicę czasu działania algorytmu, jest używana do analizy średniej złożoności algorytmu.
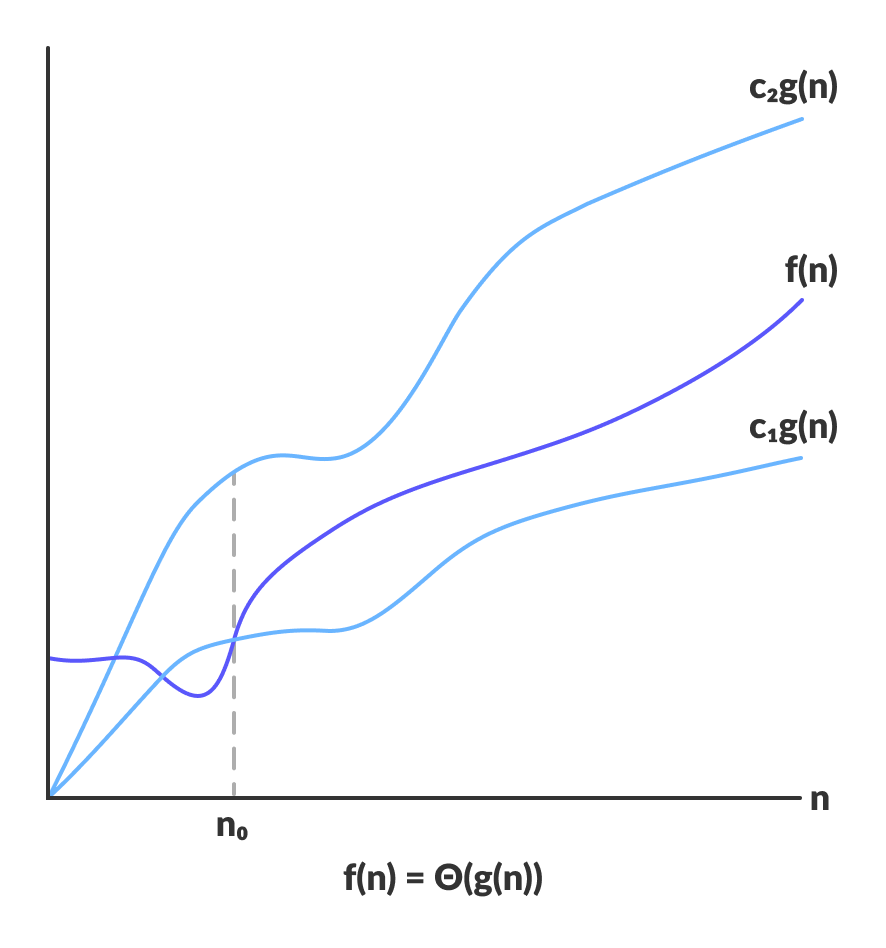
Dla funkcji g(n)Θ(g(n)) dana jest zależność:
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
Powyższe wyrażenie można opisać w ten sposób, że funkcja f(n) należy do zbioru Θ(g(n)) jeśli istnieją m.in. dodatnie stałe c1 i c2 takie, że można ją umieścić pomiędzy c1g(n) i c2g(n), dla wystarczająco dużego n.
Jeśli funkcja f(n) leży w dowolnym miejscu pomiędzy c1g(n) i c2g(n) dla wszystkich n ≥ n0, to f(n) mówi się, że jest asymptotycznie ściśle związany.