
Będę szczery. Zajmowałem się poważnymi sprawami związanymi z rachunkiem przez więcej lat niż chciałbym przyznać. Czasami w fizyce, musisz po prostu integrować rzeczy. To się zdarza.
Jednakże, kiedy pomagałem mojemu synowi na zajęciach z rachunków, zacząłem zdawać sobie sprawę – co do cholery dzieje się z całkowaniem? Czuję, że mam naprawdę solidne zrozumienie pochodnych – ale całkowanie ma jakieś dziwne rzeczy.
Cóż, nigdy nie zrozumiesz rzeczy, dopóki nie rozbijesz ich na podstawowe kawałki. Więc, to jest to, co zamierzam zrobić. Znajdę pole powierzchni pod krzywą na trzy różne sposoby.
Area using summation notation
To jest najłatwiejsze do zrozumienia, ale najtrudniejsze do obliczenia. Oh wait! Dlaczego znajdujemy pole powierzchni pod krzywą? OK, poczekaj – mój przykład na końcu powinien pomóc.
Podstawową ideą jest podzielenie obszaru na N prostokątów (gdzie N jest po prostu jakąś liczbą). Następnie mogę znaleźć obszar każdego prostokąta i dodać je, aby uzyskać całkowity obszar. Im więcej kawałków, na które go podzielę, tym lepsza odpowiedź – więc napiszę wyrażenie dla tego obszaru i wezmę limit, gdy liczba kawałków idzie do nieskończoności.

Powierzchnię oblicza się wówczas jako:
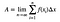
Po tym jest dużo rzeczy – i robi się to trochę nużące. Jednak MUSISZ przez to przejść, aby w pełni zrozumieć całą sprawę. Oto filmik, w którym przeprowadzam Cię przez to.
Jeśli używasz funkcji:
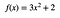
Obszar od x = 1 do x =2 wynosi 9 (niezależnie od tego, jakie powinny być jednostki – nie jestem matematykiem, więc przeszkadza mi pominięcie jednostek).
Area using anti-derivatives
Istnieje pewna sztuczka. To jest niesamowita sztuczka. Możesz napisać obszar pod krzywą jako całkę definitywną (gdzie całka jest nieskończoną sumą nieskończenie małych kawałków – tak jak notacja sumowania).
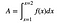
Teraz dla szalonych rzeczy. CRAZY. Okazuje się, że obszar jest antypochodną f(x). Jeśli zatrzymasz się na chwilę, zobaczysz, że to jest dzikie. Szalenie dzikie. Jeśli pochodna mówi ci coś o nachyleniu krzywej, to przeciwieństwo pochodnej mówi ci o polu powierzchni pod krzywą?
Tak. Jest to podstawowe twierdzenie rachunku. Oto moje wyjaśnienie (tak, w tym poście będzie kilka filmów i jesteś ZOBOWIĄZANY do obejrzenia ich wszystkich.
Właściwie, jest jeszcze jedna ważna rzecz. Całka definitywna od x = 1 do x =2 jest różnicą funkcji powierzchni A(2) i A(1). Nie będę się zagłębiał w szczegóły, ponieważ mój umysł nadal jest zdmuchnięty przez tę anty-pochodną rzecz.
Ale tutaj jest obszar pod tą SAMĄ funkcją, ale z całkowaniem.
Tak. Otrzymujesz ten sam wynik końcowy. Powierzchnia = 9 kurczaków² (dodałem jednostki powierzchni).
Powierzchnia przy użyciu obliczeń numerycznych
Teraz przechodzimy do zabawnych rzeczy. Co by się stało, gdybym znalazł pole powierzchni pod krzywą poprzez zsumowanie pól powierzchni kilku prostokątów? Oh wait… już to zrobiłem w pierwszej metodzie. Ale co powiesz na to – nie robię nieskończonej liczby prostokątów, tylko dużą liczbę prostokątów? To jest dokładnie to, o co chodzi w obliczeniach numerycznych.
Oczywiście, jeśli podzielę obszar na 100 kawałków, będę musiał wykonać 100 zestawów obliczeń obszaru. Czy ktoś naprawdę chce to robić? Nie – nikt nie uważa, że byłoby to zabawne. Ale wiesz, kogo to nie obchodzi? Komputery (komputery elektroniczne).
Tak, możemy dostać komputer, aby wykonać tę serię obliczeń. Musimy tylko dać mu kilka instrukcji, a wtedy on pójdzie i wykona swoją pracę. To będzie wspaniałe. Oto podstawowy przepis, którego będzie używał.
- Zdecyduj, na ile kawałków chcesz rozbić krzywą. Co powiesz na 100? Mając to oraz początkową i końcową wartość x, możesz obliczyć szerokość każdego prostokąta (Δx).
- Ustaw obszar na zero (kurcze²). Będziemy ciągle dodawać do tej wartości, ale musi się ona gdzieś zaczynać.
- Zacznij od początkowej wartości x (w przykładzie, którego używałem – to x = 1).
- Oblicz wysokość prostokąta. Będzie to f(x) przy bieżącej wartości x.
- Znajdź obszar tego prostokąta i dodaj go do całkowitego obszaru.
- Przejdź na następną wartość x i powtarzaj, aż dojdziesz do końcowej wartości x.
To jest tak proste, że nawet komputer mógłby to zrobić. OK, ja się tylko bawię. Niektórzy z moich najlepszych przyjaciół to komputery.
Tutaj jest kod do tego obliczenia w pythonie (tutaj jest link do rzeczywistego kodu).
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
Z N = 100, otrzymuję obszar 8,95505 – który NIE jest dokładnie 9 kurczaków², ale jest całkiem darn blisko. Wystarczająco blisko dla większości obliczeń kwadratowych kurczaków.
Tylko kilka szybkich komentarzy na temat tego kodu.
- Pomyślałem, że byłoby zabawnie uczynić funkcję rzeczywistą funkcją pythona (to jest część
def f(t):. - Pierw obliczam obszar małego prostokąta (dA), a następnie dodaję go do całkowitego obszaru.
- Ta metoda faktycznie ma prostokąty wyłożone funkcją po lewej stronie górnej części prostokąta. Można to zrobić z prawej strony zbyt.
- Zrobiłem również wideo dla tego. Ale nie musisz go oglądać – w większości wyjaśniłem to już tutaj.
Co jeśli nie masz funkcji matematycznej?
Pozwól, że postawię cię w następującej sytuacji. Jesteś w samochodzie, który jedzie i możesz TYLKO zobaczyć prędkościomierz. Zapisujesz wartość prędkości co sekundę (ponieważ jesteś super szybkim notatnikiem). Samochód w końcu się zatrzymuje, a ty musisz się dowiedzieć, jak daleko zaszedłeś.
Oto coś takiego (używając wózka Verniera z czujnikiem ruchu – ale masz pojęcie, że to jest to samo, co prawdziwy samochód).

OK – ostrzeżenie, Będę tu oszukiwał. Tor noniuszowy zbiera dane o położeniu na podstawie tych linii na torze. Na podstawie danych o położeniu, oblicza prędkość. Tak więc, mam już pozycję wózka – ale udawajmy, że podaje on tylko prędkość w funkcji czasu. Może wyglądałoby to mniej więcej tak.

Zobacz. To nie jest funkcja – to jest stacja kosmiczna. Nie, zaraz – to z Gwiezdnych Wojen. Ale i tak nie jest to funkcja matematyczna. To tylko dane. Nie można znaleźć antypochodnej danych (no, nie używając normalnych reguł i innych rzeczy). Ale czekaj! Integracja numeryczna działa tak samo dobrze.
Oczywiście, jest tu coś jeszcze ważnego. Jest to pomysł, że are pod tą krzywą reprezentuje coś rzeczywistego. Wyobraźmy sobie, że mamy samochód poruszający się ze stałą prędkością przez pewien czas. Mógłbyś dość łatwo obliczyć jego przemieszczenie:
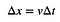
Jeśli masz wykres prędkości vs. czasu, ta stała prędkość wyglądałaby jak prostokąt. Tak, powierzchnia tego prostokąta byłaby równa v*Δt. Jeśli NIE jest to stała prędkość, obszar pod wykresem prędkość-czas nadal byłby przemieszczeniem.
OK, ostatni filmik. Tutaj jest moje wyjaśnienie kodowania, aby rozwiązać ten problem z przemieszczeniem.
Zapewnij się, że obejrzysz wszystkie filmy.