Een verhouding vergelijkt waarden.
Een verhouding zegt hoeveel er van één ding is in vergelijking met een ander ding.

Er zijn 3 blauwe vierkantjes tegen 1 geel vierkantje
Ratio’s kunnen op verschillende manieren worden weergegeven:
| Gebruik de “:” om de waarden te scheiden: | 3 : 1 | |
| 3 tot 1 | ||
| Of we schrijven het als een breuk: | 31 |
Een verhouding kan worden opgeschaald:
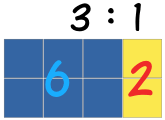
Hier is de verhouding ook 3 blauwe vierkantjes op 1 geel vierkantje,
ook al zijn er meer vierkantjes.
Verhoudingen gebruiken
De truc met verhoudingen is om de getallen altijd met dezelfde waarde te vermenigvuldigen of te delen.
Voorbeeld:
|
4 : 5 is hetzelfde als 4×2 : 5×2 = 8 : 10 |
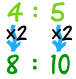 |
Recepten
Voorbeeld: Een recept voor pannenkoeken gebruikt 3 kopjes bloem en 2 kopjes melk.
Dus de verhouding bloem : melk is 3 : 2
Om pannenkoeken te maken voor heel veel mensen hebben we misschien 4 keer de hoeveelheid nodig, dus vermenigvuldigen we de getallen met 4:
3×4 : 2×4 = 12 : 8
Met andere woorden, 12 kopjes bloem en 8 kopjes melk.
De verhouding is nog steeds hetzelfde, dus de pannenkoeken zouden net zo lekker moeten zijn.
“Deel-op-deel” en “Deel-op-geheel” Verhoudingen
De voorbeelden tot nu toe waren “deel-op-deel” (het ene deel vergelijken met het andere deel).
Maar een verhouding kan ook een deel laten zien ten opzichte van de hele partij.
Voorbeeld: Er zijn 5 pups, 2 zijn jongens, en 3 zijn meisjes

Deel-tegen-deel:
De verhouding jongens-meisjes is 2:3 of 2/3
De verhouding meisjes-jongens is 3:2 of 3/2
Deel-tegen-geheel:
De verhouding tussen jongens en alle pups is 2:5 of 2/5
De verhouding tussen meisjes en alle pups is 3:5 of 3/5
Probeer het zelf
We kunnen verhoudingen gebruiken om tekeningen naar boven of beneden te schalen (door te vermenigvuldigen of te delen).
|
De hoogte-breedteverhouding van de Indiase vlag is 2:3 Dus voor elke 2 (inches, meters, wat dan ook) hoogte |
 |
|
Als we de vlag 20 inch hoog maken, moet hij 30 inch breed zijn. Als we de vlag 40 cm hoog hebben gemaakt, moet hij 60 cm breed zijn (wat nog steeds in de verhouding 2:3 is) |
|
Voorbeeld: Om een paard op 1/10e normale grootte te tekenen, vermenigvuldigt u alle maten met 1/10e
Dit paard is in het echt 1500 mm hoog en 2000 mm lang, dus de verhouding tussen zijn hoogte en lengte is
1500 : 2000
Wat is die verhouding als we het op 1/10e normale grootte tekenen?
| 1500 : 2000 | = 1500×1/10 : 2000×1/10 | ||
| = 150 : 200 |
Op die manier kunnen we elke verkleining/vergroting maken die we maar willen.
Grote voet?
 |
Allie heeft haar voet opgemeten en die was 21 cm lang, en toen heeft ze de voet van haar moeder opgemeten, en die was 24 cm lang. |
“Ik heb vast grote voeten, mijn voet is bijna net zo lang als die van mijn moeder!”
Maar toen dacht ze eraan de hoogte te meten, en ontdekte dat zij 133 cm lang is, en haar moeder 152 cm.
In een tabel is dit:
| Allie | Mam | |
| 21cm | 24cm | |
| Hoogte: | 133cm | 152cm |
De “voet-hoogte” verhouding in breukstijl is:
| Allie: | 21133 | Mama: | 24152 |
Dus de verhouding voor Allie is 21 : 133
Het is nog steeds dezelfde verhouding, toch? Want we hebben beide getallen evenveel gedeeld.
En de verhouding voor mama is 24 : 152
Dit keer hebben we door 8 gedeeld, maar ook die verhouding blijft hetzelfde.
De vereenvoudigde “voet-hoogte” verhoudingen zijn nu:
| Allie: | 319 | Mam: | 319 |
“Oh!” zei ze, “de verhoudingen zijn hetzelfde”.
“Dus mijn voet is maar zo groot als hij zou moeten zijn voor mijn lengte, en is niet echt te groot.”
