Referentiekader

De noodzaak om onderscheid te maken tussen de verschillende betekenissen van “referentiekader” heeft geleid tot een verscheidenheid aan termen. Soms wordt bijvoorbeeld het type coördinatenstelsel als modifier toegevoegd, zoals in Cartesian frame of reference. Soms wordt de bewegingstoestand benadrukt, zoals in het roterende referentiekader. Soms wordt de wijze van transformatie naar als verwant beschouwde kaders benadrukt, zoals in het Galileïsch referentiekader. Soms worden kaders onderscheiden door de schaal van hun waarnemingen, zoals in macroscopische en microscopische referentiekaders.

In dit artikel wordt de term waarnemingskader gebruikt wanneer de nadruk ligt op de bewegingstoestand en niet zozeer op de keuze van de coördinaten of de aard van de waarnemingen of de waarnemingsapparatuur. In die zin maakt een waarnemingskader het mogelijk het effect van beweging te bestuderen op een hele familie van coördinatenstelsels die aan dit kader kunnen worden gekoppeld. Anderzijds kan een coördinatenstelsel worden gebruikt voor vele doeleinden waarbij de toestand van de beweging niet de eerste zorg is. Zo kan een coördinatenstelsel bijvoorbeeld worden gebruikt om voordeel te halen uit de symmetrie van een systeem. In een nog ruimer perspectief wordt bij de formulering van vele problemen in de fysica gebruik gemaakt van veralgemeende coördinaten, normale modi of eigenvectoren, die slechts indirect verband houden met ruimte en tijd. Het lijkt nuttig de verschillende aspecten van een referentiekader te scheiden voor de bespreking hieronder. We nemen daarom waarnemingskaders, coördinatenstelsels en waarnemingsapparatuur als onafhankelijke begrippen, gescheiden als volgt:

• Een waarnemingskader (zoals een inertiaal of niet-inertiaal referentiekader) is een natuurkundig begrip dat betrekking heeft op de toestand van beweging.
• Een coördinatenstelsel is een wiskundig begrip, dat neerkomt op een taalkeuze die wordt gebruikt om waarnemingen te beschrijven. Bijgevolg kan een waarnemer in een referentiekader ervoor kiezen om om het even welk coördinatenstelsel (cartesiaans, polair, kromlijnig, gegeneraliseerd, …) te gebruiken om waarnemingen vanuit dat referentiekader te beschrijven. Een verandering in de keuze van dit coördinatenstelsel verandert de bewegingstoestand van een waarnemer niet, en brengt dus geen verandering in het waarnemingsreferentiekader van de waarnemer met zich mee. Dit standpunt is ook elders terug te vinden. Wat niet wil zeggen dat sommige coördinatenstelsels voor sommige waarnemingen een betere keuze kunnen zijn dan andere.

• De keuze van wat men wil meten en met welk waarnemingsapparaat staat los van de bewegingstoestand van de waarnemer en de keuze van het coördinatenstelsel.

Hier volgt een citaat dat van toepassing is op bewegende waarnemingskaders R {\displaystyle {\mathfrak {R}}

en diverse bijbehorende Euclidische drie-ruimte coördinatenstelsels :

We introduceren eerst het begrip referentiekader, dat op zijn beurt samenhangt met het idee van waarnemer: het referentiekader is in zekere zin de “Euclidische ruimte die door de waarnemer wordt gedragen”. Laten we een meer wiskundige definitie geven:… het referentiekader is… de verzameling van alle punten in de Euclidische ruimte met de starre lichaamsbeweging van de waarnemer. Het referentiekader, aangeduid met R {R}}

, wordt gezegd mee te bewegen met de waarnemer…. De ruimtelijke posities van de deeltjes worden gelabeld ten opzichte van een kader R {\displaystyle {\mathfrak {R}}}

door een coördinatenstelsel R met oorsprong O vast te stellen. De bijbehorende verzameling assen, die de starre lichaamsbeweging van het frame R {\displaystyle {\mathfrak {R}}}

, kan worden beschouwd als een fysische realisatie van R {\displaystyle {\mathfrak {R}}

. In een frame R {\displaystyle {\mathfrak {R}}

, worden coördinaten veranderd van R naar R′ door op elk tijdstip dezelfde coördinatentransformatie uit te voeren op de componenten van intrinsieke objecten (vectoren en tensoren) die zijn ingevoerd om fysische grootheden in dit kader weer te geven.

en dit over het nut van het scheiden van de begrippen R {R}}

en :

Zoals Brillouin opmerkte, moet er een onderscheid worden gemaakt tussen wiskundige coordinatenverzamelingen en fysische referentiekaders. De onwetendheid van een dergelijk onderscheid is de bron van veel verwarring… de afhankelijke functies, zoals bijvoorbeeld snelheid, worden gemeten ten opzichte van een fysisch referentiekader, maar men is vrij om elk wiskundig coördinatenstelsel te kiezen waarin de vergelijkingen zijn gespecificeerd.

en dit, ook over het onderscheid tussen R {{}}}

en :

Het idee van een referentiekader is eigenlijk iets heel anders dan dat van een coördinatenstelsel. Frames verschillen alleen wanneer ze verschillende ruimten (reeksen rustpunten) of tijden (reeksen gelijktijdige gebeurtenissen) definiëren. Dus de ideeën van een ruimte, een tijd, van rust en gelijktijdigheid, gaan onlosmakelijk samen met die van kader. Een loutere verschuiving van de oorsprong, of een zuiver ruimtelijke draaiing van ruimtecoördinaten resulteert echter in een nieuw coördinatenstelsel. Frames komen dus op zijn best overeen met klassen van coördinatenstelsels.

en van J. D. Norton:

In de traditionele ontwikkelingen van de speciale en algemene relativiteit is het gebruikelijk geweest geen onderscheid te maken tussen twee heel verschillende ideeën. Het eerste is het begrip coördinatenstelsel, dat eenvoudigweg wordt opgevat als de soepele, inverteerbare toewijzing van vier getallen aan gebeurtenissen in ruimtetijdbuurten. Het tweede, het referentiekader, verwijst naar een geïdealiseerd systeem dat wordt gebruikt om dergelijke getallen toe te wijzen. Om onnodige beperkingen te vermijden, kunnen wij deze ordening scheiden van metrische begrippen. Van bijzonder belang voor onze doeleinden is dat elk referentiekader een bepaalde bewegingstoestand heeft bij elke gebeurtenis in de ruimtetijd. Binnen de context van de speciale relativiteit en zolang wij ons beperken tot referentiekaders in traagheidsbeweging, hangt er weinig van belang af van het verschil tussen een inertiaal referentiekader en het inertiaal coördinatenstelsel dat het induceert. Deze comfortabele omstandigheid houdt onmiddellijk op zodra we referentiekaders in niet-uniforme beweging gaan beschouwen, zelfs binnen de speciale relativiteit.

De discussie wordt door Brading en Castellani verder gevoerd dan eenvoudige ruimte-tijd coördinatenstelsels. Uitbreiding tot coördinatenstelsels met behulp van veralgemeende coördinaten ligt ten grondslag aan de Hamiltoniaanse en Lagrangiaanse formuleringen van de kwantumveldentheorie, de klassieke relativistische mechanica en de kwantumzwaartekracht.

CoördinatenstelselsEdit

Een waarnemer O, die zich bevindt bij de oorsprong van een lokale verzameling coördinaten – een referentiekader F. De waarnemer in dit kader gebruikt de coördinaten (x, y, z, t) om een gebeurtenis in de ruimtetijd te beschrijven, weergegeven als een ster.

Hoewel de term “coördinatenstelsel” vaak wordt gebruikt (vooral door natuurkundigen) in een niet-technische betekenis, heeft de term “coördinatenstelsel” wel degelijk een precieze betekenis in de wiskunde, en soms is dat ook wat de natuurkundige bedoelt.

Een coördinatenstelsel in de wiskunde is een facet van de meetkunde of van de algebra, in het bijzonder een eigenschap van manifolds (bijvoorbeeld, in de natuurkunde, configuratieruimten of faseruimten). De coördinaten van een punt r in een n-dimensionale ruimte zijn eenvoudigweg een geordende verzameling van n getallen:

r = .

In een algemene Banach-ruimte kunnen deze getallen (bijvoorbeeld) coëfficiënten zijn in een functionele uitbreiding zoals een Fourier-reeks. In een natuurkundig probleem kunnen het ruimtetijdcoördinaten zijn of amplitudes van normale modi. In een robotontwerp kunnen het hoeken van relatieve rotaties, lineaire verplaatsingen of vervormingen van gewrichten zijn. We zullen hier veronderstellen dat deze coördinaten kunnen worden gerelateerd aan een Cartesisch coördinatenstelsel door een stel functies:

x j = x j ( x , y , z , … ) , j = 1 , … , n , {{j}=x^{j}(x,\ y,\ z,\ n ),\quad j=1,\ n,}

waarbij x, y, z, enz. de n cartesische coördinaten van het punt zijn. Gegeven deze functies, worden coördinaten oppervlakken gedefinieerd door de relaties:

x j ( x , y , z , … ) = c o n s t a n t , j = 1 , … , n . x^{j}(x,y,z,punten )= {constant} , j=1,punten,n.}

De snijpunten van deze oppervlakken definiëren coördinatenlijnen. In een willekeurig gekozen punt definiëren de raaklijnen aan de snijdende coördinatenlijnen in dat punt een verzameling basisvectoren {e1, e2, …, en} in dat punt. Dat wil zeggen:

e i ( r ) = lim ϵ → 0 r ( x 1 , … , x i + ϵ , … , x n ) – r ( x 1 , … , x i , … , x n ) ϵ , i = 1 , … , n , {Stijl ^mathbf {e} _{i}(\mathbf {r} )=lim _{\epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},x^{i}+\epsilon,x^{n}rechts)-\mathbf {r} \links(x^{1},x^{i},\ x^{i},\ x^{n}rechts)}{\epsilon }},\quad i=1,\ x^{n},\ n,}

die genormaliseerd kan worden om een lengte-eenheid te hebben. Voor meer details zie kromlijnige coördinaten.

Coordinaatoppervlakken, coördinaatlijnen, en basisvectoren zijn componenten van een coördinatenstelsel. Als de basisvectoren in elk punt orthogonaal zijn, is het coördinatenstelsel een orthogonaal coördinatenstelsel.

Een belangrijk aspect van een assenstelsel is de metrische tensor gik, die de booglengte ds in het assenstelsel bepaalt in termen van de coördinaten:

( d s ) 2 = g i k d x i d x k , {{{ik} (ds)^{2}=g_{ik} dx^{i} dx^{k},}

waarbij herhaalde indices bij elkaar worden opgeteld.

Zoals uit deze opmerkingen blijkt, is een assenstelsel een wiskundige constructie, onderdeel van een axiomatisch systeem. Er is geen noodzakelijk verband tussen coördinatenstelsels en fysische beweging (of enig ander aspect van de werkelijkheid). Coördinatenstelsels kunnen echter tijd als coördinaat bevatten, en kunnen worden gebruikt om beweging te beschrijven. Zo kunnen Lorentz-transformaties en Galileï-transformaties worden gezien als coördinatentransformaties.

Algemene en specifieke onderwerpen van coördinatenstelsels kunnen worden gevolgd via de Zie ook-links hieronder.

ReferentiekadersEdit

Drie referentiekaders in de speciale relativiteit. Het zwarte frame is in rust. Het geprimede frame beweegt met 40% van de lichtsnelheid, en het dubbele geprimede frame met 80%. Let op de schaarvormige verandering naarmate de snelheid toeneemt.

Een waarnemingskader, vaak referentiekader, referentiekader of gewoon kader genoemd, is een natuurkundig concept dat betrekking heeft op een waarnemer en de bewegingstoestand van de waarnemer. Wij nemen hier het standpunt over van Kumar en Barve: een waarnemingskader wordt alleen gekenmerkt door zijn bewegingstoestand. Er bestaat echter geen eensgezindheid op dit punt. In de speciale relativiteit wordt soms onderscheid gemaakt tussen een waarnemer en een frame. Volgens deze opvatting is een kader een waarnemer plus een coördinatenrooster dat geconstrueerd is als een orthonormale rechtshandige verzameling van ruimtelijke vectoren loodrecht op een tijdsvector. Zie Doran. Deze beperkte opvatting wordt hier niet gebruikt, en wordt zelfs in discussies over relativiteit niet universeel aanvaard. In de algemene relativiteit is het gebruik van algemene coördinatenstelsels gebruikelijk (zie bijvoorbeeld de Schwarzschild oplossing voor het gravitatieveld buiten een geïsoleerde bol).

Er zijn twee soorten waarnemingsreferentiekaders: inertiële en niet-inertiële. Een inertiaal referentiekader wordt gedefinieerd als een kader waarin alle natuurkundige wetten hun eenvoudigste vorm aannemen. In de speciale relativiteit zijn deze kaders met elkaar verbonden door Lorentz-transformaties, die worden geparametriseerd door de snelheid. In de Newtoniaanse mechanica vereist een beperktere definitie alleen dat de eerste wet van Newton geldt; dat wil zeggen dat een Newtoniaans inertiaalkader een kader is waarin een vrij deeltje zich in een rechte lijn met constante snelheid voortbeweegt, of in rust is. Deze kaders zijn met elkaar verbonden door Galileïtransformaties. Deze relativistische en Newtonse transformaties worden uitgedrukt in ruimten van algemene dimensie in termen van representaties van de Poincaré-groep en van de Galileïsche groep.

In tegenstelling tot het inertiale frame is een niet-inertiaal referentiekader er een waarin fictieve krachten moeten worden ingeroepen om waarnemingen te verklaren. Een voorbeeld is een referentiekader met het middelpunt op een punt op het aardoppervlak. Dit referentiekader draait rond het middelpunt van de Aarde, waardoor de fictieve krachten worden geïntroduceerd die bekend staan als de Corioliskracht, de centrifugale kracht en de zwaartekracht. (Al deze krachten, inclusief de zwaartekracht, verdwijnen in een werkelijk inertiaal referentiekader, dat er een is van vrije val.)

MetingsapparatuurEdit

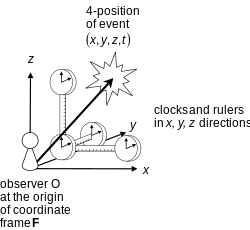
Een ander aspect van een referentiekader is de rol van de meetapparatuur (bijvoorbeeld klokken en staven) die aan het kader is bevestigd (zie Norton-citaat hierboven). Deze vraag wordt in dit artikel niet behandeld, en is vooral van belang in de kwantummechanica, waar de relatie tussen waarnemer en meting nog ter discussie staat (zie meetprobleem).

In natuurkundige experimenten wordt het referentiekader waarin de meetapparatuur in het laboratorium in rust is, gewoonlijk het laboratoriumkader of kortweg “labkader” genoemd. Een voorbeeld hiervan is het frame waarin de detectoren van een deeltjesversneller in rust zijn. In sommige experimenten is het laboratoriumframe een inertiaalframe, maar dat hoeft niet (bijvoorbeeld het laboratorium op het aardoppervlak in veel natuurkundige experimenten is niet inertiaal). In deeltjesfysica-experimenten is het vaak nuttig om energieën en impulsmomenten van deeltjes te transformeren van het laboratoriumframe waarin ze gemeten worden, naar het centrum van impulsmomentframe “COM frame” waarin berekeningen soms vereenvoudigd worden, omdat potentieel alle kinetische energie die nog aanwezig is in het COM frame gebruikt kan worden voor het maken van nieuwe deeltjes.

In dit verband kan worden opgemerkt dat de klokken en staven die vaak worden gebruikt om de meetapparatuur van waarnemers in gedachten te beschrijven, in de praktijk worden vervangen door een veel gecompliceerdere en indirecte metrologie die samenhangt met de aard van het vacuüm, en gebruik maakt van atoomklokken die werken volgens het standaardmodel en die moeten worden gecorrigeerd voor gravitationele tijddilatatie. (Zie seconde, meter en kilogram).

In feite was Einstein van mening dat klokken en staven slechts nuttige meetinstrumenten waren en vervangen moesten worden door fundamentelere entiteiten, gebaseerd op bijvoorbeeld atomen en moleculen.