Inleiding
Deze pagina behandelt hoofdspanningen en -rek. Hoewel we de vele verschillende definities van spanning en rek nog niet hebben besproken, is het in feite zo dat alles wat hier besproken wordt van toepassing is ongeacht het type spanning of rekstensor. Bijvoorbeeld, als je de hoofdwaarden van een Cauchy spanningstensor berekent, dan krijg je de hoofdspanningen van Cauchy. De hoofdwaarden van een Groene spanningstensor zullen hoofd-Groene spanningen zijn.
Alles hieronder volgt uit twee feiten: Ten eerste, de input spannings- en rektrekspanningen zijn symmetrisch.Ten tweede, de coördinatentransformaties die hier besproken worden zijn toepasbaar op spannings- en rektrekspanningen (dat zijn ze inderdaad).
We zullen het eerst over spanning hebben, dan over rek.
2-D hoofdspanningen

In 2-D, zijn de transformatievergelijkingen
Dit zijn de uitgebreide vormen van \(\boldsymbol{\sigma}’ = {\bf Q} \boldsymbol{\sigma} \boldsymbol{\sigma} \boldsymbol{\bf Q}^T}) in 2-D.Ze kunnen ook worden afgeleid uit een krachtenevenwicht van de hier getoonde figuur. Het is interessant dat spanning wordt gekarakteriseerd als een tensor omdat het de transformatievergelijking volgt. Maar dit is vooral een wiskundig argument, en het zou weinig gewicht in de schaal leggen als het niet verbonden was met de fysica van het krachtenevenwicht. Het feit dat de coördinatentransformatievergelijking het krachtenevenwicht goed weergeeft bij verschillende oriëntaties is wat het relevant maakt.
De hoofdspanningen zijn de corresponderende normaalspanningen onder een hoek, waarbij de afschuifspanning, nul is.
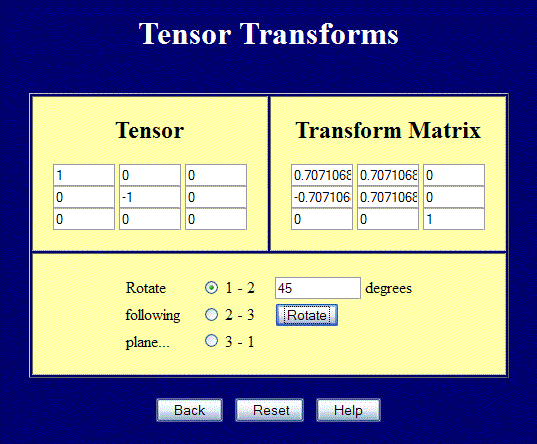
Deze pagina voert volledige 3D tensortransformaties uit, maar kan nog steeds gebruikt worden voor 2D problemen. Voer waarden in in de bovenste linker 2×2 posities en draai in het 1-2 vlak om transformaties in 2-D uit te voeren. De schermafbeelding hieronder toont een geval van zuivere afschuiving, 45° geroteerd om de hoofdspanningen te verkrijgen. Merk ook op hoe de Q-matrix transformeert.
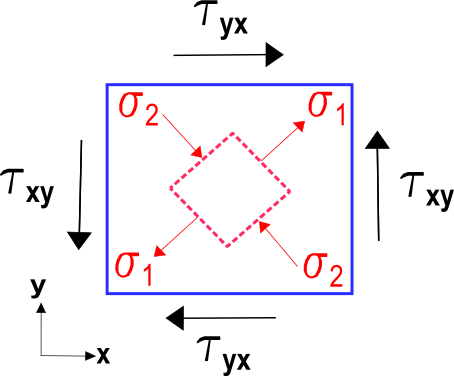
De figuur hieronder toont de spanningen die overeenkomen met het pure afschuiving geval in het tensor transform webpagina voorbeeld. Het blauwe vierkant uitgelijnd met de assen ondergaat duidelijk afschuiving.Maar het rode vierkant ingeschreven in het grotere blauwe vierkant ziet alleen eenvoudige spanning en compressie.Dit zijn de hoofdwaarden van het pure afschuiving geval in het globale coördinatenstelsel.
In 2-D kan de hoofdspanningsrichting, (\theta_P\), worden berekend door \tau’_{xy} = 0) in de bovenstaande afschuifvergelijking te zetten en op te lossen voor \(\theta_P\) om \(\theta_P\) te krijgen, de hoofdspanningshoek. ls we deze waarde voor (\theta_P\) weer in de vergelijkingen voor de normaalspanningen invoeren, krijgen we de hoofdwaarden. Deze worden geschreven als ⁰max} en ⁰min}, of als ⁰_1) en ⁰2).
Ze zouden ook kunnen worden verkregen door \(\boldsymbol{sigma}’ = {\bf Q} \cdot \boldsymbol{sigma} \cdot {\bf Q}^T) te gebruiken met \({\bf Q}) gebaseerd op \(\theta_P\).
3-D hoofdspanningen
Coördinatentransformaties in 3-D zijn
= \leftleftleft]
De tweede ({\bf Q}}) matrix is weer de getransponeerde van de eerste.
Deze pagina voert tensor-transformaties uit.
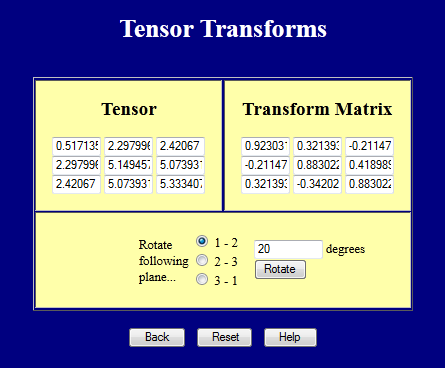
En deze pagina berekent hoofdwaarden (eigenwaarden)en hoofdrichtingen (eigenvectoren).
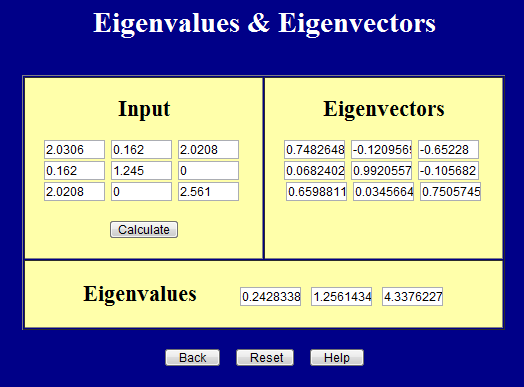
Het is belangrijk om te onthouden dat de ingangen van beide pagina’s symmetrisch moeten zijn. In feite dwingen beide pagina’s dit af.
De eigenwaarden hierboven kunnen in matrixvorm worden geschreven als
2-D hoofdspanningen
De mechanica voor het berekenen van hoofdspanningen is identiek aan die voor het berekenen van hoofdspanningen. De enige potentiële valkuil is dat de vergelijkingen altijd werken op de helft van de schuifwaarden, ⁰(⁰gamma / 2⁰).
In 2D zijn de transformatievergelijkingen ⁰(⁰gamma / 2⁰) om te benadrukken dat de helft van alle schuifwaarden wordt gebruikt in de transformatievergelijkingen.
Deze pagina voert volledige 3D tensor transformaties uit, maar kan nog steeds worden gebruikt voor 2D problemen. Voer waarden in in de bovenste linker 2×2 posities en draai in het 1-2 vlak om transformaties in 2-D uit te voeren. De schermafbeelding hieronder toont een geval van zuivere afschuiving, 45° geroteerd om de hoofdspanningen te verkrijgen. Merk ook op hoe de Q-matrix transformeert.

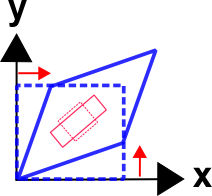
De figuur hieronder toont de vervormde vormen die overeenkomen met het pure afschuiving geval in het tensor transform webpagina voorbeeld. Het blauwe vierkant uitgelijnd met de assen ondergaat duidelijk afschuiving.Maar het rode vierkant ingeschoven in het grotere blauwe vierkant ziet alleen eenvoudige spanning en compressie.Dit zijn de hoofdwaarden van de pure afschuiving vervorming in het globale coördinatenstelsel.
In 2-D kan de hoofdverdraaiingsrichting, (\theta_P\), worden berekend door \(\gamma_{xy} = 0) in de bovenstaande afschuifvergelijking te zetten en op te lossen voor \(\theta_P\) om \(\theta_P\), de hoofdverdraaiingshoek, te krijgen. ls we deze waarde voor (\theta_P\) weer in de vergelijkingen voor de normaalspanningen invoegen, krijgen we de hoofdwaarden. Deze worden geschreven als \(\epsilon_{max}) en \(\epsilon_{min}), of als \(\epsilon_1) en \(\epsilon_2).
Ze zouden ook verkregen kunnen worden door \({\bf E}’ = {\bf Q} \cdot {\bf E} \cdot {\bf Q}^T) te gebruiken met \({\bf Q}) gebaseerd op \(\theta_P\).
3-D hoofdspanningen
Coordinaattransformaties in 3-D zijn
= \leftleftleftleft]
De tweede ({\bf Q}}) matrix is weer de getransponeerde van de eerste.
Deze pagina voert tensor-transformaties uit.

En deze pagina berekent hoofdwaarden (eigenwaarden)en hoofdrichtingen (eigenvectoren).

Het is belangrijk om te onthouden dat de ingangen van beide pagina’s symmetrisch moeten zijn. In feite dwingen beide pagina’s dit af.
De eigenwaarden hierboven kunnen in matrixvorm worden geschreven als
Samenvatting
Dit principe van invariante grootheden onder coördinatentransformaties is in feite universeel voor alle matrices die symmetrisch zijn en worden getransformeerd volgens
waarbij ({{{bf A}}) “elke symmetrische matrix” is.
En vergeet niet dat het product van elke matrix met zijn getransponeerde altijd een symmetrisch resultaat is, dus dit resultaat zou in aanmerking komen. Dit is vooral van belang voor de invariant van de wet van Mooney-Rivlin voor het gedrag van rubber. De wet van Mooney-Rivlin en de coëfficiënten zullen op deze pagina besproken worden. Als extra teaser zullen we zien dat de 3de invariant van de wet van Mooney-Rivlin voor rubber altijd gelijk is aan 1 omdat rubber onsamendrukbaar is. Dus niet alleen is het een constante, onafhankelijk van coördinatentransformaties, maar het is zelfs een constante waarde, altijd gelijk aan 1, onafhankelijk van coördinatentransformaties en de staat van vervorming.