Eindige toestandsmachines

Deterministische eindige automaten

Een deterministische eindige automaat (DFA) wordt beschreven door een tupel van vijf elementen: (Q,Σ,δ,q0,F)(Q, Σ,δ,q0,F)(Q, ΣSigma, Σdelta, q_0, F)(Q,Σ,δ,q0,F).

QQQ = een eindige verzameling toestanden

ΣSigmaΣ = een eindig, niet-leeg invoeralfabet

δdeltaδ = een reeks overgangsfuncties

q0q_0q0 = de begintoestand

FFF = de verzameling toestanden

Er moet precies één overgangsfunctie zijn voor elk invoersymbool in ΣSigmaΣ van elke toestand.

DFA’s kunnen worden voorgesteld met diagrammen van deze vorm:

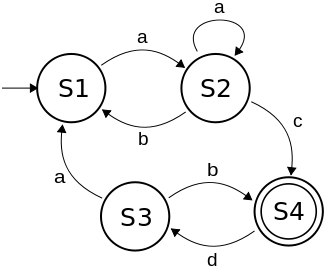
Hier volgt een DFA-diagram dat een paar eenvoudige bewegingen beschrijft die een personage in een videospel kan doen: staan, rennen, en springen. De knoppen die een speler kan gebruiken om dit specifieke personage te besturen zijn “Omhoog”, “A”, of de speler kan op geen enkele knop drukken.

Gebruik makend van het toestandsdiagram voor het videospelfiguur hierboven, beschrijf hoe een speler zijn personage kan besturen om van staan naar rennen naar springen te gaan.

Toon antwoord

In de staande status kan de speler op niets drukken en in de staande status blijven, vervolgens, om over te gaan naar de lopende status, moet de gebruiker op de “Omhoog”-knop drukken. In de lopende status kan de gebruiker zijn personage blijven laten lopen door op de “Omhoog” toets te drukken, en dan, om naar de spring status over te gaan, moet de gebruiker op “A” drukken.

Teken een diagram voor een DFA die de volgende taal herkent: De taal van alle strings die eindigen op een 1.

Toon antwoord

Nondeterministische Eindige Automata

QQQ = een eindige verzameling toestanden

ΣSigmaΣ = een eindig, niet-leeg invoeralfabet

δdeltaδ = een reeks overgangsfuncties

q0q_0q0 = de begintoestand

FFF = de verzameling toestanden

In tegenstelling tot DFA’s hoeven NDFA’s geen overgangsfuncties te hebben voor elk symbool in ΣSigmaΣ, en er kunnen meerdere overgangsfuncties in dezelfde toestand zijn voor hetzelfde symbool. Bovendien kunnen NDFA’s nulovergangen gebruiken, die worden aangeduid met ϵ\epsilonϵ. Met null overgangen kan de machine van de ene toestand naar de andere springen zonder een symbool te hoeven lezen.

Een NDFA accepteert een string xxx als er een pad bestaat dat compatibel is met die string en dat eindigt in een accept state.

NDFA’s kunnen worden voorgesteld door diagrammen van deze vorm:

bron

Beschrijf de taal die de NDFA hierboven herkent.

Toon antwoord

De NDFA hierboven herkent strings die eindigen op “10” en strings die eindigen op “01.”

Status aaa is de begintoestand, en van daaruit kunnen we een string maken met hoeveel 1’s en 0’s dan ook, in willekeurige volgorde, en dan overgaan naar toestand bbb of toestand eee, of we kunnen onmiddellijk overgaan naar toestand bbb of toestand eee. In elk geval zal de NDFA enkel een string accepteren die toestand ddd of toestand ggg bereikt. Om status ddd of status ggg te bereiken, moet de string eindigen met een “01” (voor status ddd) of een “10” (voor status ggg).

De volgende strings worden bijvoorbeeld allemaal herkend door deze NDFA.

• 00000000010
• 10
• 01
• 1111101

Teken een diagram voor de NDFA die de volgende taal beschrijft: De taal van alle strings die eindigen op een 1.

Toon antwoord