De efficiëntie van een algoritme hangt af van de hoeveelheid tijd, opslag en andere middelen die nodig zijn om het algoritme uit te voeren. De doelmatigheid wordt gemeten met behulp van asymptotische notaties.
Een algoritme zal niet altijd even goed presteren voor verschillende soorten invoer. Met de toename van de ingangsgrootte zal de prestatie veranderen.
De studie van de verandering in prestatie van het algoritme met de verandering in de orde van de ingangsgrootte wordt asymptotische analyse gedefinieerd.
Asymptotische notaties
Asymptotische notaties zijn de wiskundige notaties die worden gebruikt om de looptijd van een algoritme te beschrijven wanneer de ingang naar een bepaalde waarde of een grenswaarde neigt.
Voorbeeld: In bubble sort, wanneer de input array al gesorteerd is, is de tijd die het algoritme nodig heeft lineair i.e. het beste geval.
Maar, wanneer de input array in omgekeerde toestand is, neemt het algoritme de maximale tijd (kwadratisch) om de elementen te sorteren i.e. het slechtste geval.
Wanneer de input array noch gesorteerd noch in omgekeerde volgorde is, dan neemt het algoritme gemiddelde tijd. Deze looptijden worden aangeduid met asymptotische notaties.
Er zijn in hoofdzaak drie asymptotische notaties:
- Big-O notatie
- Omega notatie
- Theta notatie
Big-O notatie (O-notatie)
Big-O notatie geeft de bovengrens van de looptijd van een algoritme weer. Het geeft dus de worst-case complexiteit van een algoritme.
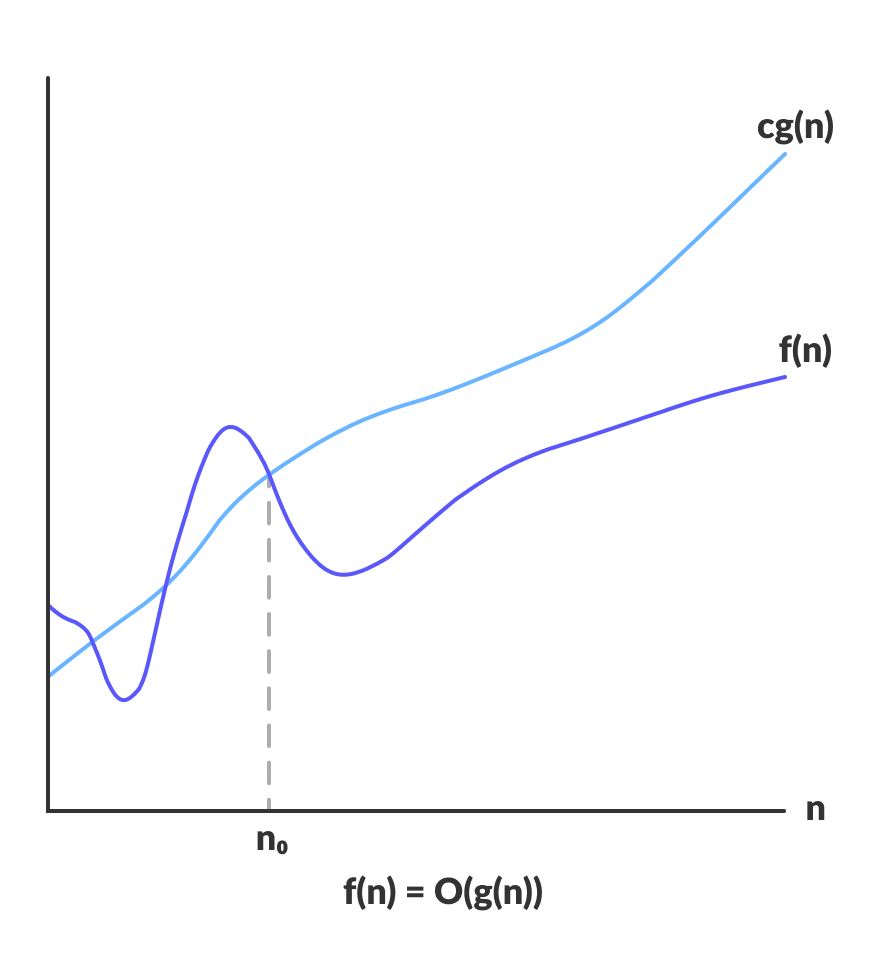
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
De bovenstaande uitdrukking kan worden beschreven als een functie f(n) behoort tot de verzameling O(g(n)) als er een positieve constante c bestaat zodat deze tussen 0 en cg(n) ligt, voor voldoende grote n.
Voor elke waarde van n overschrijdt de looptijd van een algoritme niet de door O(g(n)) gegeven tijd.
Omdat het de slechtst denkbare looptijd van een algoritme geeft, wordt het veel gebruikt om een algoritme te analyseren, omdat we altijd geïnteresseerd zijn in het slechtst denkbare scenario.
Omega-notatie (Ω-notatie)
Omega-notatie geeft de ondergrens van de looptijd van een algoritme. Het geeft dus de best-case complexiteit van een algoritme.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
De bovenstaande uitdrukking kan worden beschreven als een functie f(n) behoort tot de verzameling Ω(g(n)) als er een positieve constante c bestaat zodanig dat deze boven cg(n) ligt, voor voldoende grote n.
Voor elke waarde van n is de minimale tijd die het algoritme nodig heeft gegeven door Omega Ω(g(n)).
Theta-notatie (Θ-notatie)
Theta-notatie omsluit de functie van boven en van beneden. Omdat het de boven- en ondergrens van de looptijd van een algoritme weergeeft, wordt het gebruikt voor het analyseren van de gemiddelde-case complexiteit van een algoritme.
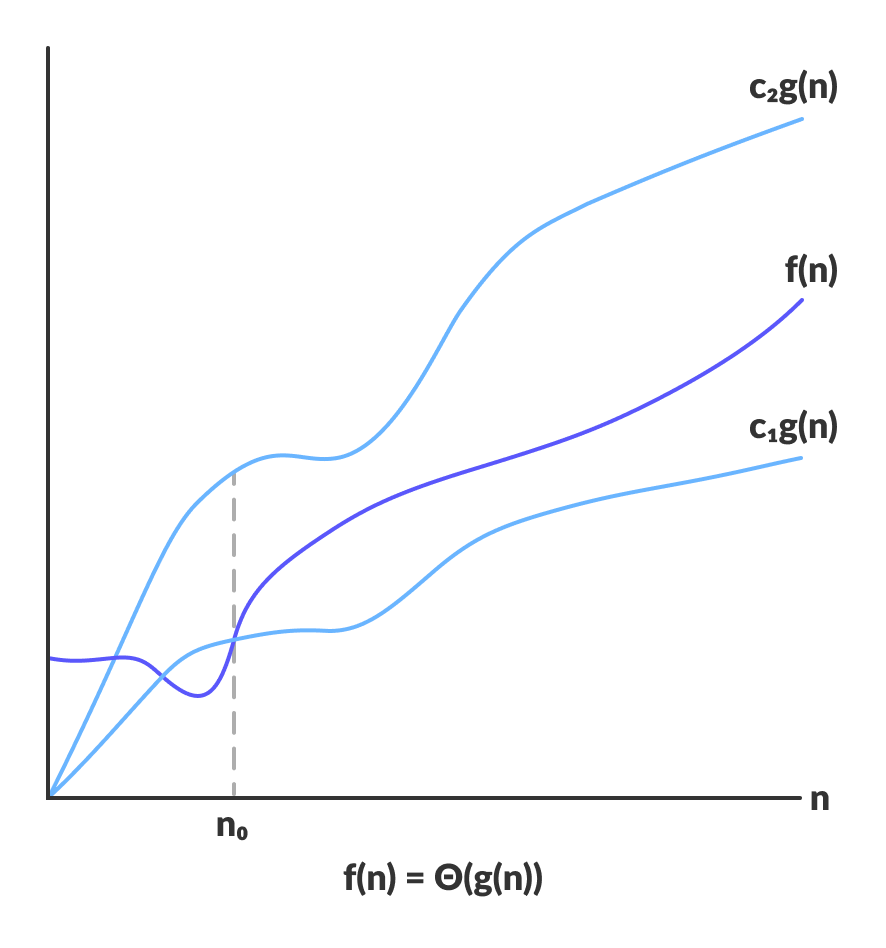
Voor een functie g(n)Θ(g(n)) wordt gegeven door de relatie:
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
De bovenstaande uitdrukking kan worden beschreven als een functie f(n) behoort tot de verzameling Θ(g(n)) als er bestaan positieve constanten c1 en c2 bestaan, zodat zij ingeklemd kan worden tussen c1g(n) en c2g(n), voor voldoende grote n.
Als een functie f(n) ergens tussen c1g(n) en c2g(n) ligt voor alle n ≥ n0, dan wordt f(n) asymptotisch tight bound genoemd.