
Ik zal eerlijk zijn. Ik doe al jaren serieus aan calculus dan ik wil toegeven. Soms moet je in de natuurkunde gewoon dingen integreren. Dat gebeurt nu eenmaal.
Toen ik echter mijn zoon hielp met zijn wiskundeles, begon ik me te realiseren – wat is er in vredesnaam aan de hand met integreren? Ik heb het gevoel dat ik derivaten heel goed begrijp – maar bij integratie gebeuren er rare dingen.
Wel, je zult dingen nooit begrijpen totdat je ze in hun basisstukjes uit elkaar haalt. Dus, dat is wat ik ga doen. Ik ga de oppervlakte onder een kromme op drie verschillende manieren vinden.
Area using summation notation
Dit is het makkelijkst te begrijpen, maar het moeilijkst uit te rekenen. Oh wacht! Waarom zoeken we de oppervlakte onder een kromme? OK, wacht even – mijn voorbeeld aan het eind moet helpen.
Het basisidee is dus om een gebied op te delen in N rechthoeken (waarbij N gewoon een getal is). Ik kan dan de oppervlakte van elke rechthoek vinden en ze bij elkaar optellen om de totale oppervlakte te krijgen. Hoe meer stukken ik opdeel, hoe beter het antwoord – dus ik zal een uitdrukking schrijven voor deze oppervlakte en de limiet nemen als het aantal stukken naar oneindig gaat.

De oppervlakte zou dan worden berekend als:
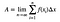
Er volgt nog een heleboel – en het wordt een beetje eentonig. Maar je MOET dit doornemen om alles volledig te begrijpen. Hier is een video waarin ik je erdoorheen help.
Als u een functie gebruikt:
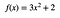
De oppervlakte van x = 1 tot x =2 is 9 (wat de eenheden ook zouden moeten zijn – ik ben geen wiskundige, dus het stoort me om de eenheden weg te laten).
Area using anti-derivatives
Er is een trucje. Het is een geweldige truc. Je kunt de oppervlakte onder een kromme schrijven als een bepaalde integraal (waarbij de integraal een oneindige som is van oneindig kleine stukjes – net als de sommatie-notatie).
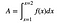
Nu de gekke dingen. GEK. Het blijkt dat de oppervlakte de anti-afgeleide is van f(x). Als je even stopt, zul je zien dat dat wild is. Gek wild. Als de afgeleide iets zegt over de helling van een kromme, zegt het tegengestelde van de afgeleide dan iets over de oppervlakte onder de kromme?
Jup. Het is de fundamentele stelling van calculus. Hier is mijn uitleg (ja, er komen een heleboel video’s in deze post en je bent VERPLICHT om ze allemaal te bekijken.
Eigenlijk is er nog iets belangrijks hier. De bepaalde integraal van x = 1 naar x = 2 is het verschil in de oppervlaktefunctie A(2) en A(1). Ik zal daar niet in detail op ingaan, want ik ben nog steeds verbijsterd over dat anti-afgeleide gedoe.
Maar hier is de oppervlakte onder dezelfde functie, maar dan met integratie.
Ja. Je krijgt hetzelfde eindresultaat. Oppervlakte = 9 kippen² (ik heb de oppervlakte-eenheden toegevoegd).
Oppervlakte met behulp van numerieke berekeningen
Nu komen we bij het leuke werk. Wat als ik de oppervlakte onder een kromme zou vinden door de oppervlakte van een aantal rechthoeken bij elkaar op te tellen? Oh wacht…dat heb ik al gedaan in de eerste methode. Maar wat dacht je hiervan – ik doe geen oneindig aantal rechthoeken, ik doe gewoon een groot aantal rechthoeken? Dat is precies waar het bij een numerieke berekening om gaat.
Natuurlijk, als ik een gebied in 100 stukken breek, moet ik 100 reeksen oppervlakteberekeningen doen. Wil iemand dat echt doen? Nee – niemand denkt dat dat leuk zou zijn. Maar weet je wie dat niet kan schelen? Computers (elektronische computers).
Ja, we kunnen een computer deze reeks berekeningen laten doen. We hoeven het alleen maar wat instructies te geven en dan gaat het zijn werk doen. Het zal geweldig zijn. Hier is het basisrecept dat hij zal gebruiken.
- Bepaal in hoeveel stukken je de kromme wilt breken. Wat dacht je van 100? Met deze waarde en de begin- en eind x-waarde kun je de breedte van elke rechthoek berekenen (Δx).
- Zet de oppervlakte op nul (kippen²). We gaan deze waarde steeds aanvullen, maar het moet ergens beginnen.
- Begin met de begin x-waarde (in het voorbeeld dat ik heb gebruikt – dat is x = 1).
- Bereken de hoogte van de rechthoek. Dit is f(x) bij de huidige x-waarde.
- Vind de oppervlakte van deze rechthoek en tel die op bij de totale oppervlakte.
- Verplaats naar de volgende x-waarde en herhaal tot je bij de laatste x bent.
Dat is zo eenvoudig dat zelfs een computer het zou kunnen. OK, ik maak maar een grapje. Sommige van mijn beste vrienden zijn computers.
Hier is de code voor deze berekening in python (hier is een link naar de echte code).
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
Met N = 100 krijg ik een oppervlakte van 8,95505 – dat is NIET precies 9 kippen², maar het komt aardig in de buurt. Dichtbij genoeg voor de meeste vierkante kip berekeningen.
Een paar snelle opmerkingen over deze code.
- Het leek me leuk om van de functie een echte python functie te maken (dat is het
def f(t):gedeelte. - Ik bereken eerst de oppervlakte van het kleine rechthoekje (dA) en tel die dan op bij de totale oppervlakte.
- Deze methode heeft eigenlijk rechthoeken op een rij met de functie aan de linkerkant van de bovenkant van de rechthoek. Je zou het ook met de rechterkant kunnen doen.
- Ik heb hier ook een video voor gemaakt. Maar je bent niet verplicht die te bekijken – ik heb het hier grotendeels al uitgelegd.
Wat als je geen wiskundige functie hebt?
Laat me je in de volgende situatie plaatsen. U zit in een auto die rijdt en u kunt ALLEEN de snelheidsmeter zien. U noteert elke seconde de snelheidswaarde (want u bent supersnelle notulist). Uiteindelijk stopt de auto en moet je achterhalen hoe ver je hebt afgelegd.
Hier is zoiets (met behulp van een Vernier karretje met een bewegingssensor – maar je krijgt het idee dat dit hetzelfde is als een echte auto).

OK – waarschuwing, Ik ga hier vals spelen. De Vernier track verzamelt positiegegevens op basis van deze lijnen op de track. Uit de positiegegevens, berekent het de snelheid. Dus, ik heb al de positie van de kar – maar laten we doen alsof het alleen de snelheid als functie van de tijd geeft. Misschien zou het er dan zo uitzien.

Zie. Dat is geen functie, dat is een ruimtestation. Nee, wacht – dat is van Star Wars. Maar toch, het is geen wiskundige functie. Het is gewoon data. Je kan de anti-afgeleide van data niet vinden (wel, niet met de normale regels en zo). Maar wacht! De numerieke integratie werkt prima.
Natuurlijk is er nog iets belangrijks hier. Het is het idee dat het gebied onder deze kromme iets reëels voorstelt. Stel je voor dat je een auto hebt die een bepaalde tijd met een constante snelheid rijdt. Je zou de verplaatsing vrij eenvoudig kunnen berekenen:
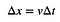
Als je een plot hebt van snelheid vs. tijd, zou deze constante snelheid eruit zien als een rechthoek. Ja, de oppervlakte van die rechthoek zou v*Δt zijn. Als het GEEN constante snelheid is, zou het gebied onder de snelheid-tijd grafiek nog steeds de verplaatsing zijn.
OK, nog een laatste video. Hier is mijn uitleg van de codering om dit verplaatsingsprobleem op te lossen.
Zorg ervoor dat je alle video’s bekijkt.