
正直に言います。 私は認めたくないほど何年も真剣に微積分をやっています。 物理学の世界では、どうしても物事を統合しなければならないことがあります。
しかし、息子の微積分の授業を手伝っていたときに、積分とはいったい何なのか、ということに気づきました。
しかし、息子の微積分の授業を手伝っているときに、「積分はいったいどうなっているんだろう」と気がつきました。微分についてはしっかり理解しているつもりですが、積分には奇妙な点があります。
さて、基本的な部分に分解しない限り、物事を理解することはできません。そこで、私がやろうとしていることは
和算表記を使った面積
これが一番わかりやすいですが、計算するのは一番難しいです。 あ、そうだ。 なぜ曲線の下の面積を求めるのでしょうか?
では、基本的なアイデアは、面積を N 個の長方形に分割することです (N は単なる数です)。 そして、各長方形の面積を求め、それらを合計して総面積を得ることができます。 分割数が多ければ多いほど、より良い答えが得られます。そこで、この面積を表す式を書き、分割数が無限大になったときの限界を見てみます。

すると、面積は次のように計算されます。
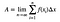
となります。
この後もいろいろあって、ちょっと面倒くさいですね。 しかし、全体を完全に理解するためには、これを必ず通過しなければなりません。 ここでは、私がその手順を説明するビデオをご紹介します。
関数を使用する場合。
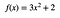
x = 1からx = 2までの面積は9(単位は何でもいいのですが、私は数学者ではありません。
x = 1 から x = 2 までの面積は 9 です。)
反微分を使った面積
コツがあります。 すごいトリックです。 曲線の下の面積を定積分として書くことができます (積分は無限に小さい断片の無限の和です – 和算表記のように)。
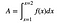
さて、とんでもないことをしますよ。 CRAZYです。 面積がf(x)の反微分であることがわかりました。 ちょっと立ち止まってみると、それはワイルドだということがわかります。 クレイジーワイルド。 微分が曲線の傾きについて何かを教えてくれるなら、微分の反対は曲線の下の面積について教えてくれるということですか? 微積分学の基本定理です。
実は、ここにはもう1つ重要なことがあります。 x = 1からx = 2までの定積分は、面積関数A(2)とA(1)の差になります。
しかし、ここでは、同じ関数の下の面積を積分で表しています。
はい、同じ最終結果が得られます。 Area = 9 chickens² (面積の単位を追加しました).
数値計算による面積
さて、いよいよ楽しい話になってきました。 たくさんの長方形の面積を足すことで、曲線の下の面積を求めたらどうでしょう? 待ってください、それは最初の方法ですでにやっています。 でも、無限の長方形を作るのではなく、たくさんの長方形を作るというのはどうでしょう?
もちろん、面積を100個に分割すると、面積計算を100セット行わなければなりません。 そんなことをしたいと思う人がいるでしょうか? いや、誰もそんなことが楽しいとは思っていないでしょう。 でも、そんなことを気にしない人がいるとしたら?
そう、コンピュータにこの一連の計算をさせることができるのです。 いくつかの指示を与えるだけで、あとは仕事をしてくれるのです。 それは素晴らしいことです。
- 曲線を何枚に分割するかを決めます。 100個ではどうでしょうか? これと開始と終了のx値で、各長方形の幅を計算します(Δx)。
- 面積をゼロに設定します(chickens²)。
- 初期の x 値 (使用した例では、x = 1) から始めます。
- 長方形の高さを計算します。
- 次の x 値に移動し、最後の x に到達するまで繰り返します。
とても簡単なので、コンピュータでもできるでしょう。 OK、私はただ楽しんでいるだけです。
以下は python でのこの計算のコードです (実際のコードへのリンクです)。
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
N = 100 の場合、8.95505 の面積が得られます – これは正確には 9 チキン² ではありませんが、かなり近い値です。
このコードに関する簡単なコメントをいくつか。
- この関数を実際の python 関数にするのは面白いと思いました (これは
def f(t):部分です)。 - まず、小さな長方形の面積 (dA) を計算し、それを全体の面積に加えます。
- この方法では、実際に長方形を並べて、その上の左側に関数を配置しています。 右側でもできますね。
- このためにビデオも作りました。
数学的な関数がない場合は?
次のような状況を想定してみましょう。 あなたは車に乗っていて、スピードメーターしか見えません。 あなたは毎秒、速度の値を書き留めています(あなたは超高速のメモ取りですから)。
以下にそのような例を示します (モーション センサー付きのバーニア カートを使用していますが、実際の車と同じであることがお分かりいただけると思います)。

OK – 警告。 ここでは不正行為をするつもりです。 バーニアトラックは、トラック上のこれらのラインに基づいて位置データを収集します。 そして、その位置データから速度を算出しています。 つまり、私はすでにカートの位置を知っています – しかし、時間の関数としての速度だけを与えると仮定してみましょう。 たぶん、次のようになるでしょう。

ほら。 それは機能ではなく、宇宙ステーションなんです。 いや、待てよ、それはスターウォーズからだ。 しかし、それでも数学的な関数ではありません。 ただのデータです。 データの反微分を見つけることはできません(まあ、普通のルールとかでは無理ですが)。 でも、待てよ!
もちろん、ここには他にも重要なことがあります。 それは、この曲線の下にあるものが現実の何かを表しているという考え方です。 ある一定の時間、一定の速度で動いている車があるとします。 かなり簡単に変位を計算することができます。
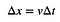
速度対時間のプロットがあれば、この一定の速度は次のようになります。 この一定の速度は、長方形のように見えます。 そう、その長方形の面積はv*Δtとなります。
OK、最後のビデオです。
必ずすべてのビデオを見てくださいね。