Introductory Chemistry – 1st Canadian Edition

By admin on

Learning Objectives

  1. 気体の運動分子論の背後にある主要な概念を述べる。
  2. 運動エネルギーと分子速度の関係を示す。
  3. 気体の法則を説明・予測するために運動分子論を適用する。

気体は、1600年代に開発された近代的な科学的手法を用いて研究された最初の物質の一つです。 気体の物理的挙動が共通していることを認識するのに時間はかからず、気体は1つの包括的な理論で記述できることが示唆されました。 気体の動力学的分子理論は、気体の物理的性質を分子レベルで理解するためのモデルである。

  1. 気体は、常にランダムに運動している粒子（分子または原子）から構成されています。
  2. 気体の粒子は、常にお互いに衝突しており、容器の壁にも衝突しています。
  3. 気体の粒子は小さく、気体の分子が占める総体積は容器の総体積に比べてごくわずかです。
  4. 気体の粒子間には相互作用力（引力や反発力）はありません。
  5. 気体粒子の平均運動エネルギーは気体の絶対温度に比例し、同じ温度の気体はすべて同じ平均運動エネルギーを持っています。

図6.

Figure 6-6

気体の運動分子論では、この物質の状態を、粒子間の距離が大きく、常に運動している小さな粒子で構成されていると説明しています。 気体が占める体積のほとんどは空虚な空間であるため、気体は密度が低く、適切な影響を受けて膨張または収縮することができます。 気体の粒子が常に動いているということは、それぞれの気体の粒子が動いて衝突することで、2つ以上の気体が常に混ざり合うことになる。

運動エネルギーと分子速度

気体の粒子は常に運動しており、運動している物体は運動エネルギー（Ek）を持っています。

Ek = 1/2 mu2

気体中の分子は全体として平均的な運動エネルギーを持っていますが、個々の分子には速度の分布があるため、運動エネルギーにも分布があります（図6.7「分子速度分布のイメージ」）。 この速度分布は、気相中の分子同士の衝突によって生じるものです。 これらの衝突は弾性的（エネルギーの正味の損失がない）ですが、衝突に関与した各分子の個々の速度は変化する可能性があります。

Figure 6.

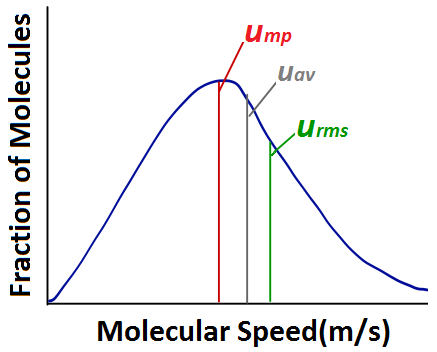
図6.7 スタイライズされた分子速度分布

分子速度の分布図を分析する際には、いくつかの一般的に使用される用語に精通しておく必要があります。 最確速度(ump)は、最大数の分子の速度で、分布のピークに相当します。 平均速度（uav）は、サンプル中のすべての気体分子の平均速度である。 二乗平均平方根（rms）速度（urms）は、サンプルの平均運動エネルギーと全く同じ運動エネルギーを持つ分子の速度に対応します。

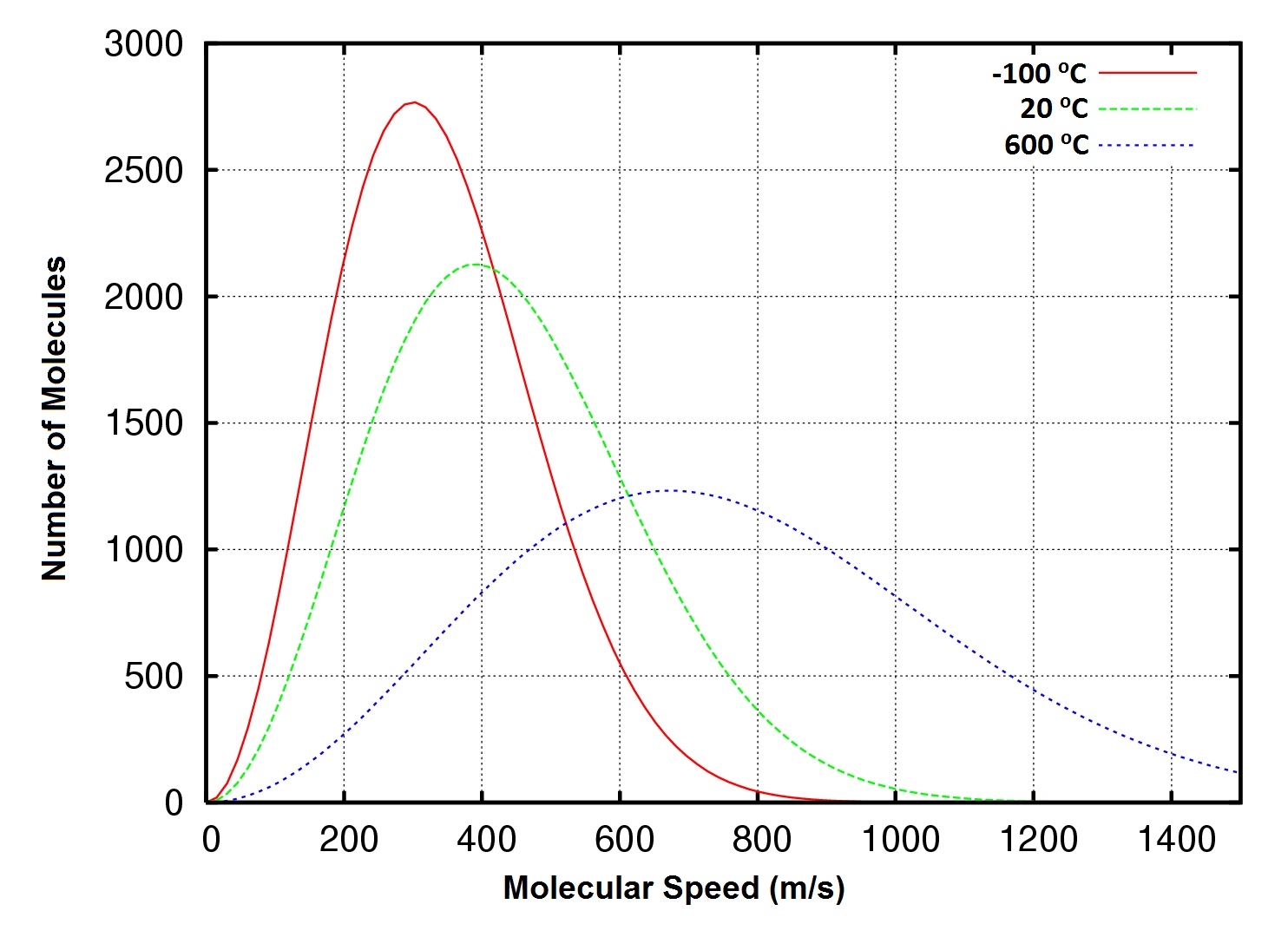
図6.＃分子速度の分布、-100、20、600℃の酸素ガス

図6.8 分子速度の分布、-100、20、600℃の酸素ガス

運動分子論によると、気体粒子の平均運動エネルギーは気体の絶対温度に比例します。 これは、kがボルツマン定数を表す次の式で表すことができます。 ボルツマン定数とは、気体定数Rをアボガドロ定数（NA）で割ったものです。

Overline{E_k} = ˶ˆ꒳ˆ˵ )

平均運動エネルギーは、絶対温度と分子速度の両方に関係しているので、上の式と前の式を組み合わせて実効速度を求めることができます。 \RMS速度 \m}を用いて \♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪ \♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪ \♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪

$sqrt{#overline{u^2}} = ˶ˆ꒳ˆ˵ ) これは、実効速度が温度と関係していることを示しています。 さらに、この式の分子と分母にアボガドロ定数(NA)をかけると、気体定数(R)とモル質量(M)を使った形になります。

$sqrt{#overline{u^2}}\ = sqrt{#frac{3RT}{M}}$

この式は、気体分子の実効速度が物質のモル質量にも関係していることを示しています。 同じ温度でモル質量の異なる2つの気体を比較すると、平均運動エネルギーが同じであるにもかかわらず、モル質量の小さい気体の方が実効速度が大きいことがわかります。

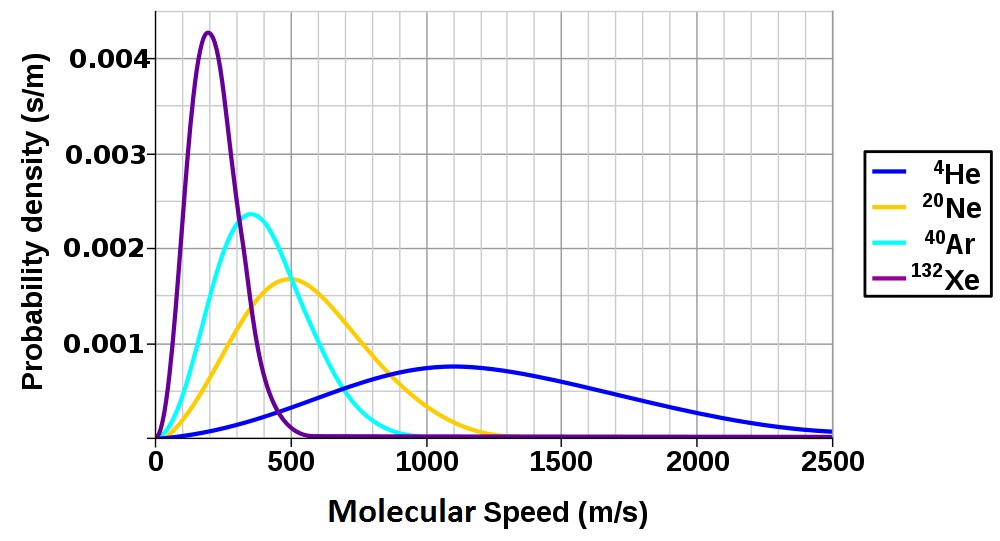
Figure 6.# Noble Gasesの分子速度分布

Figure 6.9 Molecular Speed Distribution of Noble Gases

Example 19
25℃における窒素分子の実効速度を計算してください。解答$sqrt{\overline{u^2}}=\sqrt{\frac{3RT}{M}}=\frac{3(8.3145\ J{K}^{-1}{ mol}^{-1})(298.15\ K)}{28.02\ x\{10}^{-3}\ kg{ mol}^{-1}}$$\sqrt{\overline{u^2}}=\sqrt{2.654\\ J\ {10}^{5}J\ {kg}^{-1}}$ 1J=1kg m2 s-2であることから、メートル毎秒に換算すると、\sqrt{overline{u^2}}=\sqrt{2.10}^{5}J\ {kg}^{-1}\ ¶frac{1kg\ m^2{s}^{-2}}{1J}}\ ¶sqrt{overline{u^2}= ¶sqrt{2.654\ {10}^{5}m^2{s}^{-2}} ¶textit{ = 515.2 m}}。

Applying the Kinetic Molecular Theory to the Gas Laws

気体の法則を作るために使われた実験の傾向を、運動論的分子理論を使って説明したり予測したりすることができます。

一定の温度で体積が減少した系の圧力はどうなるでしょうか。

この問題は2つの方法で取り組むことができます：

1.

理想気体の法則を並べ替えて圧力を解き、圧力の変化を見積もる

textit{PV = nRT}

textit{P = }\frac{nRT}{V}\textit{}

体積は式の分母に位置し、減少しています。

2.運動分子論が使えます。 温度が一定なので、平均運動エネルギーと実効速度も同じになります。 容器の体積が小さくなったので、気体の分子が衝突するまでの距離が短くなりました。

温度が上がり、体積が一定の場合、圧力はどうなるでしょうか。

また、この種の問題には2つのアプローチがあります。

理想気体の法則を並べ替えて圧力を解き、圧力の変化を見積もる

textit{p = }\frac{nRT}{V}\textit{}

分子には温度が入っており、温度と圧力には直接的な関係があります。

2.動力学的分子論が使えます。 温度が上昇すれば、平均運動エネルギーと実効速度も上昇するはずです。 これは、ガス分子がより頻繁に、より大きな力で容器の壁に衝突することを意味します。

Key Takeaways

  • 気体の物理的な挙動は、気体の運動分子理論によって説明されます。
  • 気体粒子が容器の壁に衝突する回数と衝突する力が、気体の圧力の大きさを決定します。
  • 温度は平均運動エネルギーに比例します。

練習問題

  1. 気体の運動分子論の考え方を述べなさい
  2. 40℃のCO2のrms速度を計算しなさい。
  3. 運動分子論を用いて、体積と温度が一定の気体のモル数の増加が圧力にどのように影響するかを説明してください。

回答

  1. 気体は常に運動している小さな物質の粒子から成り立っています。 気体の粒子は、お互いに、また容器の壁に常に衝突しています。 これらの衝突は弾性的であり、衝突によるエネルギーの正味の損失はありません。 気体粒子は大きな距離を隔てている。 気体粒子の大きさは、粒子間の距離や容器の容積に比べてわずかである。 気体の粒子間には相互作用的な力（引力や反発）はありません。 気体粒子の平均運動エネルギーは、気体の温度に依存します。
  2. 421 m/s
  3. 温度は変わらないので、平均運動エネルギーと実効速度は変わらないはずです。 気体のモル数が増えるということは、いつでも容器の壁に衝突できる気体の分子の数が増えるということです。 したがって、圧力は増加するはずです。

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です