決定論的有限オートマトン
決定論的有限オートマトン(DFA)は、5つの要素のタプルで記述されます。 (Q,Σ,δ,q0,F)(Q, ˶‾᷄ -̫ ‾᷅˵)(Q,Σ,δ,q0,F)です。
QQQ = 有限の状態の集合
ΣSigmaΣ = 有限の。
ΣSigmaΣ = 有限、空でない入力アルファベット
δdeltaδ = 一連の遷移関数
q0q_0q0 = 開始状態
FFF = 受諾状態の集合
ΣSigmaΣの各状態からの入力記号に対して、正確に1つの遷移関数が存在しなければならない。
DFAは次のような形式の図で表すことができます。 
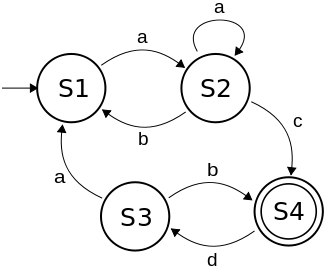
以下の有限状態機械で生成できない文字列は?
ここでは、ビデオゲームのキャラクターが行うことのできるいくつかの単純な動き、すなわち、立つ、走る、跳ぶ、を記述したDFA図を示します。 プレイヤーがこのキャラクターを操作するために使用できるボタンは「上」「A」、またはプレイヤーはボタンを押すことができません。

上記のビデオゲームのキャラクターの状態図を使って、プレイヤーがキャラクターを制御して、立つ→走る→ジャンプするまでの流れを説明してください。
Show Answer立っている状態では、プレイヤーは何も押さずに立ったままの状態を維持し、走っている状態に移行するためには「上」ボタンを押す必要があります。 走行状態では、”上 “ボタンを押すことでキャラクターを走らせ続けることができ、ジャンプ状態に移行するには “A “ボタンを押す必要があります。
以下の言語を認識するDFAの図を作成します。 1で終わるすべての文字列の言語。
Show Answer
非決定論的有限オートマトン
QQQ = 状態の有限集合
ΣSigmaΣ = 有限の。
ΣSigmaΣ = finite, non-empty input alphabet
δδδ = 一連の遷移関数
q0q_0q0 = 開始状態
FFF = 受諾状態の集合
DFAとは異なり、NDFAはΣSigmaΣのすべてのシンボルに対して遷移関数を持つ必要はなく、同じシンボルに対して同じ状態に複数の遷移関数が存在することもあります。 さらに、NDFAはϵ( ‘Θ’ )で示されるヌル遷移を使用することができます。 NULLトランジションを使用すると、シンボルを読まなくても、マシンがある状態から別の状態にジャンプすることができます。
NDFAが文字列xxxを受け入れるのは、その文字列と互換性のあるパスが存在し、そのパスがaccept状態で終わる場合です。
NDFAはこのような形の図で表すことができます。
 source
source
上のNDFAが認識する言語を記述してください。
Show Answer上記のNDFAは、”10 “で終わる文字列と “01 “で終わる文字列を認識します。
状態aaaがスタート状態で、そこから何個でも1と0を好きな順番で並べた文字列を作り、状態bbや状態eeに移行してもいいし、すぐに状態bbや状態eeに移行してもいい。 いずれにしても、NDFAは、状態ddまたは状態gggに到達した文字列しか受け付けません。 状態 ddd または状態 ggg に到達するためには、文字列は「01」(状態 ddd の場合)または「10」(状態 ggg の場合)で終わる必要があります。
例えば、以下の文字列はすべてこの NDFA で認識されます。
- 00000000010
- 10
- 01
- 1111101
以下の有限状態機械で生成できない文字列はどれか。

以下の言語を記述したNDFAの図を描いてください。
Show Answer
。

