![]()
ベルヌーイ分布は、![]()
![]() で示される2つの可能な結果を持つ離散分布です。
で示される2つの可能な結果を持つ離散分布です。![]() n=0と
n=0と![]()
![]()
![]()
![]()
![]() で発生する。pとなります。 ここで
で発生する。pとなります。 ここで![]() となります。 そのため、確率密度関数
となります。 そのため、確率密度関数
|
(1)
|
となります。
これは次のようにも書けます
|
(2)
|
対応する分布関数は
となります。 これに対応する分布関数は
|
(3)
|
ベルヌーイ分布はWolframLanguageではBernoulliDistributionとして実装されています。
一定の試行回数を一定の成功確率で行うことをベルヌーイ試行といいます。
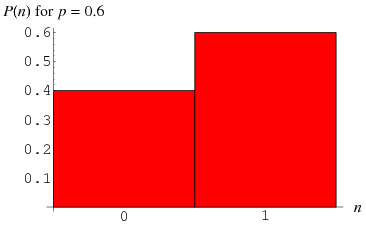
コイン投げの頭と尻尾の分布は![]() のベルヌーイ分布の例です。 ベルヌーイ分布は最も単純な離散的分布であり、より複雑な離散的分布の構成要素となります。 何らかの方法で縮小された独立したベルヌーイ試行のシーケンスに基づいて定義された多くの種類の変量の分布は、以下の表にまとめられています(Evans et al.2000, p.32)。
のベルヌーイ分布の例です。 ベルヌーイ分布は最も単純な離散的分布であり、より複雑な離散的分布の構成要素となります。 何らかの方法で縮小された独立したベルヌーイ試行のシーケンスに基づいて定義された多くの種類の変量の分布は、以下の表にまとめられています(Evans et al.2000, p.32)。
| 分布 | 定義 |
| 二項分布 | |
| 幾何学的分布 | 最初の成功の前の失敗の数 | 定義 |
| 負の二項分布 | |
特性関数は
|
(4)
|
そして、モーメントを発生させる関数は
となります。生成関数は
|
(5)
|
|||
|
(6)
|
|||
|
(7)
|
so
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
これは
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
と中心モーメント
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
平均、分散、歪度。となります。
|
(18)
|
|||
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
推定量を求めるには ![]()
![]()
![]()
![]()
![]() となります。 次のように与えられる推定量を仮定します
となります。 次のように与えられる推定量を仮定します
|
(22)
|
だから、観測されたものが得られる確率は ![]() 回の試行で成功する確率は、次のようになります
回の試行で成功する確率は、次のようになります
|
(23)
|
推定量![]() の期待値は、したがって次のように与えられます
の期待値は、したがって次のように与えられます
|
(24)
|
|||
|
(25)
|
|||
|
(26)
|
ソ ![]()
![]() の不偏推定量となります。
の不偏推定量となります。
平均偏差は次のように与えられます
|
(27)
|
となります。