Automi finiti deterministici
Un automa finito deterministico (DFA) è descritto da una tupla di cinque elementi: (Q,Σ,δ,q0,F)(Q, \Sigma, \delta, q_0, F)(Q,Σ,δ,q0,F).
QQQ = un insieme finito di stati
Σ\SigmaΣ = un alfabeto finito,
δ\deltaδ = una serie di funzioni di transizione
q0q_0q0 = lo stato iniziale
FFF = l’insieme degli stati accettanti
Ci deve essere esattamente una funzione di transizione per ogni simbolo di ingresso in Σ\SigmaΣ da ogni stato.
Le DFA possono essere rappresentate da diagrammi di questa forma: 
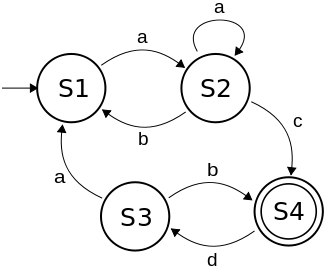
Quale stringa non può essere generata dalla macchina a stati finiti sottostante?
Ecco un diagramma DFA che descrive alcune semplici mosse che un personaggio di un videogioco può fare: stare in piedi, correre e saltare. I pulsanti che un giocatore può usare per controllare questo particolare personaggio sono “Su”, “A”, o il giocatore può non premere alcun pulsante.

Utilizzando il diagramma di stato del personaggio del videogioco di cui sopra, descrivi come un giocatore può controllare il suo personaggio per passare dallo stare in piedi al correre al saltare.
Show AnswerNello stato in piedi, il giocatore non può premere nulla e rimanere nello stato in piedi, poi, per passare allo stato di corsa, l’utente deve premere il pulsante “Su”. Nello stato di corsa, l’utente può continuare a far correre il suo personaggio premendo il pulsante “Su”, e poi, per passare allo stato di salto, l’utente deve premere “A.”
Disegna un diagramma per un DFA che riconosce il seguente linguaggio: Il linguaggio di tutte le stringhe che finiscono con un 1.
Mostra risposta
Automi finiti non deterministici
QQQ = un insieme finito di stati
Σ\SigmaΣ = un alfabeto finito,
δ\deltaδ = una serie di funzioni di transizione
q0q_0q0 = lo stato iniziale
FFF = l’insieme degli stati accettati
A differenza dei DFA, gli NDFA non sono tenuti ad avere funzioni di transizione per ogni simbolo in Σ\SigmaΣ, e ci possono essere più funzioni di transizione nello stesso stato per lo stesso simbolo. Inoltre, gli NDFA possono usare transizioni nulle, che sono indicate da ϵepsilonϵ. Le transizioni nulle permettono alla macchina di saltare da uno stato all’altro senza dover leggere un simbolo.
Un NDFA accetta una stringa xxx se esiste un percorso compatibile con quella stringa che termina in uno stato di accettazione.
Le NDFA possono essere rappresentate da diagrammi di questa forma:
 source
source
Descrivi il linguaggio che l’NDFA di cui sopra riconosce.
Mostra rispostaIl NDFA di cui sopra riconosce le stringhe che finiscono in “10” e quelle che finiscono in “01”.
Lo stato aaa è lo stato iniziale, e da lì, possiamo creare una stringa con quanti 1 e 0 in qualsiasi ordine, e poi passare allo stato bbb o allo stato eee, oppure possiamo passare immediatamente allo stato bbb o allo stato eee. In ogni caso, l’NDFA accetterà solo una stringa che raggiunge lo stato ddd o lo stato ggg. Per raggiungere lo stato ddd o lo stato ggg, la stringa deve finire con un “01” (per lo stato ddd) o un “10” (per lo stato ggg).
Per esempio, le seguenti stringhe sono tutte riconosciute da questo NDFA.
- 00000000010
- 10
- 01
- 1111101
Quale stringa non può essere generata dalla macchina a stati finiti sottostante?

Disegna un diagramma per il NDFA che descriva il seguente linguaggio: Il linguaggio di tutte le stringhe che finiscono con un 1.
Show Answer

