Distribuzione di Bernoulli

By admin on

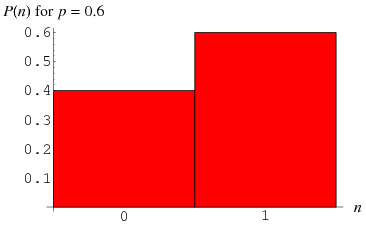
DOWNLOAD Mathematica NotebookBernoulliDistribution

La distribuzione di Bernoulli è una distribuzione discreta con due possibili risultati etichettati da n=0 e n=1 in cui n=1 (“successo”) avviene con probabilità p e n=0 (“fallimento”) si verifica con probabilità q=1-p, dove 0p1. Ha quindi funzione di densità di probabilità

P(n)={1-p per n=0; p per n=1,
(1)

che può anche essere scritto

P(n)=p^n(1-p)^(1-n).
(2)

La funzione di distribuzione corrispondente è

D(n)={1-p per n=0; 1 per n=1.
(3)

La distribuzione Bernoulli è implementata nel linguaggio Wolfram come BernoulliDistribution.

L’esecuzione di un numero fisso di prove con una probabilità fissa di successo per ogni prova è nota come una prova di Bernoulli.

La distribuzione di testa e croce nel lancio della moneta è un esempio di distribuzione di Bernoulli con p=q=1/2. La distribuzione di Bernoulli è la più semplice distribuzione discreta, ed è il blocco di costruzione per altre distribuzioni discrete più complicate. Le distribuzioni di un certo numero di tipi di variabili definite sulla base di sequenze di prove indipendenti di Bernoulli che vengono ridotte in qualche modo sono riassunte nella seguente tabella (Evans et al. 2000, p. 32).

distribuzione definizione
distribuzione binomiale numero di successi in n prove
distribuzione geometrica numero di fallimenti prima il primo successo
distribuzione binomiale negativa numero di fallimenti prima del xsimo successo

La funzione caratteristica è

phi(t)=1+p(e^(it)-1),
(4)

e la funzione generatrice di momentiè

M(t) = e^(tn)
(5)
= sum_(n=0)^(1)e^(tn)p^n(1-p)^(1-n)
(6)
= e^0(1-p)+e^tp,
(7)

così

M(t) = (1-p)+pe^t
(8)
M^'(t)'(t) = pe^t
(9)
M^('')(t)'')(t) = pe^t
(10)
M^((n))(t) = pe^t.
(11)

Questi danno momenti crudi

mu_1^'' = p
(12)
mu_2^'' = p
(13)
mu_n^'' = p.
(14)

e momenti centrali

mu_2 = p(1-p)
(15)
mu_3 = p(1-p)(1-2p)
(16)
mu_4 = p(1-p)(3p^2-3p+1).
(17)

Media, varianza, asimmetria,e l’eccesso di curtosi sono quindi

mu = p
(18)
sigma^2 = p(1-p)
(19)
gamma_1 = (1-2p)/(sqrt(p(1-p)))
(20)
gamma_2 = (6p^2-6p+1)/(p(1-p)).
(21)

Per trovare uno stimatore p^^ per la media di una popolazione di Bernoulli con media di popolazione p, Sia N la dimensione del campione e supponiamo che n successi siano ottenuti dalle N prove. Assumere uno stimatore dato da

p^^=n/N,
(22)

così che la probabilità di ottenere il n successi in N prove è quindi

(N; n)p^n(1-p)^(N-n).
(23)

Il valore di aspettativa dello stimatore p^^ è quindi dato da

p^^ = sum_(n=0)^(N)p(N; n)p^n(1-p)^(N-n)
(24)
= (1-p)^N(1/(1-p))^Np
(25)
= p,
(26)

così p^^ è effettivamente uno stimatore imparziale per la media della popolazione p.

La deviazione media è data da

MD=2p(1-p).
(27)

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *