Analisi dei fattori

DefinizioneModifica

Il modello cerca di spiegare un insieme di p osservazioni in ciascuno degli n individui con un insieme di k fattori comuni (F) dove ci sono meno fattori per unità che osservazioni per unità (k<p). Ogni individuo ha k dei propri fattori comuni, e questi sono collegati alle osservazioni tramite la matrice di caricamento dei fattori ( L ∈ R p × k {displaystyle L\in \mathbb {R} ^{p\times k}}

), per una singola osservazione, secondo x i , m – μ i = l i , 1 f 1 , m + ⋯ + l i , k f k , m + ϵ i , m {\displaystyle x_{i,m}-\mu _{i}=l_{i,1}f_{1,m}+\punti +l_{i,k}f_{k,m}+\epsilon _{i,m}}

dove ϵ i , m {displaystyle \epsilon _{i,m}

è il termine di errore stocastico non osservato con media zero e varianza finita, e μ i {displaystyle \mu _{i}}

è la media di osservazione per l’iesima osservazione.

In notazione matriciale

X – M = L F + ϵ {displaystyle X-\mathrm {M} =LF+\epsilon }

dove la matrice di osservazione X ∈ R p × n {displaystyle X\in \mathbb {R} ^{p\times n}}

, matrice fattore F ∈ R k × n {displaystyle F in \mathbb {R} ^{k\times n}}

, matrice dei termini di errore ϵ ∈ R p × n {displaystyle \epsilon \mathbb {R} ^{p\times n}

e matrice media M ∈ R p × n {displaystyle \mathrm {M} \in \mathbb {R} ^{p\times n}}

dove l’elemento i, m è semplicemente μ i {\displaystyle \mu _{i}

.

Inoltre imporremo le seguenti assunzioni su F {\displaystyle F}

:

1. F e ϵ {displaystyle \epsilon }
   

   sono indipendenti.

2. E ( F ) = 0 {displaystyle \mathrm {E} (F)=0}
   

   ; dove E è l’aspettativa

3. C o v ( F ) = I {\displaystyle \mathrm {Cov} (F)=I}
   

   dove Cov è la matrice di covarianza, per assicurarsi che i fattori non siano correlati, e I è la matrice di identità.

Supponiamo che C o v ( X – M ) = Σ {displaystyle \mathrm {Cov} (X-\mathrm {M} )=\Sigma }

. Allora Σ = C o v ( X – M ) = C o v ( L F + ϵ ) , {\displaystyle \Sigma =\mathrm {Cov} (X-\mathrm {M} )=\mathrm {Cov} (LF+\epsilon ),\,

e quindi, dalle condizioni imposte su F sopra,

Σ = L C o v ( F ) L T + C o v ( ϵ ) , {\displaystyle \Sigma =L\mathrm {Cov} (F)L^{T}+\mathrm {Cov} (\epsilon ),\,

o, impostando Ψ = C o v ( ϵ ) {displaystyle \Psi =\mathrm {Cov} (\epsilon )}

, Σ = L L T + Ψ .

Nota che per qualsiasi matrice ortogonale Q, se impostiamo L ′ = L Q {\displaystyle L^{prime }=LQ}

e F ′ = Q T F {displaystyle F^{\prime }=Q^{T}F}

, i criteri per essere fattori e i caricamenti dei fattori sono ancora validi. Quindi un insieme di fattori e di caricamenti dei fattori è unico solo fino a una trasformazione ortogonale.

EsempioModifica

Supponiamo che uno psicologo abbia l’ipotesi che ci siano due tipi di intelligenza, “intelligenza verbale” e “intelligenza matematica”, nessuna delle quali è direttamente osservata. Le prove dell’ipotesi sono ricercate nei punteggi degli esami di ciascuno dei 10 diversi campi accademici di 1000 studenti. Se ogni studente è scelto a caso da una grande popolazione, allora i 10 punteggi di ogni studente sono variabili casuali. L’ipotesi dello psicologo può dire che per ciascuno dei 10 campi accademici, il punteggio medio sul gruppo di tutti gli studenti che condividono una coppia di valori comuni per le “intelligenze” verbale e matematica è una costante per il loro livello di intelligenza verbale più un’altra costante per il loro livello di intelligenza matematica, cioè è una combinazione lineare di questi due “fattori”. I numeri per un particolare soggetto, per i quali si moltiplicano i due tipi di intelligenza per ottenere il punteggio atteso, sono posti dall’ipotesi per essere gli stessi per tutte le coppie di livelli di intelligenza, e sono chiamati “carico dei fattori” per questo soggetto. Per esempio, l’ipotesi può essere che l’attitudine media prevista dello studente nel campo dell’astronomia sia

{10 × l’intelligenza verbale dello studente} + {6 × l’intelligenza matematica dello studente}.

I numeri 10 e 6 sono i carichi di fattore associati all’astronomia. Altre materie accademiche possono avere carichi di fattore diversi.

Due studenti che si presume abbiano gli stessi gradi di intelligenza verbale e matematica possono avere diverse attitudini misurate in astronomia perché le attitudini individuali differiscono dalle attitudini medie (previste sopra) e a causa dell’errore di misurazione stesso. Tali differenze costituiscono ciò che viene chiamato collettivamente “errore” – un termine statistico che significa la quantità di cui un individuo, come misurato, differisce da ciò che è medio per o predetto dai suoi livelli di intelligenza (vedi errori e residui in statistica).

I dati osservabili che vanno nell’analisi dei fattori sarebbero 10 punteggi di ciascuno dei 1000 studenti, un totale di 10.000 numeri. I caricamenti dei fattori e i livelli dei due tipi di intelligenza di ogni studente devono essere dedotti dai dati.

Modello matematico dello stesso esempioModifica

Nel seguito, le matrici saranno indicate da variabili indicizzate. Gli indici “soggetto” saranno indicati con le lettere a {\displaystyle a}

, b {\displaystyle b}

e c {displaystyle c}

, con valori che vanno da 1 {displaystyle 1}

a p {\displaystyle p}

che è uguale a 10 {\displaystyle 10}

nell’esempio precedente. Gli indici “fattore” saranno indicati con le lettere p {\displaystyle p}

, q {\displaystyle q}

e r {\displaystyle r}

, con valori che vanno da 1 {\displaystyle 1}

a k {displaystyle k}

che è uguale a 2 {\displaystyle 2}

nell’esempio precedente. Gli indici “istanza” o “campione” saranno indicati con le lettere i {\displaystyle i}

, j {\displaystyle j}

e k {\displaystyle k}

, con valori che vanno da 1 {displaystyle 1}

a N {\displaystyle N}

. Nell’esempio precedente, se un campione di N = 1000 {\displaystyle N=1000}

gli studenti hanno partecipato al p = 10 {displaystyle p=10}

esami, i {displaystyle i}

il punteggio del terzo studente per l’a {displaystyle a}

terzo esame è dato da x a i {displaystyle x_{ai}}

. Lo scopo dell’analisi dei fattori è quello di caratterizzare le correlazioni tra le variabili x a {\displaystyle x_{a}}

di cui la x a i {\displaystyle x_{ai}

sono una particolare istanza, o insieme di osservazioni. Affinché le variabili siano su un piano di parità, sono normalizzate in punteggi standard z {\displaystyle z}

: z a i = x a i – μ a σ a {\displaystyle z_{ai}={\frac {x_{ai}-\mu _{a}}{\sigma _{a}}}}

dove la media del campione è:

μ a = 1 N ∑ i x a i {\displaystyle \mu _{a}={tfrac {1}{N}}}sum _{i}x_{ai}

e la varianza del campione è data da:

σ a 2 = 1 N – 1 ∑ i ( x a i – μ a ) 2 {displaystyle \sigma _{a}^{2}={tfrac {1}{N-1}}}somma _{i}(x_{ai}-\mu _{a})^{2}}

Il modello di analisi dei fattori per questo particolare campione è quindi:

z 1 , i = ℓ 1 , 1 F 1 , i + ℓ 1 , 2 F 2 , i + ε 1 , i ⋮ ⋮ ⋮ ⋮ z 10 , i = ℓ 10 , 1 F 1 , i + ℓ 10 , 2 F 2 , i + ε 10 , i {\displaystyle {begin{matrix}z_{1,i}&&&&&iv id=”1,2}F_{2,i}&&\varepsilon _{1,i}\vdots &&\vdots &&\vdots &&\vdots \\\z_{10,i}&&{div>ell _{10,1} F_{1,i}&&ell _{10,2}F_{2,i}&&\varepsilon _{10,i}\end{matrix}}}

o, più brevemente:

z a i = ∑ p ℓ a p F p i + ε a i {\displaystyle z_{ai}=somma _{p}\ell _{ap}F_{pi}+\varepsilon _{ai}

dove

• F 1 i {\displaystyle F_{1i}}
  

  è la i {displaystyle i}

  

  l'”intelligenza verbale” dello studente,

• F 2 i {\displaystyle F_{2i}
  

  è l’i {displaystyle i}

  

  l'”intelligenza matematica” dello studente,

• ℓ a p {displaystyle \ell _{ap}
  

  sono i carichi dei fattori per il soggetto a {\displaystyle a}

  

  , per p = 1 , 2 {\displaystyle p=1,2}

  

  .

In notazione matriciale, abbiamo

Z = L F + ε {displaystyle Z=LF+\varepsilon }

Osserva che raddoppiando la scala su cui “l’intelligenza verbale” – la prima componente in ogni colonna di F {displaystyle F}

– viene misurata, e contemporaneamente dimezzando i caricamenti dei fattori per l’intelligenza verbale non c’è differenza nel modello. Quindi, non si perde nessuna generalità assumendo che la deviazione standard dei fattori per l’intelligenza verbale sia 1 {\displaystyle 1}

. Lo stesso vale per l’intelligenza matematica. Inoltre, per ragioni simili, non si perde generalità assumendo che i due fattori non siano correlati tra loro. In altre parole: ∑ i F p i F q i = δ p q {displaystyle \sum _{i}F_{pi}F_{qi}=\delta _{pq}}

dove δ p q {displaystyle \delta _{pq}}

è il delta di Kronecker ( 0 {displaystyle 0}

quando p ≠ q {displaystyle p\neq q}

e 1 {\displaystyle 1}

quando p = q {\displaystyle p=q}

).Si suppone che gli errori siano indipendenti dai fattori: ∑ i F p i ε a i = 0 {displaystyle \sum _{i}F_{pi}\varepsilon _{ai}=0}

Nota che, poiché ogni rotazione di una soluzione è anche una soluzione, questo rende difficile l’interpretazione dei fattori. Vedi gli svantaggi qui sotto. In questo particolare esempio, se non sappiamo in anticipo che i due tipi di intelligenza non sono correlati, allora non possiamo interpretare i due fattori come i due diversi tipi di intelligenza. Anche se non sono correlati, non possiamo dire quale fattore corrisponde all’intelligenza verbale e quale all’intelligenza matematica senza un argomento esterno.

I valori dei caricamenti L {displaystyle L}

, le medie μ {displaystyle \mu }

, e le varianze degli “errori” ε {displaystyle \varepsilon }

devono essere stimati dati i dati osservati X {displaystyle X}

e F {displaystyle F}

(l’ipotesi sui livelli dei fattori è fissa per un dato F {\displaystyle F}

). Il “teorema fondamentale” può essere derivato dalle condizioni di cui sopra: ∑ i z a i z b i = ∑ j ℓ a j ℓ b j + ∑ i ε a i ε b i {displaystyle \sum _{i}z_{ai}z_{bi}=sum _{j}ell _{aj}\ell _{bj}+sum _{i}varepsilon _{ai}{bi}

Il termine a sinistra è il ( a , b ) {\displaystyle (a,b)}

-termine della matrice di correlazione (a p × p {\displaystyle p\times p}

matrice derivata come prodotto delle p × N {displaystyle p\times N}

matrice di osservazioni standardizzate con la sua trasposizione) dei dati osservati, e la sua p {displaystyle p}

elementi diagonali saranno 1 {displaystyle 1}

s. Il secondo termine a destra sarà una matrice diagonale con termini inferiori all’unità. Il primo termine a destra è la “matrice di correlazione ridotta” e sarà uguale alla matrice di correlazione tranne i suoi valori diagonali che saranno inferiori all’unità. Questi elementi diagonali della matrice di correlazione ridotta sono chiamati “comunanze” (che rappresentano la frazione della varianza nella variabile osservata che è rappresentata dai fattori): h a 2 = 1 – ψ a = ∑ j ℓ a j ℓ a j {displaystyle h_{a}^{2}=1-\psi _{a}=somma _{j}ell _{aj}ell _{aj}}

I dati campione z a i {\displaystyle z_{ai}}

non obbediranno esattamente all’equazione fondamentale data sopra a causa di errori di campionamento, inadeguatezza del modello, ecc. L’obiettivo di qualsiasi analisi del modello di cui sopra è quello di trovare i fattori F p i {\displaystyle F_{pi}

e i caricamenti ℓ a p {\displaystyle \ell _{ap}}

che, in un certo senso, danno un “best fit” ai dati. Nell’analisi dei fattori, il miglior adattamento è definito come il minimo dell’errore quadratico medio nei residui fuori diagonale della matrice di correlazione: ε 2 = ∑ a ≠ b 2 {\displaystyle \varepsilon ^{2}=\somma _{a\neq b}\left^{2}

Questo equivale a minimizzare le componenti fuori-diagonale della covarianza degli errori che, nelle equazioni del modello hanno valori attesi pari a zero. Questo deve essere contrastato con l’analisi delle componenti principali che cerca di minimizzare l’errore quadratico medio di tutti i residui. Prima dell’avvento dei computer ad alta velocità, è stato dedicato uno sforzo considerevole per trovare soluzioni approssimative al problema, in particolare per stimare le comunanze con altri mezzi, che poi semplificano notevolmente il problema producendo una matrice di correlazione ridotta nota. Questa è stata poi utilizzata per stimare i fattori e le cariche. Con l’avvento dei computer ad alta velocità, il problema di minimizzazione può essere risolto iterativamente con velocità adeguata, e le comunanze sono calcolate nel processo, piuttosto che essere necessarie in anticipo. L’algoritmo MinRes è particolarmente adatto a questo problema, ma non è l’unico mezzo iterativo per trovare una soluzione.

Se i fattori della soluzione possono essere correlati (come nella rotazione ‘oblimin’, per esempio), allora il modello matematico corrispondente usa coordinate oblique piuttosto che coordinate ortogonali.

Interpretazione geometricaModifica

Interpretazione geometrica dei parametri dell’Analisi Fattoriale per 3 rispondenti alla domanda “a”. La “risposta” è rappresentata dal vettore unitario z a {displaystyle \mathbf {z} _{a}}

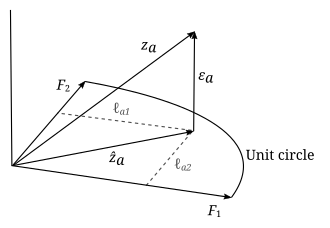
, che viene proiettato su un piano definito da due vettori ortonormali F 1 {displaystyle \mathbf {F} _{1}}

e F 2 {displaystyle \mathbf {F} _{2}}

. Il vettore di proiezione è z ^ a {displaystyle {\hat {mathbf {z} }}_{a}}

è perpendicolare al piano, così che z a = z ^ a + ε a {displaystyle \mathbf {z} _{a}={hat {mathbf {z} {{a}+{boldsymbol {{varepsilon}_{a}

. Il vettore di proiezione z ^ a {displaystyle {mathbf {z} }}_{a}}

. Il quadrato della lunghezza del vettore di proiezione è la comunanza: | z ^ a | 2 = h a 2 {\displaystyle ||{{{mathhat {\mathbf {z} }}_{a}||^{2}=h_{a}^{2}}

. Se un altro vettore di dati z b {displaystyle \mathbf {z} _{b}}

sono stati tracciati, il coseno dell’angolo tra z a {displaystyle \mathbf {z} _{a}}

e z b {displaystyle \mathbf {z} _{b}}

: il ( a , b ) {\displaystyle (a,b)}

-entrata nella matrice di correlazione. (Adattato da Harman Fig. 4.3)

I parametri e le variabili dell’analisi dei fattori possono essere interpretati geometricamente. I dati ( z a i {\displaystyle z_{ai}}

), i fattori ( F p i {\displaystyle F_{pi}}

) e gli errori ( ε a i {\displaystyle \varepsilon _{ai}}

) possono essere visti come vettori in un N {\displaystyle N}

-dimensionale spazio euclideo (spazio campione), rappresentato come z a {displaystyle \mathbf {z} _{a}}

, F j {displaystyle \mathbf {F} _{j}}

rispettivamente. Poiché i dati sono standardizzati, i vettori di dati sono di lunghezza unitaria ( | | z a | | = 1 {\displaystyle ||mathbf {z} _{a}||=1}

). I vettori fattoriali definiscono un k {displaystyle k}

-dimensionale sottospazio lineare (cioè un iperpiano) in questo spazio, sul quale i vettori dati sono proiettati ortogonalmente. Questo segue dall’equazione del modello z a = ∑ j ℓ a j F j + ε a {\displaystyle \mathbf {z} _{a}=somma _{j}ell _{aj}mathbf {\i} _{j}+{boldsymbol {{varepsilon}_{a}}

e l’indipendenza dei fattori e degli errori: F j ⋅ ε a = 0 {displaystyle \mathbf {F} _{j}\cdot {{j} {{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}{j}=0}

. Nell’esempio precedente, l’iperpiano è solo un piano bidimensionale definito dai due vettori fattore. La proiezione dei vettori dati sull’iperpiano è data da z ^ a = ∑ j ℓ a j F j {\displaystyle {\hat {mathbf {z} a = ∑ j ℓ a ∑ a ∑ a ∑ a ∑ a ∑ a ∑ a ∑ a ∑ a ∑ a ∑ a _{j}}

e gli errori sono vettori da quel punto proiettato al punto dei dati e sono perpendicolari all’iperpiano. L’obiettivo dell’analisi dei fattori è quello di trovare un iperpiano che è un “best fit” per i dati in un certo senso, quindi non importa come i vettori dei fattori che definiscono questo iperpiano sono scelti, purché siano indipendenti e giacciano nell’iperpiano. Siamo liberi di specificarli sia ortogonali che normali ( F j ⋅ F q = δ p q {\displaystyle \mathbf {F} F j = δ p q = δ p q = δ p q = δ p q = δ p q F q = δ p q}}

) senza perdita di generalità. Dopo aver trovato un adeguato insieme di fattori, essi possono anche essere arbitrariamente ruotati all’interno dell’iperpiano, in modo che qualsiasi rotazione dei vettori dei fattori definirà lo stesso iperpiano, e sarà anche una soluzione. Di conseguenza, nell’esempio precedente, in cui l’iperpiano di adattamento è bidimensionale, se non sappiamo in anticipo che i due tipi di intelligenza non sono correlati, allora non possiamo interpretare i due fattori come i due diversi tipi di intelligenza. Anche se non sono correlati, non possiamo dire quale fattore corrisponde all’intelligenza verbale e quale all’intelligenza matematica, o se i fattori sono combinazioni lineari di entrambi, senza un argomento esterno.

I vettori dati z a {displaystyle \mathbf {z} _{a}}

hanno lunghezza unitaria. Le voci della matrice di correlazione per i dati sono date da r a b = z a ⋅ z b {\displaystyle r_{ab}=\mathbf {z} _{a} {\a6}cdot \mathbf {z} _{b}}

. La matrice di correlazione può essere interpretata geometricamente come il coseno dell’angolo tra i due vettori dati z a {displaystyle \mathbf {z} _{a}}

e z b {displaystyle \mathbf {z} _{b}}

. Gli elementi diagonali saranno chiaramente 1 {displaystyle 1}

s e gli elementi fuori diagonale avranno valori assoluti minori o uguali all’unità. La “matrice di correlazione ridotta” è definita come r ^ a b = z ^ a ⋅ z ^ b {displaystyle {\hat {r}}_{ab}={hat {mathbf {z} {{a}}cdot {{mathbf {mathbf {z} }}_{b}}

.

L’obiettivo dell’analisi dei fattori è di scegliere l’iperpiano di adattamento in modo tale che la matrice di correlazione ridotta riproduca il più possibile la matrice di correlazione, ad eccezione degli elementi diagonali della matrice di correlazione che sono noti per avere valore unitario. In altre parole, l’obiettivo è quello di riprodurre il più accuratamente possibile le correlazioni incrociate nei dati. In particolare, per l’iperpiano di adattamento, l’errore quadratico medio nelle componenti fuori diagonale

ε 2 = ∑ a ≠ b ( r a b – r ^ a b ) 2 {\displaystyle \varepsilon ^{2}=somma _{a\neq b}\sinistra(r_{ab}-{hat {r}}_{ab}\ destra)^{2}}

deve essere minimizzato, e questo si ottiene minimizzandolo rispetto ad un insieme di fattori vettori ortonormali. Si può vedere che

r a b – r ^ a b = ε a ⋅ ε b {displaystyle r_{ab}-{hat {r}}_{ab}={{boldsymbol {{varepsilon }}_{a}\cdot {\boldsymbol {{varepsilon }}{b}

Il termine a destra è solo la covarianza degli errori. Nel modello, la covarianza degli errori è dichiarata essere una matrice diagonale e quindi il problema di minimizzazione di cui sopra produrrà in effetti un “best fit” al modello: Si otterrà una stima campionaria della covarianza degli errori che ha le sue componenti fuori diagonale minimizzate nel senso del quadrato medio. Si può vedere che poiché la z ^ a {displaystyle {hat {z}}_{a}}

sono proiezioni ortogonali dei vettori dati, la loro lunghezza sarà minore o uguale alla lunghezza del vettore dati proiettato, che è l’unità. I quadrati di queste lunghezze sono solo gli elementi diagonali della matrice di correlazione ridotta. Questi elementi diagonali della matrice di correlazione ridotta sono noti come “comunanze”: h a 2 = | z ^ a | 2 = ∑ j ℓ a j 2 {\displaystyle {h_{a}}^{2}=||{hat {\mathbf {z} {\an8}{a}}||^{2}=somma _{j}{ell _{aj}^{2}}