L’efficienza di un algoritmo dipende dalla quantità di tempo, memoria e altre risorse richieste per eseguire l’algoritmo. L’efficienza viene misurata con l’aiuto di notazioni asintotiche.
Un algoritmo può non avere le stesse prestazioni per diversi tipi di input. Con l’aumento della dimensione dell’input, la performance cambierà.
Lo studio del cambiamento della performance dell’algoritmo con il cambiamento dell’ordine della dimensione dell’input è definito come analisi asintotica.
Notazioni asintotiche
Le notazioni asintotiche sono le notazioni matematiche usate per descrivere il tempo di esecuzione di un algoritmo quando l’input tende verso un particolare valore o un valore limite.
Ad esempio: In bubble sort, quando l’array di input è già ordinato, il tempo impiegato dall’algoritmo è lineare, cioè il caso migliore.
Ma, quando l’array di input è in ordine inverso, l’algoritmo impiega il tempo massimo (quadratico) per ordinare gli elementi, cioè il caso peggiore.
Quando l’array di input non è né ordinato né in ordine inverso, allora richiede tempo medio. Queste durate sono indicate usando notazioni asintotiche.
Ci sono principalmente tre notazioni asintotiche:
- notazione Big-O
- notazione Omega
- notazione Theta
Notazione Big-O (O-notazione)
La notazione Big-O rappresenta il limite superiore del tempo di esecuzione di un algoritmo. Quindi, dà la complessità del caso peggiore di un algoritmo.
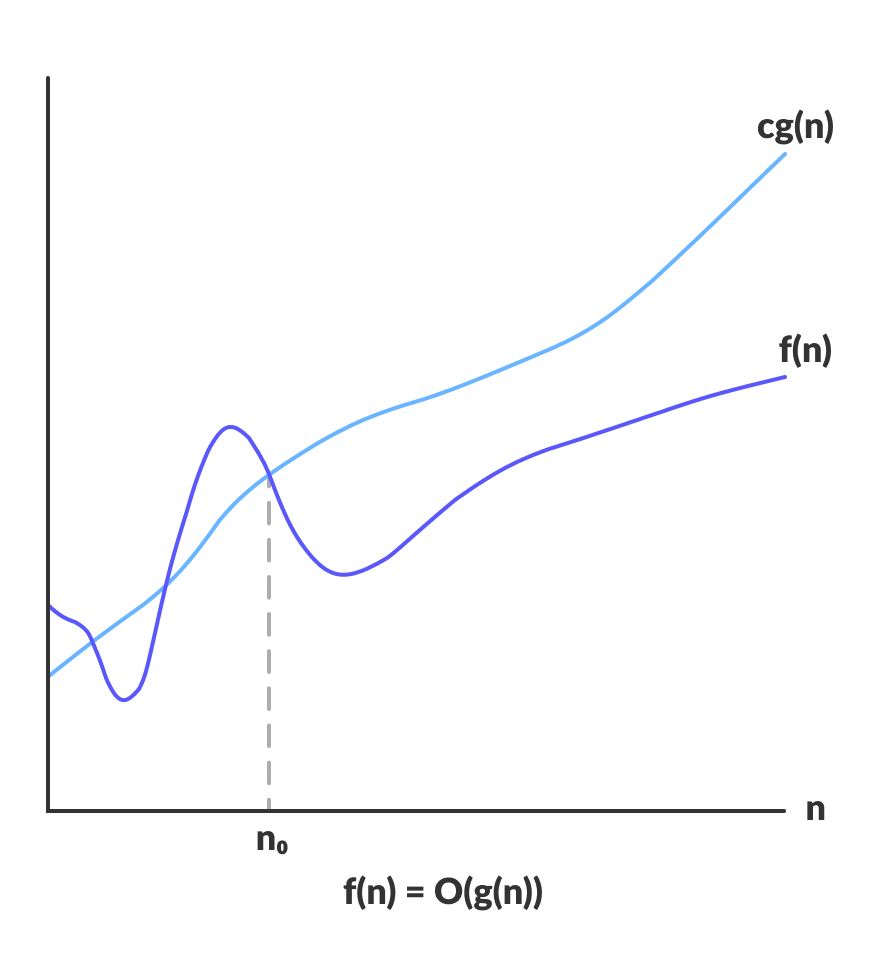
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
L’espressione precedente può essere descritta come una funzione f(n) appartiene all’insieme O(g(n)) se esiste una costante positiva c tale che si trova tra 0 e cg(n), per n sufficientemente grandi.
Per qualsiasi valore di n, il tempo di esecuzione di un algoritmo non supera quello fornito da O(g(n)).
Poiché fornisce il tempo di esecuzione nel caso peggiore di un algoritmo, è ampiamente utilizzato per analizzare un algoritmo in quanto siamo sempre interessati allo scenario peggiore.
Notazione Omega (Ω-notazione)
La notazione Omega rappresenta il limite inferiore del tempo di esecuzione di un algoritmo. Quindi, fornisce la complessità del caso migliore di un algoritmo.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
L’espressione precedente può essere descritta come una funzione f(n) appartiene all’insieme Ω(g(n)) se esiste una costante positiva c tale che si trova al di sopra cg(n), per n sufficientemente grande.
Per qualsiasi valore di n, il tempo minimo richiesto dall’algoritmo è dato da Omega Ω(g(n)).
Notazione Theta (Θ-notazione)
La notazione Theta racchiude la funzione da sopra e da sotto. Poiché rappresenta il limite superiore e inferiore del tempo di esecuzione di un algoritmo, è usata per analizzare la complessità del caso medio di un algoritmo.
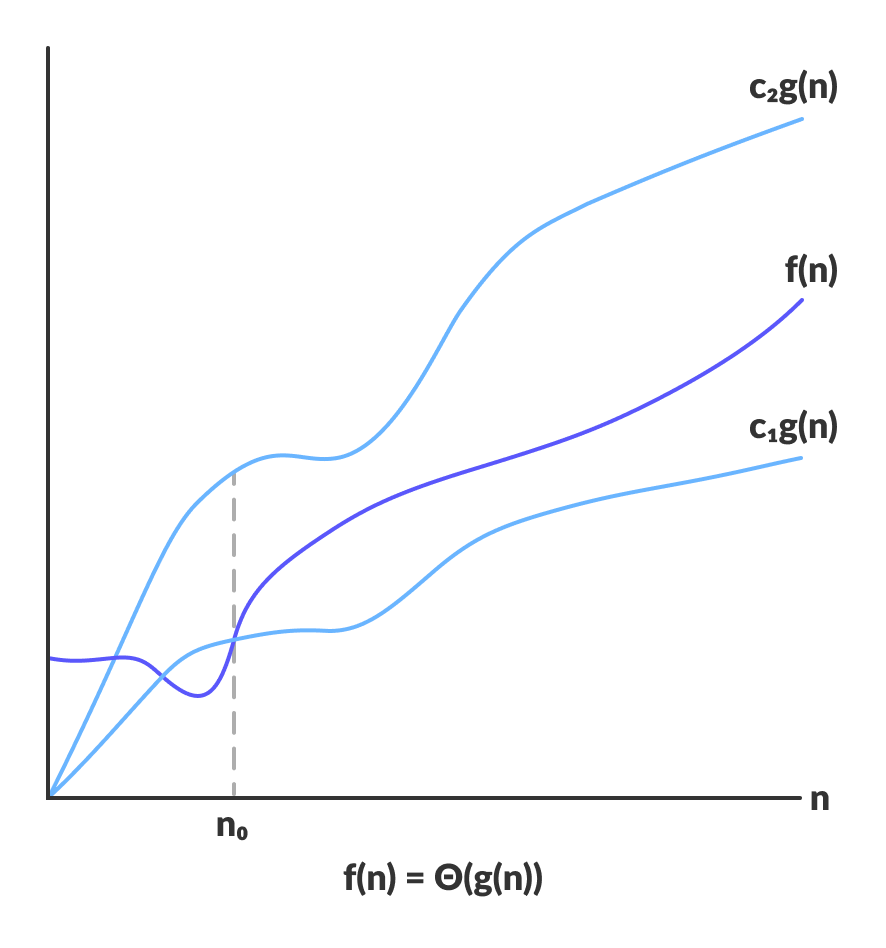
Per una funzione g(n)Θ(g(n)) è data dalla relazione:
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
L’espressione precedente può essere descritta come una funzione f(n) appartiene all’insieme Θ(g(n)) se esistono costanti positive c1 e c2 tali da poter essere inserita tra c1g(n) e c2g(n), per n sufficientemente grande.
Se una funzione f(n) si trova ovunque tra c1g(n) e c2g(n) per tutti n ≥ n0, allora f(n) si dice che è asintoticamente stretto.