
Sarò onesto. Ho fatto dei calcoli seri per più anni di quanto vorrei ammettere. A volte, in fisica, devi solo integrare le cose. È quello che succede.
Tuttavia, quando stavo aiutando mio figlio con il suo corso di calcolo ho iniziato a realizzare – che diavolo sta succedendo con l’integrazione? Mi sembra di avere una comprensione molto solida delle derivate – ma l’integrazione ha delle cose strane.
Beh, non riuscirai mai a capire le cose finché non le scomponi nei loro pezzi fondamentali. Quindi, questo è quello che farò. Troverò l’area sotto una curva in tre modi diversi.
Area usando la notazione di somma
Questa è la più facile da capire, ma la più difficile da calcolare. Oh, aspetta! Perché stiamo trovando l’area sotto una curva? OK, aspetta – il mio esempio alla fine dovrebbe aiutare.
Quindi, l’idea di base è di dividere un’area in N rettangoli (dove N è solo un numero). Posso poi trovare l’area di ogni rettangolo e sommarli per ottenere l’area totale. Più pezzi la divido, migliore sarà la risposta – quindi scriverò un’espressione per quest’area e prenderò il limite man mano che il numero di pezzi va all’infinito.

L’area sarebbe quindi calcolata come:
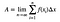
C’è un sacco di roba dopo questo – e diventa un po’ noioso. Tuttavia, si DEVE passare attraverso questo per comprendere appieno il tutto. Qui c’è un video in cui vi guido attraverso di esso.
Se usate una funzione:
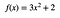
L’area da x = 1 a x =2 è 9 (qualunque siano le unità – non sono un matematico, quindi mi dà fastidio tralasciare le unità).
Area usando le antiderivate
C’è un trucco. È un trucco fantastico. Si può scrivere l’area sotto una curva come un integrale definito (dove l’integrale è una somma infinita di pezzi infinitamente piccoli – proprio come la notazione di somma).
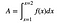
Ora le cose folli. CRAZY. Si scopre che l’area è l’antiderivata di f(x). Se vi fermate un attimo, vedrete che è pazzesco. Follemente selvaggio. Se la derivata ti dice qualcosa sulla pendenza di una curva, l’opposto della derivata ti dice l’area sotto la curva?
Sì. È il teorema fondamentale del calcolo. Ecco la mia spiegazione (sì, ci saranno un sacco di video in questo post e siete OBBLIGATI a guardarli tutti.
In realtà, c’è un’altra cosa importante qui. L’integrale definito da x = 1 a x =2 è la differenza della funzione area A(2) e A(1). Non andrò nei dettagli per questo perché la mia mente è ancora sconvolta per la cosa dell’antiderivata.
Ma qui c’è l’area sotto la STESSA funzione ma con integrazione.
Sì. Si ottiene lo stesso risultato finale. Area = 9 polli² (ho aggiunto le unità di area).
Area usando i calcoli numerici
Ora arriviamo alle cose divertenti. E se trovassi l’area sotto una curva sommando l’area di un mucchio di rettangoli? Oh, aspetta… l’ho già fatto nel primo metodo. Ma che ne dite di questo – non faccio un numero infinito di rettangoli, faccio solo un gran numero di rettangoli? Questo è esattamente ciò che riguarda un calcolo numerico.
Ovviamente, se rompo un’area in 100 pezzi dovrò fare 100 serie di calcoli di aree. Qualcuno vuole davvero farlo? No – nessuno pensa che sarebbe divertente. Ma sapete a chi non interessa? I computer (computer elettronici).
Sì, possiamo far fare a un computer questa serie di calcoli. Dobbiamo solo dargli delle istruzioni e poi andrà a fare il suo lavoro. Sarà fantastico. Ecco la ricetta di base che userà.
- Decidete in quanti pezzi volete spezzare la curva. Che ne dite di 100? Con questo e il valore x iniziale e finale, puoi calcolare la larghezza di ogni rettangolo (Δx).
- Imposta l’area a zero (chickens²). Continueremo ad aggiungere a questo valore, ma deve iniziare da qualche parte.
- Iniziare con il valore x iniziale (nell’esempio che ho usato – che è x = 1).
- Calcolare l’altezza del rettangolo. Questo sarebbe f(x) al valore corrente di x.
- Trova l’area di questo rettangolo e aggiungila all’area totale.
- Spostare sul prossimo valore di x e ripetere fino ad arrivare alla x finale.
Questo è così semplice che anche un computer potrebbe farlo. OK, mi sto solo divertendo. Alcuni dei miei migliori amici sono computer.
Qui c’è il codice per questo calcolo in python (qui c’è un link al codice effettivo).
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
Con N = 100, ottengo un’area di 8,95505 – che NON è esattamente 9 polli², ma è abbastanza dannatamente vicino. Abbastanza vicino per la maggior parte dei calcoli dei polli quadrati.
Solo alcuni commenti veloci su questo codice.
- Ho pensato che sarebbe stato divertente rendere la funzione una vera funzione python (questa è la parte
def f(t):. - Calcolo prima l’area del piccolo rettangolo (dA) e poi lo aggiungo all’area totale.
- Questo metodo ha effettivamente dei rettangoli allineati con la funzione sul lato sinistro della parte superiore del rettangolo. Si potrebbe fare anche con il lato destro.
- Ho anche fatto un video per questo. Ma non sei obbligato a guardarlo – per lo più l’ho già spiegato qui.
E se non hai una funzione matematica?
Ti metto nella seguente situazione. Sei in una macchina che sta guidando e puoi vedere SOLO il tachimetro. Scrivete il valore della velocità ogni secondo (perché siete super veloci a prendere appunti). L’auto alla fine si ferma e hai bisogno di scoprire quanto hai viaggiato.
Qui c’è qualcosa di simile (usando un carrello Vernier con un sensore di movimento – ma hai l’idea che questo è lo stesso di un’auto reale).

OK – attenzione, Sto per barare qui. Il binario Vernier raccoglie i dati di posizione in base a queste linee sul binario. Dai dati di posizione, calcola la velocità. Quindi, ho già la posizione del carrello – ma facciamo finta che dia solo la velocità in funzione del tempo. Forse sarebbe qualcosa di simile a questo.

Vedi. Quella non è una funzione – è una stazione spaziale. No, aspetta – quello è da Star Wars. Ma comunque, non è una funzione matematica. Sono solo dati. Non puoi trovare l’antiderivata dei dati (beh, non usando le normali regole e cose del genere). Ma aspettate! L’integrazione numerica funziona benissimo.
Ovviamente, c’è qualcos’altro di importante qui. È l’idea che l’area sotto questa curva rappresenti qualcosa di reale. Immaginate di avere un’auto che si muove con una velocità costante per un certo periodo di tempo. Potreste calcolare lo spostamento abbastanza facilmente:
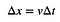
Se avete un grafico di velocità vs. tempo, questa velocità costante apparirebbe come un rettangolo. Sì, l’area di quel rettangolo sarebbe v*Δt. Se NON è una velocità costante, l’area sotto il grafico velocità-tempo sarebbe ancora lo spostamento.
OK, un ultimo video. Ecco la mia spiegazione del codice per risolvere questo problema di spostamento.
Assicurati di guardare tutti i video.