3: La forza di Coriolis

La forza di Coriolis è un elemento centrale della dinamica dei flussi oceanici e atmosferici. Una derivazione rigorosa usando il calcolo vettoriale è data in molti libri di testo sulla meccanica classica, ma tali derivazioni spesso non sono il modo più efficace per ottenere una comprensione concettuale. Pertanto, qui forniremo una spiegazione qualitativa più intuitiva. In tutto questo capitolo sui flussi geofisici, abbiamo parlato molto della seconda legge di Newton, ma la chiave per capire la forza di Coriolis è piuttosto la prima legge di Newton: un oggetto in movimento rimane in movimento con la stessa velocità e nella stessa direzione a meno che non sia agito da una forza sbilanciata. La Terra e tutto ciò che si trova su di essa è in costante movimento, poiché la Terra ruota attorno al suo asse. Inoltre, la direzione di tutto questo movimento cambia costantemente: mentre stai scrivendo alla tua scrivania alle 2 del pomeriggio, ti stai muovendo nella direzione esattamente opposta rispetto a quando eri sdraiato nel tuo letto alle 2 del mattino. Questi cambiamenti forzati nella direzione del movimento di oggetti che tendono a continuare a muoversi nella stessa direzione è ciò che dà origine alle cosiddette pseudo-forze (che in realtà sono molto reali, se vi capita di vivere su un pianeta rotante come la Terra).

La pseudo-forza che è più facile da capire concettualmente è la forza centrifuga, raffigurata qui sotto.

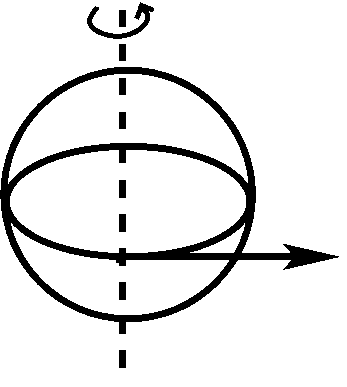
In sostanza, gli oggetti tendono ad essere buttati fuori da un corpo rotante, perché gli oggetti continuano a muoversi in linea retta (come indicato dalla freccia), mentre la superficie del corpo rotante non si muove in linea retta (come indicato dal cerchio). Fortunatamente, non dobbiamo preoccuparci di essere buttati fuori dalla Terra, perché la forza gravitazionale che mantiene i nostri piedi sulla terra è circa 300 volte più forte della forza centrifuga. La forza centrifuga non gioca un ruolo significativo nella dinamica dell’oceano e dell’atmosfera, ma rende la Terra leggermente ellittica.

La forza di Coriolis è una pseudo-forza che emerge quando un oggetto si muove sulla superficie di un corpo in rotazione. La forza di Coriolis è concettualmente molto più sottile della forza centrifuga e, infatti, consiste in due effetti diversi, ciascuno illustrato qui sotto:

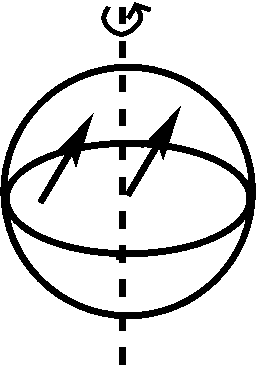
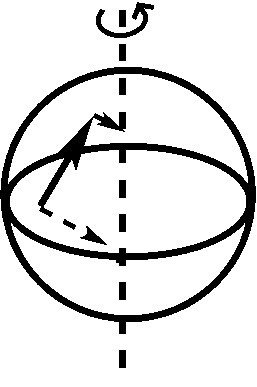
Il pannello di sinistra illustra il primo effetto: un oggetto che continua a muoversi nella stessa direzione nello spazio assoluto sembra cambiare direzione, mentre la Terra gira verso destra. All’inizio, l’oggetto si muove dritto verso nord, verso il polo (freccia sinistra), ma poi, la direzione del movimento diventa Nord-Est nel quadro di riferimento della Terra (freccia destra), anche se la direzione e la velocità dell’oggetto non sono cambiate nello spazio assoluto. Il pannello di destra illustra il secondo effetto: quando un oggetto si muove sulla superficie terrestre (come indicato dalla freccia solida), porta con sé la velocità della rotazione terrestre (frecce tratteggiate). Quando l’oggetto si muove verso nord, entra in regioni dove la velocità di rotazione terrestre è più piccola che nella sua posizione originale. Così, avrà un eccesso di velocità verso est che devia il movimento da nord verso nord-est, quando visto nel quadro di riferimento terrestre. Nel quadro di riferimento terrestre, ognuno di questi 2 effetti porta ad un’accelerazione con una grandezza uguale a \(\mega \volume v \sin\theta \) (con \(\mega \) la velocità angolare della Terra, \(v\) la velocità dell’oggetto nel quadro di riferimento terrestre, e \(\theta\) la latitudine), quindi l’accelerazione totale si somma a \(2 volte \mega \times v \sin\theta\) o \(f \times v\), con il parametro di Coriolis \(f = 2 volte \mega \times \sin\theta\). La forza di Coriolis è ad un angolo di \90^{circ} rispetto al movimento dell’oggetto, a destra nell’emisfero nord, a sinistra nell’emisfero sud; svanisce all’equatore (\theta=0\)). Nelle direzioni zonale e meridiana, le accelerazioni ammontano a:

\

L’impatto della forza di Coriolis su pacchetti d’aria (o acqua) in movimento è dimostrato qui.