Un rapport compare des valeurs.
Un rapport dit quelle quantité d’une chose il y a par rapport à une autre chose.

Il y a 3 carrés bleus pour 1 carré jaune
Les rapports peuvent être représentés de différentes manières :
| Utiliser le » : » pour séparer les valeurs : | 3 : 1 | |
| Ou on peut utiliser le mot » à » : | 3 à 1 | |
| Ou l’écrire comme une fraction : | 31 |
Un rapport peut être mis à l’échelle :
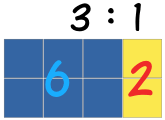
Ici le rapport est aussi de 3 carrés bleus pour 1 carré jaune,
même s’il y a plus de carrés.
Utilisation des ratios
L’astuce avec les ratios est de toujours multiplier ou diviser les nombres par la même valeur.
Exemple:
|
4 : 5 est identique à 4×2 : 5×2 = 8 : 10 |
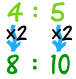 |
Recettes
Exemple : Une recette de crêpes utilise 3 tasses de farine et 2 tasses de lait.
Donc le ratio farine/lait est de 3 : 2
Pour faire des crêpes pour BEAUCOUP de personnes, nous pourrions avoir besoin de 4 fois la quantité, donc nous multiplions les chiffres par 4 :
3×4 : 2×4 = 12 : 8
En d’autres termes, 12 tasses de farine et 8 tasses de lait.
Le ratio est toujours le même, donc les crêpes devraient être tout aussi délicieuses.
Ratios « partie à partie » et « partie à tout »
Les exemples jusqu’à présent étaient « partie à partie » (comparer une partie à une autre partie).
Mais un ratio peut aussi montrer une partie par rapport au lot entier.
Exemple : Il y a 5 chiots, 2 sont des garçons et 3 des filles

Part-to-Part:
Le rapport entre les garçons et les filles est de 2:3 ou 2/3
Le rapport entre les filles et les garçons est de 3:2 ou 3/2
Part-to-Whole :
Le rapport entre les garçons et l’ensemble des petits est de 2:5 ou 2/5
Le rapport entre les filles et l’ensemble des petits est de 3:5 ou 3/5
Essayez vous-même
Nous pouvons utiliser les rapports pour augmenter ou diminuer l’échelle des dessins (en multipliant ou en divisant).
|
Le rapport hauteur/largeur du drapeau indien est de 2:3 Donc pour chaque 2 (pouces, mètres, peu importe) de hauteur |
 |
|
Si nous avons fait le drapeau de 20 pouces de haut, il devrait être de 30 pouces de large. Si nous faisions le drapeau de 40 cm de haut, il devrait avoir 60 cm de large (ce qui est toujours dans le rapport 2:3) |
|
Exemple : Pour dessiner un cheval à 1/10e de la taille normale, multipliez toutes les tailles par 1/10e
Ce cheval dans la vie réelle mesure 1500 mm de haut et 2000 mm de long, le rapport de sa hauteur sur sa longueur est donc
1500 : 2000
Quel est ce rapport lorsque nous le dessinons à 1/10e de sa taille normale ?
| 1500 : 2000 | ||
| = 150 : 200 |
On peut faire toutes les réductions/agrandissements que l’on veut de cette façon.
Un grand pied ?
 |
Allie a mesuré son pied et il faisait 21cm de long, puis elle a mesuré le pied de sa Mère et il faisait 24cm de long. |
« Je dois avoir de grands pieds, mon pied est presque aussi long que celui de ma Maman ! »
Mais elle a ensuite pensé à mesurer les hauteurs, et a constaté qu’elle mesure 133 cm, et que sa Maman mesure 152 cm.
Dans un tableau, cela donne :
| Allie | Maman | |
| Longueur du pied : | 21cm | 24cm |
| Hauteur : | 133cm | 152cm |
Le rapport « pied/hauteur » dans le style fractionné est de :
| Allie: | 21133 | Maman : | 24152 |
Donc le rapport pour Allie est 21 : 133
C’est toujours le même rapport, non ? Parce que nous avons divisé les deux nombres par la même quantité.
Et le rapport pour maman est 24 : 152
Cette fois, nous avons divisé par 8, mais ce rapport reste également le même.
Les rapports simplifiés « pieds/taille » sont maintenant :
| Allie : | 319 | Maman: | 319 |
« Oh ! » dit-elle, » les Ratios sont les mêmes « .
» Donc mon pied est seulement aussi grand qu’il devrait l’être pour ma taille, et n’est pas vraiment trop grand. «
