En général, un matériau ne peut pas se polariser instantanément en réponse à un champ appliqué, et donc la formulation plus générale en fonction du temps est
P ( t ) = ε 0 ∫ – ∞ t χ ( t – t ′ ) E ( t ′ ) d t ′ . {\displaystyle \mathbf {P} (t)=\varepsilon _{0}\int _{-\infty }^{t}\chi \left(t-t’\right)\mathbf {E} \left(t’\right)\,dt’.}

C’est-à-dire que la polarisation est une convolution du champ électrique aux temps précédents avec la susceptibilité dépendant du temps donnée par χ(Δt). La limite supérieure de cette intégrale peut également être étendue à l’infini si l’on définit χ(Δt) = 0 pour Δt < 0. Une réponse instantanée correspondrait à une susceptibilité de fonction delta de Dirac χ(Δt) = χδ(Δt).
Il est pratique de prendre la transformée de Fourier par rapport au temps et d’écrire cette relation en fonction de la fréquence. En raison du théorème de convolution, l’intégrale devient un simple produit,
P ( ω ) = ε 0 χ ( ω ) E ( ω ) . {\displaystyle \mathbf {P} (\omega )=\varepsilon _{0}\chi (\omega )\mathbf {E} (\omega ).}

Cette dépendance en fréquence de la susceptibilité entraîne une dépendance en fréquence de la permittivité. La forme de la susceptibilité par rapport à la fréquence caractérise les propriétés de dispersion du matériau.
De plus, le fait que la polarisation ne puisse dépendre du champ électrique qu’aux instants précédents (c’est-à-dire. effectivement χ(Δt) = 0 pour Δt < 0), une conséquence de la causalité, impose des contraintes de Kramers-Kronig sur la susceptibilité χ(0).
La permittivité complexeEdit
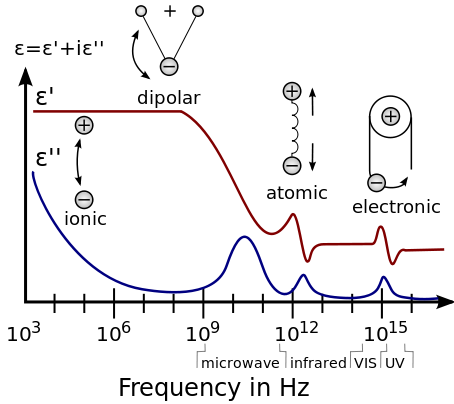
Par opposition à la réponse du vide, la réponse des matériaux normaux aux champs externes dépend généralement de la fréquence du champ. Cette dépendance en fréquence reflète le fait que la polarisation d’un matériau ne change pas instantanément lorsqu’un champ électrique est appliqué. La réponse doit toujours être causale (survenant après le champ appliqué), ce qui peut être représenté par une différence de phase. Pour cette raison, la permittivité est souvent traitée comme une fonction complexe de la fréquence (angulaire) ω du champ appliqué :
ε → ε ^ ( ω ) {\displaystyle \varepsilon \rightarrow {\hat {\varepsilon }}(\omega )}.

(puisque les nombres complexes permettent de spécifier la magnitude et la phase). La définition de la permittivité devient donc
D 0 e – i ω t = ε ^ ( ω ) E 0 e – i ω t , {\displaystyle D_{0}e^{-i\omega t}={\hat {\varepsilon }}(\omega )E_{0}e^{-i\omega t},}

où
- D0 et E0 sont les amplitudes des champs de déplacement et électrique, respectivement,
- i est l’unité imaginaire, i2 = -1.
La réponse d’un milieu aux champs électriques statiques est décrite par la limite basse fréquence de la permittivité, appelée aussi permittivité statique εs (également εDC) :
ε s = lim ω → 0 ε ^ ( ω ) . {\displaystyle \varepsilon _{\mathrm {s} }=\lim _{\omega \rightarrow 0}{\hat {\varepsilon }}(\omega ).}

À la limite des hautes fréquences (c’est-à-dire les fréquences optiques), la permittivité complexe est communément appelée ε∞ (ou parfois εopt). À la fréquence du plasma et en dessous, les diélectriques se comportent comme des métaux idéaux, avec un comportement de gaz d’électrons. La permittivité statique est une bonne approximation pour les champs alternatifs de basses fréquences, et lorsque la fréquence augmente, une différence de phase mesurable δ émerge entre D et E. La fréquence à laquelle le déphasage devient perceptible dépend de la température et des détails du milieu. Pour une intensité de champ modérée (E0), D et E restent proportionnels, et
ε ^ = D 0 E 0 = | ε | e – i δ . {\displaystyle {\hat {\varepsilon }}={\frac {D_{0}}{E_{0}}}=|\varepsilon |e^{-i\delta }.}

Puisque la réponse des matériaux aux champs alternatifs est caractérisée par une permittivité complexe, il est naturel de séparer ses parties réelle et imaginaire, ce qui est fait par convention de la manière suivante :
ε ^ ( ω ) = ε ′ ( ω ) – i ε ″ ( ω ) = | D 0 E 0 | ( cos δ – i sin δ ) . {\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon ‘(\omega )-i\varepsilon »(\omega )=\left|{\frac {D_{0}}{E_{0}}\right|\left(\cos \delta -i\sin \delta \right).}

ourquoi pas ?}
où
- ε′ est la partie réelle de la permittivité;
- ε″ est la partie imaginaire de la permittivité;
- δ est l’angle de perte.
Le choix du signe pour la dépendance temporelle, e-iωt, dicte la convention de signe pour la partie imaginaire de la permittivité. Les signes utilisés ici correspondent à ceux couramment utilisés en physique, alors que pour la convention d’ingénierie, il faut inverser toutes les quantités imaginaires.
La permittivité complexe est généralement une fonction compliquée de la fréquence ω, car elle est une description superposée des phénomènes de dispersion se produisant à plusieurs fréquences. La fonction diélectrique ε(ω) ne doit avoir des pôles que pour les fréquences à parties imaginaires positives, et satisfait donc les relations de Kramers-Kronig. Cependant, dans les plages de fréquences étroites qui sont souvent étudiées dans la pratique, la permittivité peut être approximée comme indépendante de la fréquence ou par des fonctions modèles.
À une fréquence donnée, la partie imaginaire, ε″, conduit à une perte d’absorption si elle est positive (dans la convention de signe ci-dessus) et à un gain si elle est négative. Plus généralement, il faut considérer les parties imaginaires des valeurs propres du tenseur diélectrique anisotrope.
Dans le cas des solides, la fonction diélectrique complexe est intimement liée à la structure de bande. La principale quantité qui caractérise la structure électronique de tout matériau cristallin est la probabilité d’absorption des photons, qui est directement liée à la partie imaginaire de la fonction diélectrique optique ε(ω). La fonction diélectrique optique est donnée par l’expression fondamentale:
ε ( ω ) = 1 + 8 π 2 e 2 m 2 ∑ c , v ∫ W c , v ( E ) ( φ ( ℏ ω – E ) – φ ( ℏ ω + E ) ) d x . {\displaystyle \varepsilon (\omega )=1+{\frac {8\pi ^{2}e^{2}}{m^{2}}}\sum _{c,v}\int W_{c,v}(E){\bigl (}\varphi (\hbar \omega -E)-\varphi (\hbar \omega +E){\bigr )}\,dx.}

Dans cette expression, Wc,v(E) représente le produit de la probabilité de transition moyennée par la zone de Brillouin à l’énergie E avec la densité d’états conjointe, Jc,v(E) ; φ est une fonction d’élargissement, représentant le rôle de la diffusion dans l’étalement des niveaux d’énergie. En général, l’élargissement est intermédiaire entre Lorentzien et Gaussien ; pour un alliage, il est un peu plus proche de Gaussien en raison de la forte diffusion due aux fluctuations statistiques de la composition locale à l’échelle nanométrique.
La permittivité tensorielleEdit
Selon le modèle de Drude de plasma magnétisé, une expression plus générale qui prend en compte l’interaction des porteurs avec un champ électrique alternatif aux fréquences millimétriques et micro-ondes dans un semi-conducteur magnétisé axialement nécessite l’expression de la permittivité comme un tenseur non diagonal. (voir aussi Electro-gyration).
D ( ω ) = | ε 1 – i ε 2 0 i ε 2 ε 1 0 0 0 ε z | E ( ω ) {\displaystyle \mathbf {D} (\omega )={\begin{vmatrix}\varepsilon _{1}&-i\varepsilon _{2}&0\\\i\\varepsilon _{2}&\varepsilon _{1}&&&\varepsilon _{z}\\\\N-end{vmatrix}\Notre nom d’opérateur {\mathbf {E}} } (\omega )}

Si ε2 disparaît, alors le tenseur est diagonal mais non proportionnel à l’identité et on dit que le milieu est un milieu uniaxial, qui a des propriétés similaires à un cristal uniaxial.
Classification des matériauxModification
| εr″/εr′ | Conduction du courant | Propagation du champ |
|---|---|---|
| 0 | diélectrique parfait milieu sans perte |
|
| ≪ 1 | matériau à faible…matériau de conductivité pauvre conducteur |
faible-perte bon diélectrique |
≈ 1 | Matériau conducteur à perte | moyen de propagation à perte |
| ≫ 1 | Matériau à haute conductivité bon conducteur |
moyen à fortes pertes .perte pauvre diélectrique |
| ∞ | conducteur parfait |
Les matériaux peuvent être classés en fonction de leur permittivité ε à valeur complexe, après comparaison de ses composantes réelles ε′ et imaginaires ε″ (ou, de manière équivalente, de leur conductivité, σ, lorsqu’elle est comptabilisée dans cette dernière). Un conducteur parfait a une conductivité infinie, σ = ∞, tandis qu’un diélectrique parfait est un matériau qui n’a aucune conductivité, σ = 0. Ce dernier cas, de permittivité à valeur réelle (ou de permittivité à valeur complexe avec une composante imaginaire nulle) est également associé au nom de milieux sans perte. En général, lorsque σ/ωε′ ≪ 1, nous considérons que le matériau est un diélectrique à faibles pertes (bien qu’il ne soit pas exactement sans pertes), tandis que σ/ωε′ ≫ 1 est associé à un bon conducteur ; de tels matériaux à conductivité non négligeable produisent une grande quantité de pertes qui inhibent la propagation des ondes électromagnétiques, et sont donc également appelés milieux à pertes. Les matériaux qui ne relèvent d’aucune des deux limites sont considérés comme des milieux généraux.
Milieu à pertesModifié
Dans le cas d’un milieu à pertes, c’est-à-dire lorsque le courant de conduction n’est pas négligeable, la densité de courant totale qui circule est :
J tot = J c + J d = σ E + i ω ε ′ E = i ω ε ^ E {\displaystyle J_{\text{tot}=J_{\mathrm {c} }+J_{\mathrm {d} }=\sigma E+i\omega \varepsilon ‘E=i\omega {\hat {\varepsilon }}E}

où
- σ est la conductivité du milieu ;
- ε ′ = ε 0 ε r {\displaystyle \varepsilon’=\varepsilon _{0}\varepsilon _{r}}.
est la partie réelle de la permittivité.
- ε ^ = ε ′ – i ε ″ {\displaystyle {\hat {\varepsilon }}=\varepsilon ‘-i\varepsilon »}.
est la permittivité complexe
La taille du courant de déplacement dépend de la fréquence ω du champ appliqué E ; il n’y a pas de courant de déplacement dans un champ constant.
Dans ce formalisme, la permittivité complexe est définie comme :
ε ^ = ε ′ ( 1 – i σ ω ε ′ ) = ε ′ – i σ ω {\displaystyle {\hat {\varepsilon }}=\varepsilon ‘\left(1-i{\frac {\sigma }{\omega \varepsilon ‘}\right)=\varepsilon ‘-i{\frac {\sigma }{\omega }}.

En général, l’absorption de l’énergie électromagnétique par les diélectriques est couverte par quelques mécanismes différents qui influencent la forme de la permittivité en fonction de la fréquence :
- Premièrement, les effets de relaxation associés aux dipôles moléculaires permanents et induits. Aux basses fréquences, le champ change assez lentement pour permettre aux dipôles d’atteindre l’équilibre avant que le champ n’ait changé de façon mesurable. Pour les fréquences auxquelles les orientations des dipôles ne peuvent suivre le champ appliqué en raison de la viscosité du milieu, l’absorption de l’énergie du champ entraîne une dissipation d’énergie. Le mécanisme de relaxation des dipôles est appelé relaxation diélectrique et pour les dipôles idéaux, il est décrit par la relaxation classique de Debye.
- Deuxièmement, il y a les effets de résonance, qui proviennent des rotations ou des vibrations des atomes, des ions ou des électrons. Ces processus sont observés au voisinage de leurs fréquences d’absorption caractéristiques.
Les effets ci-dessus se combinent souvent pour provoquer des effets non linéaires au sein des condensateurs. Par exemple, l’absorption diélectrique désigne l’incapacité d’un condensateur qui a été chargé pendant une longue période à se décharger complètement lorsqu’il est brièvement déchargé. Bien qu’un condensateur idéal resterait à zéro volt après avoir été déchargé, les condensateurs réels développent une petite tension, un phénomène qui est également appelé absorption ou effet de batterie. Pour certains diélectriques, comme de nombreux films polymères, la tension résultante peut être inférieure à 1-2 % de la tension d’origine. Cependant, elle peut atteindre 15 à 25 % dans le cas des condensateurs électrolytiques ou des supercondensateurs.
Interprétation de la mécanique quantiqueEdit
En termes de mécanique quantique, la permittivité s’explique par les interactions atomiques et moléculaires.
Au niveau des basses fréquences, les molécules des diélectriques polaires sont polarisées par un champ électrique appliqué, ce qui induit des rotations périodiques. Par exemple, à la fréquence micro-ondes, le champ micro-ondes provoque la rotation périodique des molécules d’eau, suffisante pour rompre les liaisons hydrogène. Le champ agit contre les liaisons et l’énergie est absorbée par le matériau sous forme de chaleur. C’est pourquoi les fours à micro-ondes fonctionnent très bien pour les matériaux contenant de l’eau. Il existe deux maxima de la composante imaginaire (l’indice d’absorption) de l’eau, l’un à la fréquence des micro-ondes, et l’autre à la fréquence de l’ultraviolet lointain (UV). Ces deux résonances se situent à des fréquences supérieures à la fréquence de fonctionnement des fours à micro-ondes.
À des fréquences modérées, l’énergie est trop élevée pour provoquer une rotation, mais trop faible pour affecter directement les électrons, et est absorbée sous la forme de vibrations moléculaires résonantes. Dans l’eau, c’est là que l’indice d’absorption commence à diminuer fortement, et le minimum de la permittivité imaginaire se situe à la fréquence de la lumière bleue (régime optique).
Au niveau des hautes fréquences (comme les UV et plus), les molécules ne peuvent pas se relaxer, et l’énergie est purement absorbée par les atomes, excitant les niveaux d’énergie des électrons. Ainsi, ces fréquences sont classées comme des rayonnements ionisants.
Bien que la réalisation d’une modélisation ab initio (c’est-à-dire de premiers principes) complète soit désormais possible sur le plan informatique, elle n’a pas encore été largement appliquée. Ainsi, un modèle phénoménologique est accepté comme étant une méthode adéquate pour capturer les comportements expérimentaux. Le modèle de Debye et le modèle de Lorentz utilisent une représentation linéaire des paramètres d’un système forfaitaire du premier ordre et du second ordre (respectivement) (comme un circuit résonnant RC et un circuit résonnant LRC).

