Automates finis déterministes
Un automate fini déterministe (AFD) est décrit par un tuple à cinq éléments : (Q,Σ,δ,q0,F)(Q, \Sigma, \delta, q_0, F)(Q,Σ,δ,q0,F).
QQQQ = un ensemble fini d’états
Σ\SigmaΣ = un alphabet d’entrée fini, non vide
δ\deltaδ = une série de fonctions de transition
q0q_0q0 = l’état de départ
FFF = l’ensemble des états acceptants
Il doit y avoir exactement une fonction de transition pour chaque symbole d’entrée dans Σ\SigmaΣ de chaque état.
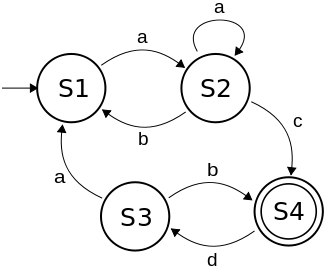
Les ADF peuvent être représentés par des diagrammes de cette forme : 
Quelle chaîne de caractères ne peut pas être générée par la machine à états finis ci-dessous ?
Voici un diagramme DFA qui décrit quelques mouvements simples qu’un personnage dans un jeu vidéo peut faire : se tenir debout, courir et sauter. Les boutons qu’un joueur peut utiliser pour contrôler ce personnage particulier sont « Up », « A », ou le joueur peut n’appuyer sur aucun bouton.

En utilisant le diagramme d’état du personnage de jeu vidéo ci-dessus, décrivez comment un joueur peut contrôler son personnage pour passer de la position debout à la course et au saut.
Show AnswerDans l’état debout, le joueur peut ne rien appuyer et rester dans l’état debout, puis, pour passer à l’état de course, l’utilisateur doit appuyer sur le bouton « Up ». Dans l’état de course, l’utilisateur peut continuer à faire courir son personnage en appuyant sur le bouton « Up », puis, pour passer à l’état de saut, l’utilisateur doit appuyer sur « A. »
Dessinez un diagramme pour un DFA qui reconnaît le langage suivant : Le langage de toutes les chaînes de caractères qui se terminent par un 1.
Montrer la réponse
Automates finis non déterministes
QQQ = un ensemble fini d’états
Σ\SigmaΣ = un alphabet d’entrée fini, non vide
δ\deltaδ = une série de fonctions de transition
q0q_0q0 = l’état de départ
FFF = l’ensemble des états acceptants
Contrairement aux DFA, les NDFA ne sont pas obligés d’avoir des fonctions de transition pour chaque symbole dans Σ\SigmaΣ, et il peut y avoir plusieurs fonctions de transition dans le même état pour le même symbole. De plus, les ADFN peuvent utiliser des transitions nulles, qui sont indiquées par ϵ\epsilonϵ. Les transitions nulles permettent à la machine de sauter d’un état à un autre sans avoir à lire un symbole.
Une NDFA accepte une chaîne xxx s’il existe un chemin compatible avec cette chaîne qui se termine dans un état d’acceptation.
Les APDFN peuvent être représentés par des diagrammes de cette forme :
 source
source
Décrivez le langage que l’ANFD ci-dessus reconnaît.
Show AnswerLe NDFA ci-dessus reconnaît les chaînes de caractères qui se terminent par « 10 » et celles qui se terminent par « 01 ».
L’état aaa est l’état de départ, et à partir de là, nous pouvons créer une chaîne de caractères avec n’importe quel nombre de 1 et de 0 dans n’importe quel ordre, puis passer à l’état bbb ou à l’état eee, ou nous pouvons passer immédiatement à l’état bbb ou à l’état eee. Dans tous les cas, le NDFA n’acceptera qu’une chaîne qui atteint l’état ddd ou l’état ggg. Pour atteindre l’état ddd ou l’état ggg, la chaîne doit se terminer par un « 01 » (pour l’état ddd) ou un « 10 » (pour l’état ggg).
Par exemple, les chaînes suivantes sont toutes reconnues par ce NDFA.
- 00000000010
- 10
- 01
- 1111101
Quelle chaîne de caractères ne peut pas être générée par la machine à états finis ci-dessous ?

Dessinez un diagramme pour l’APDFN qui décrit le langage suivant : Le langage de toutes les chaînes qui se terminent par un 1.
Show Answer
.

