Introduction à la chimie – 1ère édition canadienne

Les gaz ont été parmi les premières substances étudiées à l’aide de la méthode scientifique moderne, qui a été développée dans les années 1600. Il n’a pas fallu longtemps pour reconnaître que les gaz partageaient tous certains comportements physiques, suggérant que les gaz pouvaient être décrits par une seule théorie globale. La théorie cinétique moléculaire des gaz est un modèle qui nous aide à comprendre les propriétés physiques des gaz au niveau moléculaire. Elle est basée sur les concepts suivants :

1. Les gaz sont constitués de particules (molécules ou atomes) qui sont en mouvement aléatoire constant.
2. Les particules de gaz entrent constamment en collision entre elles et avec les parois de leur récipient. Ces collisions sont élastiques, c’est-à-dire qu’il n’y a pas de perte nette d’énergie lors des collisions.
3. Les particules de gaz sont petites et le volume total occupé par les molécules de gaz est négligeable par rapport au volume total de leur contenant.
4. Il n’y a pas de forces interactives (c’est-à-dire, attraction ou répulsion) entre les particules d’un gaz.
5. L’énergie cinétique moyenne des particules de gaz est proportionnelle à la température absolue du gaz, et tous les gaz à la même température ont la même énergie cinétique moyenne.

Figure 6.6 « La théorie moléculaire cinétique des gaz » montre une représentation de la façon dont nous nous représentons mentalement la phase gazeuse.

La théorie moléculaire cinétique des gaz décrit cet état de la matière comme étant composé de minuscules particules en mouvement constant avec beaucoup de distance entre les particules. Comme la majeure partie du volume occupé par un gaz est un espace vide, un gaz a une faible densité et peut se dilater ou se contracter sous l’influence appropriée. Le fait que les particules de gaz soient en mouvement constant signifie que deux gaz ou plus se mélangeront toujours, car les particules des différents gaz se déplacent et entrent en collision les unes avec les autres. Le nombre de collisions que les particules de gaz font avec les parois de leur récipient et la force avec laquelle elles entrent en collision déterminent l’ampleur de la pression du gaz.

Energie cinétique et vitesse moléculaire

Les particules de gaz sont en mouvement constant, et tout objet en mouvement possède une énergie cinétique (Ek). L’énergie cinétique, pour un atome individuel, peut être calculée par l’équation suivante où m est la masse et u la vitesse.

Ek = 1/2 mu2

Dans l’ensemble, les molécules d’un échantillon de gaz partagent une énergie cinétique moyenne ; cependant, les molécules individuelles présentent une distribution des énergies cinétiques parce qu’elles ont une distribution des vitesses (figure 6.7  » Distribution stylisée des vitesses moléculaires « ). Cette distribution des vitesses provient des collisions qui se produisent entre les molécules dans la phase gazeuse. Bien que ces collisions soient élastiques (il n’y a pas de perte nette d’énergie), les vitesses individuelles de chaque molécule impliquée dans la collision peuvent changer. Par exemple, dans la collision de deux molécules, une molécule peut être déviée à une vitesse légèrement supérieure et l’autre à une vitesse légèrement inférieure, mais l’énergie cinétique moyenne ne change pas.

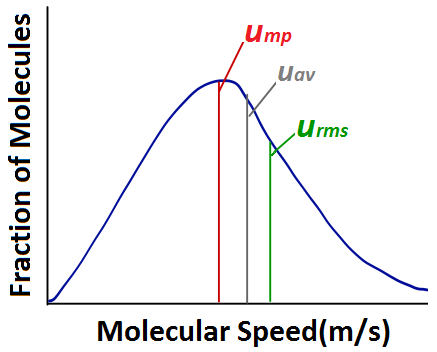
Lorsqu’on analyse un diagramme de la distribution des vitesses moléculaires, il faut se familiariser avec plusieurs termes couramment utilisés. La vitesse la plus probable (ump) est la vitesse du plus grand nombre de molécules, et correspond au pic de la distribution. La vitesse moyenne (uav) est la vitesse moyenne de toutes les molécules de gaz dans l’échantillon. La vitesse moyenne quadratique (urms) correspond à la vitesse des molécules ayant exactement la même énergie cinétique que l’énergie cinétique moyenne de l’échantillon.

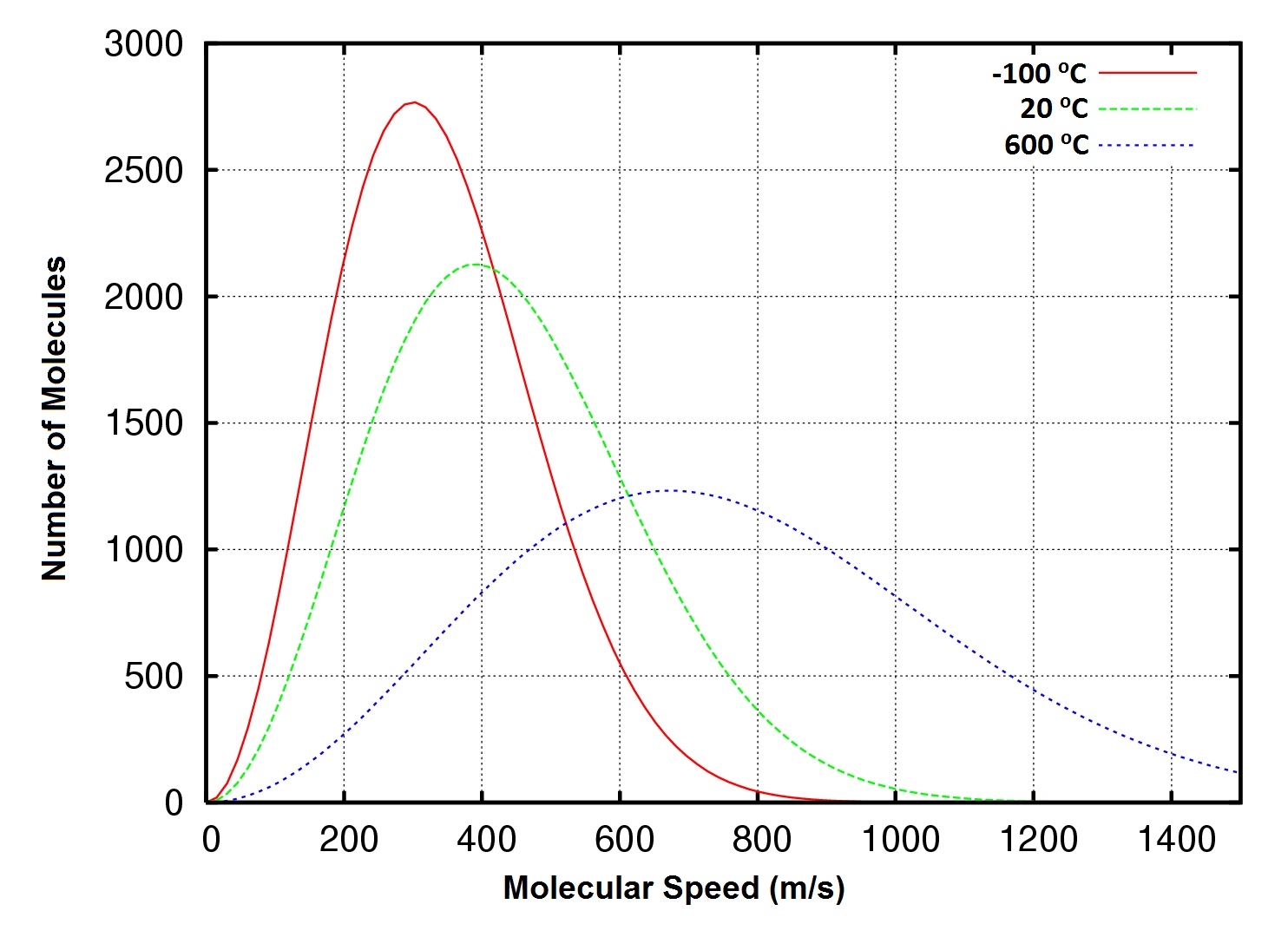
Figure 6.8 Distribution des vitesses moléculaires, oxygène gazeux à -100, 20 et 600°C

Selon la théorie cinétique moléculaire, l’énergie cinétique moyenne des particules de gaz est proportionnelle à la température absolue du gaz. Ceci peut être exprimé par l’équation suivante où k représente la constante de Boltzmann. La constante de Boltzmann est simplement la constante des gaz R divisée par la constante d’Avogadro (NA). La barre au-dessus de certains termes indique qu’il s’agit de valeurs moyennes.

\overline{E_k} = \frac{3}{2} \textit{kT}

Puisque l’énergie cinétique moyenne est liée à la fois à la température absolue et à la vitesse moléculaire, nous pouvons combiner l’équation ci-dessus avec la précédente pour déterminer la vitesse efficace.

Superline{E_k}. \textit{ = }\frac{1}{2} \textit{m} \overline{u^2} \textit{ = } \frac{3}{2} \textit{kT}

$\sqrt{\overline{u^2}} = \sqrt{\frac{3kT}{m}}$

Cela démontre que la vitesse efficace est liée à la température. Nous pouvons encore manipuler cette équation en multipliant le numérateur et le dénominateur par la constante d’Avogadro (NA) pour nous donner une forme utilisant la constante des gaz (R) et la masse molaire (M).

$\sqrt{\overline{u^2}}\ = \sqrt{\frac{3RT}{M}}$

Cette forme de l’équation démontre que la vitesse efficace des molécules de gaz est également liée à la masse molaire de la substance. En comparant deux gaz de masse molaire différente à la même température, on constate que malgré une énergie cinétique moyenne identique, le gaz ayant la plus petite masse molaire aura une vitesse efficace plus élevée.

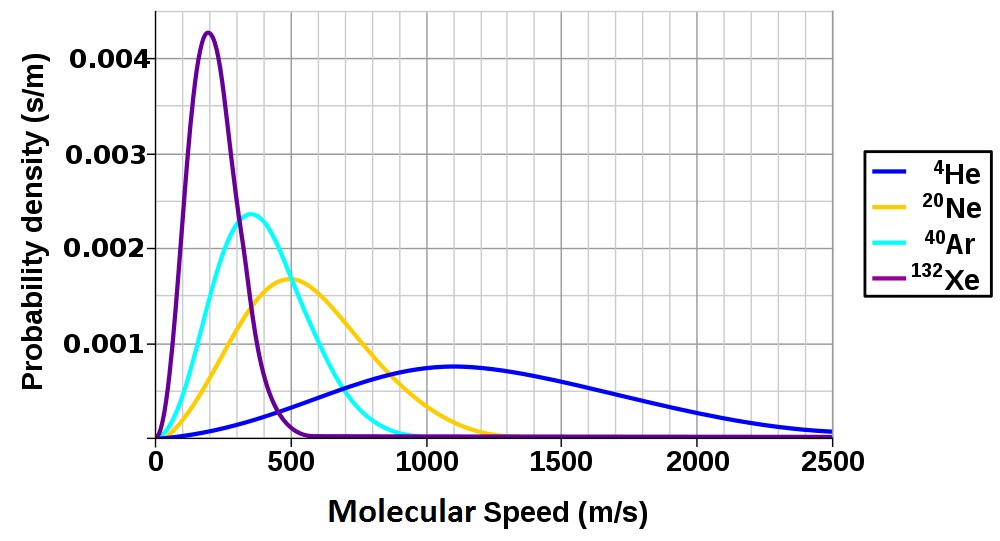
Figure 6.9 Distribution de la vitesse moléculaire des gaz nobles

Application de la théorie cinétique moléculaire aux lois sur les gaz

La théorie cinétique moléculaire peut être utilisée pour expliquer ou prédire les tendances expérimentales qui ont été utilisées pour générer les lois sur les gaz. Travaillons sur quelques scénarios pour démontrer ce point.

Que va-t-il se passer pour la pression d’un système dont le volume est diminué à température constante ?

Ce problème peut être abordé de deux façons :

1. La loi des gaz idéaux peut être réarrangée pour résoudre la pression et estimer le changement de pression :

\textit{PV = nRT}

\textit{P = }\frac{nRT}{V}\textit{}

Le volume est situé au dénominateur de l’équation, et il est diminué. Cela signifie que le reste de l’équation est divisé par un nombre plus petit, ce qui devrait donc rendre la pression plus grande.

2. On peut utiliser la théorie cinétique moléculaire. Puisque la température reste constante, l’énergie cinétique moyenne et la vitesse efficace restent également les mêmes. Le volume du récipient a diminué, ce qui signifie que les molécules de gaz doivent parcourir une distance plus courte pour avoir une collision. Il y aura donc plus de collisions par seconde, ce qui entraînera une augmentation de la pression.

Que se passera-t-il pour la pression d’un système où la température est augmentée et où le volume reste constant ?

Encore, ce type de problème peut être abordé de deux manières :

1. La loi des gaz idéaux peut être réarrangée pour résoudre la pression et estimer le changement de pression.

{p = }\frac{nRT}{V}\textit{}

La température est située au numérateur ; il existe une relation directe entre la température et la pression. Par conséquent, une augmentation de la température devrait entraîner une augmentation de la pression.

2. On peut utiliser la théorie cinétique moléculaire. La température est augmentée, donc l’énergie cinétique moyenne et la vitesse efficace devraient également augmenter. Cela signifie que les molécules de gaz vont frapper les parois du récipient plus fréquemment et avec plus de force car elles se déplacent toutes plus rapidement. Cela devrait augmenter la pression.

.