Introduction
Cette page traite des contraintes et déformations principales.Bien que nous n’ayons pas encore abordé les nombreuses définitions différentes des contraintes et déformations,il est en fait vrai que tout ce qui est abordé ici s’applique quel que soit le type de tenseur de contrainte ou de déformation. Par exemple, si vous calculez les valeurs principales d’un tenseur de contraintes de Cauchy, vous obtenez les contraintes principales de Cauchy. Les valeurs principales d’un tenseur de déformation de Green seront des déformations principales de Green.
Tout ce qui suit découle de deux faits : Premièrement, les tenseurs de contraintes et de déformations d’entrée sont symétriques.Deuxièmement, les transformations de coordonnées discutées ici sont applicables aux tenseurs de contraintes et de déformations (elles le sont effectivement).
Nous parlerons d’abord des contraintes, puis des déformations.
Contraintes principales en 2-D

En 2-D, les équations de transformation sont
\
Ce sont les formes développées de \(\boldsymbol{\sigma}’ = {\bf Q} \cdot \boldsymbol{\sigma} \cdot {\bf Q}^T\) en 2-D.Elles peuvent également être dérivées d’un bilan de force de la figure présentée ici. Il est intéressant que la contrainte soit caractérisée comme un tenseur car elle suit l’équation de transformation. Mais il s’agit avant tout d’un argument mathématique, qui aurait peu de poids s’il n’était pas lié à la physique de l’équilibre des forces. Le fait que l’équation de transformation des coordonnées reflète correctement l’équilibre des forces à différentes orientations est ce qui le rend pertinent.
Les contraintes principales sont les contraintes normales correspondantes à un angle, \(\theta_P\), auquel la contrainte de cisaillement, \(\tau’_{xy}\), est nulle.
Cette page effectue des transformations tensorielles complètes en 3-D, mais peut toujours être utilisée pour des problèmes en 2-D…. Saisissez les valeurs dans les positions 2×2 en haut à gauche et effectuez une rotation dans le plan 1-2 pour effectuer des transformations en 2-D. La capture d’écran ci-dessous montre un cas de cisaillement pur tourné à 45° pour obtenir les contraintes principales. Notez également comment la matrice \({\bf Q}\) se transforme.
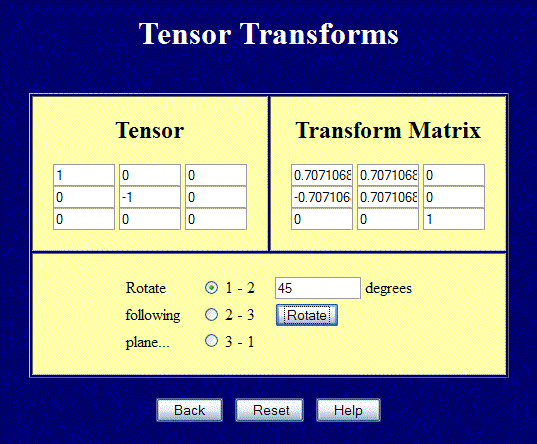
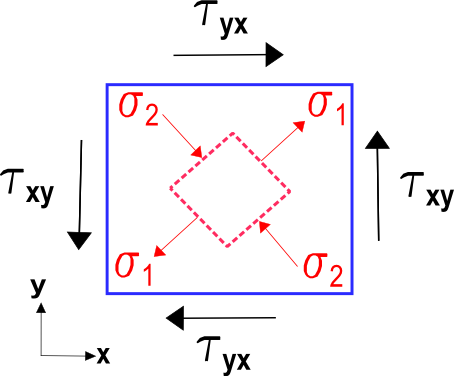
La figure ci-dessous montre les contraintes correspondant au cas de cisaillement pur dans l’exemple de page web de transformation tensorielle. Le carré bleu aligné avec les axes subit clairement un cisaillement.Mais le carré rouge inscrit dans le plus grand carré bleu ne voit que de simples tensions et compressions.Ce sont les valeurs principales du cas de cisaillement pur dans le système de coordonnées global.
En 2-D, l’orientation de la contrainte principale, \(\theta_P\), peut être calculée en mettant \(\tau’\!_{xy} = 0\) dans l’équation de cisaillement ci-dessus et en résolvant pour \(\theta\)pour obtenir \(\theta_P\), l’angle de contrainte principale.
Cela donne
La matrice de transformation, \({\bf Q}\), est
\\\]
Insérer cette valeur pour \(\theta_P\) de nouveau dans les équations pour les contraintes normales donne les valeurs principales. Elles s’écrivent comme \(\sigma_{max}\) et \(\sigma_{min}\), ou alternativement comme \(\sigma_1\) et \(\sigma_2\).
Ils pourraient également être obtenus en utilisant \(\boldsymbol{\sigma}’ = {\bf Q} \cdot \boldsymbol{\sigma} \cdot {\bf Q}^T\)avec \({\bf Q}\) basé sur \(\theta_P\).
Contraintes principales en 3-D
Les transformations de coordonnées en 3-D sont
\ = \left\left\]
La seconde matrice \({\bf Q}\) est à nouveau la transposée de la première.
Cette page effectue des transformations tensorielles.
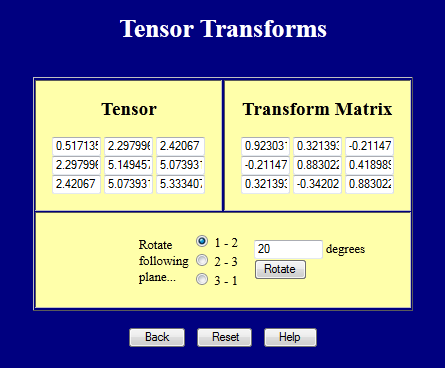
Et cette page calcule les valeurs principales (valeurs propres)et les directions principales (vecteurs propres).
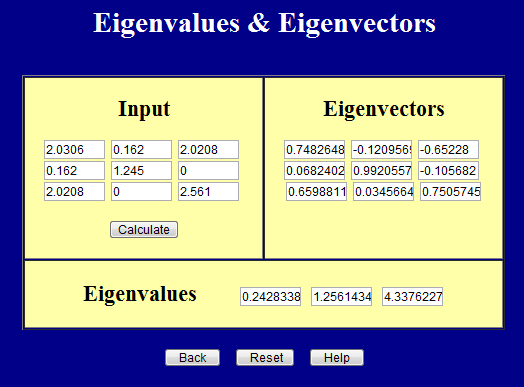
Il est important de se rappeler que les entrées des deux pages doivent être symétriques. En fait, les deux pages l’imposent.
Les valeurs propres ci-dessus peuvent être écrites sous forme de matrice comme
\]
D Déformations principales 2-D
La mécanique du calcul des déformations principales est identique à celle du calcul des contraintes principales. Le seul écueil potentiel à garder à l’esprit est que les équations opèrent toujours sur la moitié des valeurs de cisaillement, \(\gamma / 2\).
En 2-D, les équations de transformation sont
\
Les équations sont écrites en termes de \(\gamma / 2\) pour souligner que la moitié de toutes les valeurs de cisaillement sont utilisées dans les équations de transformation.
Cette page effectue des transformations tensorielles 3-D complètes,mais peut toujours être utilisée pour les problèmes 2-D… Entrez les valeurs dans les positions 2×2 en haut à gauche et tournez dans le plan 1-2 pour effectuer des transformations en 2-D. La capture d’écran ci-dessous montre un cas de cisaillement pur tourné à 45° pour obtenir les déformations principales. Notez également comment la matrice \({\bf Q}\) se transforme.

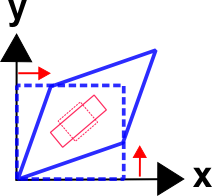
La figure ci-dessous montre les formes déformées correspondant au cas de cisaillement pur dans l’exemple de page web de transformation tensorielle. Le carré bleu aligné avec les axes subit clairement un cisaillement.Mais le carré rouge inscrit dans le plus grand carré bleu ne voit que de simples tensions et compressions.Ce sont les valeurs principales de la déformation de cisaillement pur dans le système de coordonnées global.
En 2-D, l’orientation principale de la déformation, \(\theta_P\), peut être calculée en mettant \(\gamma’\!_{xy} = 0\) dans l’équation de cisaillement ci-dessus et en résolvant pour \(\theta\)pour obtenir \(\theta_P\), l’angle principal de déformation.
Cela donne
La matrice de transformation, \({\bf Q}\), est
\\\]
En réinsérant cette valeur de \(\theta_P\) dans les équations des déformations normales, on obtient les valeurs principales. Elles s’écrivent \(\epsilon_{max}\) et \(\epsilon_{min}\), ou encore \(\epsilon_1\) et \(\epsilon_2\).
On pourrait également les obtenir en utilisant \({\bf E}’ = {\bf Q} \cdot {\bf E} \cdot {\bf Q}^T\)avec \({\bf Q}\) basé sur \(\theta_P\).
Déformations principales en 3-D
Les transformations de coordonnées en 3-D sont
\ = \left\left\]
La seconde matrice \({\bf Q}\) est à nouveau la transposée de la première.
Cette page effectue des transformations tensorielles.

Et cette page calcule les valeurs principales (valeurs propres)et les directions principales (vecteurs propres).

Il est important de se rappeler que les entrées des deux pages doivent être symétriques. En fait, les deux pages imposent cela.
Les valeurs propres ci-dessus peuvent être écrites sous forme matricielle comme
\\]
Sommaire
Ce principe de quantités invariantes sous les transformations de coordonnées esten fait universel à travers toutes les matrices qui sont symétriques et étant transforméesaccording to
\
où \({\bf A}\) est « toute matrice symétrique ».
Et rappelez-vous que le produit de toute matrice avec sa transposée est toujours un résultat symétrique, donc ce résultat serait qualifié. Ceci est particulièrement pertinent pour \({\bf F}^T \ ! \cdot {\bf F}\), dont les invariants sont utilisés dans la loi de Mooney-Rivlin sur le comportement du caoutchouc.La loi et les coefficients de Mooney-Rivlin seront discutés sur cette page.En guise d’accroche supplémentaire, nous verrons que le 3ème invariant de \({\bf F}^T \ ! \cdot {\bf F}\)pour le caoutchouc est toujours égal à 1 car le caoutchouc est incompressible. Donc non seulement c’est une constante,indépendante des transformations de coordonnées, mais c’est même une valeur constante, toujours égale à 1, indépendante des transformations de coordonnées et de l’état de déformation.
.