La nécessité de distinguer les différentes significations du « cadre de référence » a conduit à une variété de termes. Par exemple, parfois le type de système de coordonnées est attaché comme un modificateur, comme dans cadre de référence cartésien. Parfois, l’état de mouvement est mis en avant, comme dans le cadre de référence rotatif. Parfois, la façon dont il se transforme en cadres considérés comme apparentés est mise en avant, comme dans le cadre de référence galiléen. Parfois, les cadres sont distingués par l’échelle de leurs observations, comme dans les cadres de référence macroscopique et microscopique.
Dans cet article, le terme cadre de référence observationnel est utilisé lorsque l’accent est mis sur l’état de mouvement plutôt que sur le choix des coordonnées ou le caractère des observations ou de l’appareil d’observation. En ce sens, un cadre de référence observationnel permet l’étude de l’effet du mouvement sur une famille entière de systèmes de coordonnées qui pourraient être attachés à ce cadre. D’autre part, un système de coordonnées peut être utilisé à de nombreuses fins où l’état de mouvement n’est pas la préoccupation principale. Par exemple, un système de coordonnées peut être adopté pour tirer parti de la symétrie d’un système. Dans une perspective encore plus large, la formulation de nombreux problèmes de physique utilise des coordonnées généralisées, des modes normaux ou des vecteurs propres, qui ne sont qu’indirectement liés à l’espace et au temps. Il semble utile de divorcer les différents aspects d’un cadre de référence pour la discussion qui suit. Nous prenons donc les cadres de référence observationnels, les systèmes de coordonnées et les équipements observationnels comme des concepts indépendants, séparés comme ci-dessous :
- Un cadre observationnel (tel qu’un cadre de référence inertiel ou non inertiel) est un concept physique lié à l’état de mouvement.
- Un système de coordonnées est un concept mathématique, équivalant à un choix de langage utilisé pour décrire les observations. Par conséquent, un observateur dans un cadre de référence observationnel peut choisir d’employer n’importe quel système de coordonnées (cartésien, polaire, curviligne, généralisé, …) pour décrire les observations faites à partir de ce cadre de référence. Un changement dans le choix de ce système de coordonnées ne modifie pas l’état de mouvement de l’observateur, et n’entraîne donc pas de changement dans le cadre de référence observationnel de l’observateur. Ce point de vue se retrouve également ailleurs. Ce qui ne veut pas dire que certains systèmes de coordonnées peuvent être un meilleur choix pour certaines observations que d’autres.
- Le choix de ce qu’il faut mesurer et avec quel appareil d’observation est une question distincte de l’état de mouvement de l’observateur et du choix du système de coordonnées.
Voici une citation applicable aux cadres d’observation mobiles R {\displaystyle {\mathfrak {R}}}.

et aux divers systèmes de coordonnées euclidiens à trois espaces associés :
Nous introduisons d’abord la notion de référentiel, elle-même liée à l’idée d’observateur : le référentiel est, en quelque sorte, » l’espace euclidien porté par l’observateur « . Donnons une définition plus mathématique : … le cadre de référence est … l’ensemble de tous les points de l’espace euclidien portant le mouvement du corps rigide de l’observateur. Le cadre, noté R {\displaystyle {\mathfrak {R}}}.
, est dit se déplacer avec l’observateur…. Les positions spatiales des particules sont étiquetées par rapport à un cadre R {\displaystyle {\mathfrak {R}}}.
en établissant un système de coordonnées R avec une origine O. L’ensemble correspondant d’axes, partageant le mouvement du corps rigide du cadre R {\displaystyle {\mathfrak {R}}}.
, peut être considéré comme donnant une réalisation physique de R {\displaystyle {\mathfrak {R}}}.
. Dans un cadre R {\displaystyle {\mathfrak {R}}}
, on passe des coordonnées de R à R′ en effectuant, à chaque instant du temps, la même transformation de coordonnées sur les composantes des objets intrinsèques (vecteurs et tenseurs) introduits pour représenter les quantités physiques dans ce cadre.
et ceci sur l’utilité de séparer les notions de R {\displaystyle {\mathfrak {R}}}.

et :
Comme l’a noté Brillouin, il faut distinguer les ensembles de coordonnées mathématiques des référentiels physiques. L’ignorance de cette distinction est la source de beaucoup de confusion… les fonctions dépendantes comme la vitesse par exemple, sont mesurées par rapport à un référentiel physique, mais on est libre de choisir n’importe quel système de coordonnées mathématiques dans lequel les équations sont spécifiées.
et ceci, également sur la distinction entre R {\displaystyle {\mathfrak {R}}}}.

et :
L’idée d’un cadre de référence est vraiment très différente de celle d’un système de coordonnées. Les cadres diffèrent juste lorsqu’ils définissent des espaces (ensembles de points de repos) ou des temps (ensembles d’événements simultanés) différents. Les idées d’espace, de temps, de repos et de simultanéité sont donc inextricablement liées à celle de cadre. Cependant, un simple déplacement de l’origine, ou une rotation purement spatiale des coordonnées spatiales, donne lieu à un nouveau système de coordonnées. Les cadres correspondent donc au mieux à des classes de systèmes de coordonnées.
et de J. D. Norton:
Dans les développements traditionnels de la relativité restreinte et générale, il a été habituel de ne pas distinguer deux idées bien distinctes. La première est la notion de système de coordonnées, comprise simplement comme l’attribution lisse et inversible de quatre nombres aux événements dans les voisinages de l’espace-temps. La seconde, le cadre de référence, fait référence à un système idéalisé utilisé pour attribuer ces nombres. Pour éviter des restrictions inutiles, nous pouvons divorcer cet arrangement des notions métriques. Il est particulièrement important pour notre propos que chaque cadre de référence ait un état de mouvement défini pour chaque événement de l’espace-temps. Dans le contexte de la relativité restreinte et tant que nous nous limitons aux cadres de référence en mouvement inertiel, peu de choses importantes dépendent de la différence entre un cadre de référence inertiel et le système de coordonnées inertiel qu’il induit. Cette circonstance confortable cesse immédiatement dès que nous commençons à considérer les cadres de référence en mouvement non uniforme, même dans le cadre de la relativité restreinte….Plus récemment, pour négocier les ambiguïtés évidentes du traitement d’Einstein, la notion de cadre de référence est réapparue comme une structure distincte d’un système de coordonnées.
La discussion est portée au-delà des simples systèmes de coordonnées espace-temps par Brading et Castellani. L’extension aux systèmes de coordonnées utilisant des coordonnées généralisées sous-tend les formulations hamiltoniennes et lagrangiennes de la théorie quantique des champs, de la mécanique relativiste classique et de la gravité quantique.
Systèmes de coordonnéesModifier
Bien que le terme « système de coordonnées » soit souvent utilisé (notamment par les physiciens) dans un sens non technique, il a une signification précise en mathématiques, et c’est parfois ce que le physicien veut dire aussi.
Un système de coordonnées en mathématiques est une facette de la géométrie ou de l’algèbre, en particulier, une propriété des collecteurs (par exemple, en physique, les espaces de configuration ou les espaces de phase). Les coordonnées d’un point r dans un espace à n dimensions sont simplement un ensemble ordonné de n nombres :
r = . {\displaystyle \mathbf {r} =.}

Dans un espace de Banach général, ces nombres pourraient être (par exemple) des coefficients dans une expansion fonctionnelle comme une série de Fourier. Dans un problème physique, il peut s’agir de coordonnées spatio-temporelles ou d’amplitudes de mode normal. Dans la conception d’un robot, il peut s’agir d’angles de rotations relatives, de déplacements linéaires ou de déformations d’articulations. Ici, nous supposerons que ces coordonnées peuvent être reliées à un système de coordonnées cartésiennes par un ensemble de fonctions :
x j = x j ( x , y , z , … ) , j = 1 , … , n , {\displaystyle x^{j}=x^{j}(x,\ y,\ z,\ \dots ),\quad j=1,\ \dots ,\ n,

où x, y, z, etc. sont les n coordonnées cartésiennes du point. Étant donné ces fonctions, les surfaces de coordonnées sont définies par les relations:
x j ( x , y , z , … ) = c o n s t a n t , j = 1 , … , n . {\displaystyle x^{j}(x,y,z,\dots )=\mathrm {constant} ,\quad j=1,\\\N- points ,\N- n.}

L’intersection de ces surfaces définit des lignes de coordonnées. En tout point choisi, les tangentes aux lignes de coordonnées qui se croisent en ce point définissent un ensemble de vecteurs de base {e1, e2, …, en} en ce point. C’est-à-dire :
e i ( r ) = lim ϵ → 0 r ( x 1 , … , x i + ϵ , … , x n ) – r ( x 1 , … , x i , … , x n ) ϵ , i = 1 , … , n , {\displaystyle \mathbf {e} _{i}(\mathbf {r} )=\lim _{\epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},\\dots ,\ x^{i}+\epsilon ,\dots ,\ x^{n}\right)-\mathbf {r} \left(x^{1},\ \ \dots ,\ x^{i},\ \dots ,\ x^{n}\right)}{\epsilon }},\quad i=1,\ \dots ,\ n,}

qui peut être normalisé pour être de longueur unitaire. Pour plus de détails, voir coordonnées curvilignes.
Les surfaces de coordonnées, les lignes de coordonnées et les vecteurs de base sont des composantes d’un système de coordonnées. Si les vecteurs de base sont orthogonaux en chaque point, le système de coordonnées est un système de coordonnées orthogonales.
Un aspect important d’un système de coordonnées est son tenseur métrique gik, qui détermine la longueur d’arc ds dans le système de coordonnées en fonction de ses coordonnées :
( d s ) 2 = g i k d x i d x k , {\displaystyle (ds)^{2}=g_{ik}\ dx^{i}\ dx^{k},}

où les indices répétés sont additionnés.
Comme il ressort de ces remarques, un système de coordonnées est une construction mathématique, faisant partie d’un système axiomatique. Il n’y a pas de lien nécessaire entre les systèmes de coordonnées et le mouvement physique (ou tout autre aspect de la réalité). Cependant, les systèmes de coordonnées peuvent inclure le temps comme coordonnée et peuvent être utilisés pour décrire le mouvement. Ainsi, les transformations de Lorentz et les transformations galiléennes peuvent être vues comme des transformations de coordonnées.
Les sujets généraux et spécifiques des systèmes de coordonnées peuvent être poursuivis en suivant les liens Voir aussi ci-dessous.
Cadres de référence observationnelsModifier

Un cadre de référence d’observation, souvent appelé cadre de référence physique, un cadre de référence ou simplement un cadre, est un concept physique lié à un observateur et à l’état de mouvement de l’observateur. Nous adoptons ici le point de vue exprimé par Kumar et Barve : un cadre de référence observationnel est caractérisé uniquement par son état de mouvement. Cependant, il n’y a pas d’unanimité sur ce point. En relativité restreinte, on fait parfois la distinction entre un observateur et un cadre. Selon ce point de vue, un cadre est un observateur plus un réseau de coordonnées construit pour être un ensemble orthonormé de vecteurs spatiaux perpendiculaires à un vecteur temporel. Voir Doran. Cette vision restreinte n’est pas utilisée ici, et n’est pas universellement adoptée même dans les discussions sur la relativité. En relativité générale, l’utilisation de systèmes de coordonnées générales est courante (voir, par exemple, la solution de Schwarzschild pour le champ gravitationnel à l’extérieur d’une sphère isolée).
Il existe deux types de référentiel d’observation : inertiel et non inertiel. Un cadre de référence inertiel est défini comme celui dans lequel toutes les lois de la physique prennent leur forme la plus simple. En relativité restreinte, ces référentiels sont reliés par des transformations de Lorentz, qui sont paramétrées par la rapidité. En mécanique newtonienne, une définition plus restreinte exige seulement que la première loi de Newton soit vraie ; c’est-à-dire qu’un cadre inertiel newtonien est un cadre dans lequel une particule libre se déplace en ligne droite à vitesse constante, ou est au repos. Ces cadres sont reliés par des transformations galiléennes. Ces transformations relativistes et newtoniennes sont exprimées dans des espaces de dimension générale en termes de représentations du groupe de Poincaré et du groupe de Galilée.
Par opposition au cadre inertiel, un cadre de référence non inertiel est un cadre dans lequel des forces fictives doivent être invoquées pour expliquer les observations. Un exemple est un cadre de référence observationnel centré sur un point de la surface de la Terre. Ce cadre de référence tourne autour du centre de la Terre, ce qui introduit les forces fictives connues sous le nom de force de Coriolis, force centrifuge et force gravitationnelle. (Toutes ces forces, y compris la gravité, disparaissent dans un cadre de référence réellement inertiel, qui est celui de la chute libre.)
Appareil de mesureModification
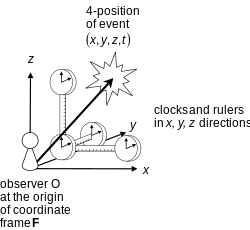
Un autre aspect d’un cadre de référence est le rôle de l’appareil de mesure (par exemple, les horloges et les tiges) attaché au cadre (voir la citation de Norton ci-dessus). Cette question n’est pas abordée dans cet article, et présente un intérêt particulier en mécanique quantique, où la relation entre l’observateur et la mesure est encore en discussion (voir problème de la mesure).
Dans les expériences de physique, le cadre de référence dans lequel les appareils de mesure du laboratoire sont au repos est généralement appelé cadre de laboratoire ou simplement « cadre de laboratoire ». Un exemple serait le cadre dans lequel les détecteurs d’un accélérateur de particules sont au repos. Dans certaines expériences, le cadre de laboratoire est un cadre inertiel, mais il n’est pas nécessaire qu’il le soit (par exemple, le laboratoire à la surface de la Terre dans de nombreuses expériences de physique n’est pas inertiel). Dans les expériences de physique des particules, il est souvent utile de transformer les énergies et les moments des particules du cadre de laboratoire où elles sont mesurées, au cadre du centre de momentum « cadre COM » dans lequel les calculs sont parfois simplifiés, puisque potentiellement toute l’énergie cinétique encore présente dans le cadre COM peut être utilisée pour fabriquer de nouvelles particules.
À ce propos, on peut noter que les horloges et les tiges souvent utilisées pour décrire l’équipement de mesure des observateurs en pensée, en pratique sont remplacées par une métrologie beaucoup plus compliquée et indirecte qui est liée à la nature du vide, et utilise des horloges atomiques qui fonctionnent selon le modèle standard et qui doivent être corrigées pour la dilatation du temps gravitationnel. (Voir seconde, mètre et kilogramme).
En fait, Einstein estimait que les horloges et les tiges n’étaient que des dispositifs de mesure expéditifs et qu’ils devaient être remplacés par des entités plus fondamentales basées, par exemple, sur les atomes et les molécules.
Les horloges et les tiges ne sont pas des instruments de mesure.