DéfinitionEdit
Le modèle tente d’expliquer un ensemble de p observations chez chacun des n individus avec un ensemble de k facteurs communs (F) où il y a moins de facteurs par unité que d’observations par unité (k<p). Chaque individu possède k de ses propres facteurs communs, et ceux-ci sont reliés aux observations via la matrice de charge factorielle ( L ∈ R p × k {\displaystyle L\in \mathbb {R} ^{p\times k}}.

), pour une seule observation, selon x i , m – μ i = l i , 1 f 1 , m + ⋯ + l i , k f k , m + ϵ i , m {\displaystyle x_{i,m}-\mu _{i}=l_{i,1}f_{1,m}+\dots +l_{i,k}f_{k,m}+\epsilon _{i,m}}

où ϵ i , m {\displaystyle \epsilon _{i,m}}

est le terme d’erreur stochastique inobservé de moyenne zéro et de variance finie, et μ i {\displaystyle \mu _{i}}.

est la moyenne de la ième observation.
En notation matricielle
X – M = L F + ϵ {\displaystyle X-\mathrm {M} =LF+\epsilon }

où la matrice d’observation X ∈ R p × n {\displaystyle X\in \mathbb {R} ^{p\times n}}.

, matrice de facteurs F ∈ R k × n {\displaystyle F\in \mathbb {R} ^{k\times n}}.

, matrice des termes d’erreur ϵ ∈ R p × n {\displaystyle \epsilon \in \mathbb {R} ^{p\times n}}

et matrice moyenne M ∈ R p × n {\displaystyle \mathrm {M} \in \mathbb {R} ^{p\times n}}

où l’élément i, m est simplement μ i {\displaystyle \mu _{i}}.

.
De plus, nous allons imposer les hypothèses suivantes sur F {\displaystyle F}.

:
- F et ϵ {\displaystyle \epsilon }.
sont indépendants.
- E ( F ) = 0 {\displaystyle \mathrm {E} (F)=0}
; où E est l’espérance
- C o v ( F ) = I {\displaystyle \mathrm {Cov} (F)=I}
où Cov est la matrice de covariance, pour s’assurer que les facteurs ne sont pas corrélés, et I est la matrice d’identité.
Supposons que C o v ( X – M ) = Σ {\displaystyle \mathrm {Cov} (X-\mathrm {M} )=\Sigma }.

. Alors Σ = C o v ( X – M ) = C o v ( L F + ϵ ) , {\displaystyle \Sigma =\mathrm {Cov} (X-\mathrm {M} )=\mathrm {Cov} (LF+\epsilon ),\,}

et donc, d’après les conditions imposées à F ci-dessus,
Σ = L C o v ( F ) L T + C o v ( ϵ ) , {\displaystyle \Sigma =L\mathrm {Cov} (F)L^{T}+\mathrm {Cov} (\epsilon ),\,

ou, en fixant Ψ = C o v ( ϵ ) {\displaystyle \Psi =\mathrm {Cov} (\epsilon )}

, Σ = L L L T + Ψ .

Notez que pour toute matrice orthogonale Q, si nous fixons L ′ = L Q isplaystyle L^{\prime }=LQ}.

et F ′ = Q T F {\displaystyle F^{\prime }=Q^{T}F}.

, les critères pour être des facteurs et des charges factorielles tiennent toujours. Par conséquent, un ensemble de facteurs et de charges factorielles n’est unique que jusqu’à une transformation orthogonale.
ExempleEdit
Supposons qu’un psychologue ait l’hypothèse qu’il existe deux types d’intelligence, « l’intelligence verbale » et « l’intelligence mathématique », dont aucune n’est directement observée. La preuve de l’hypothèse est recherchée dans les notes d’examen de chacun des 10 domaines universitaires différents de 1000 étudiants. Si chaque étudiant est choisi au hasard dans une grande population, alors les 10 notes de chaque étudiant sont des variables aléatoires. L’hypothèse du psychologue peut dire que pour chacun des 10 domaines universitaires, le score moyen sur le groupe de tous les étudiants qui partagent une paire de valeurs communes pour les « intelligences » verbale et mathématique est une constante multipliée par leur niveau d’intelligence verbale plus une autre constante multipliée par leur niveau d’intelligence mathématique, c’est-à-dire qu’il s’agit d’une combinaison linéaire de ces deux « facteurs ». Les nombres pour un sujet particulier, par lesquels les deux types d’intelligence sont multipliés pour obtenir le score attendu, sont supposés par l’hypothèse être les mêmes pour toutes les paires de niveaux d’intelligence, et sont appelés « charge factorielle » pour ce sujet. Par exemple, l’hypothèse peut indiquer que l’aptitude moyenne prédite d’un élève dans le domaine de l’astronomie est
{10 × l’intelligence verbale de l’élève} + {6 × l’intelligence intellectuelle de l’élève}. + {6 × l’intelligence mathématique de l’élève}.
Les nombres 10 et 6 sont les charges factorielles associées à l’astronomie. D’autres matières scolaires peuvent avoir des charges factorielles différentes.
Deux élèves supposés avoir des degrés identiques d’intelligence verbale et mathématique peuvent avoir des aptitudes mesurées différentes en astronomie parce que les aptitudes individuelles diffèrent des aptitudes moyennes (prédites ci-dessus) et à cause de l’erreur de mesure elle-même. De telles différences constituent ce que l’on appelle collectivement » l’erreur » – un terme statistique qui signifie la quantité par laquelle un individu, tel que mesuré, diffère de ce qui est moyen pour ou prédit par ses niveaux d’intelligence (voir erreurs et résidus en statistiques).
Les données observables qui entrent dans l’analyse factorielle seraient 10 scores de chacun des 1000 étudiants, soit un total de 10 000 nombres. Les charges factorielles et les niveaux des deux types d’intelligence de chaque élève doivent être déduits des données.
Modèle mathématique du même exempleModifier
Dans ce qui suit, les matrices seront indiquées par des variables indexées. Les indices « sujets » seront indiqués à l’aide de lettres a {\displaystyle a}

, b {\displaystyle b}

et c {\displaystyle c}

, avec des valeurs allant de 1 {\displaystyle 1}

à p {\displaystyle p}

qui est égal à 10 {\displaystyle 10}.

dans l’exemple ci-dessus. Les indices « facteurs » seront indiqués à l’aide des lettres p {\displaystyle p}.

, q {\displaystyle q}

et r {\displaystyle r}

, avec des valeurs allant de 1 isplaystyle 1}

à k {\displaystyle k}

qui est égal à 2 {\displaystyle 2}

dans l’exemple ci-dessus. Les indices « d’instance » ou « d’échantillon » seront indiqués par les lettres i {\displaystyle i}.

, j {\displaystyle j}

et k {\displaystyle k}

, avec des valeurs allant de 1 isplaystyle 1}

à N {\displaystyle N}

. Dans l’exemple ci-dessus, si un échantillon de N = 1000 {\displaystyle N=1000}

étudiants ont participé à la p = 10 {\displaystyle p=10}

examens, le i {\displaystyle i}

e étudiant pour le a {\displaystyle a}

e examen est donné par x a i {\displaystyle x_{ai}}.

. Le but de l’analyse factorielle est de caractériser les corrélations entre les variables x a {\displaystyle x_{a}}.

dont les x a i {\displaystyle x_{ai}}.

sont une instance particulière, ou un ensemble d’observations. Pour que les variables soient sur un pied d’égalité, elles sont normalisées en scores standards z {\displaystyle z}.

: z a i = x a i – μ a σ a {\displaystyle z_{ai}={\frac {x_{ai}-\mu _{a}}{sigma _{a}}}}

où la moyenne de l’échantillon est:
μ a = 1 N ∑ i x a i {\displaystyle \mu _{a}={\tfrac {1}{N}}\sum _{i}x_{ai}}

et la variance de l’échantillon est donnée par :
σ a 2 = 1 N – 1 ∑ i ( x a i – μ a ) 2 {\displaystyle \sigma _{a}^{2}={\tfrac {1}{N-1}}\sum _{i}(x_{ai}-\mu _{a})^{2}}

Le modèle d’analyse factorielle pour cet échantillon particulier est alors :
z 1 , i = ℓ 1 , 1 F 1 , i + ℓ 1 , 2 F 2 , i + ε 1 , i ⋮ ⋮ ⋮ ⋮ z 10 , i = ℓ 10 , 1 F 1 , i + ℓ 10 , 2 F 2 , i + ε 10 , i {\displaystyle {\begin{matrix}z_{1,i}&&\ell _{1,1}F_{1,i}&&\ell _{1,2}F_{2,i}&&\varepsilon _{1,i}\\\\N- &&\N- &&\vdots &&\vdots \z_{10,i}&&\ell _{10,1}F_{1,i}&&\ell _{10,2}F_{2,i}&&\varepsilon _{10,i}\end{matrix}}}

ou, plus succinctement :
z a i = ∑ p ℓ a p F p i + ε a i {\displaystyle z_{ai}=\sum _{p}\ell _{ap}F_{pi}+\varepsilon _{ai}}

où
- F 1 i {\displaystyle F_{1i}}
est l’i {\displaystyle i}
e « intelligence verbale » de l’élève,
- F 2 i {\displaystyle F_{2i}}.
est le i {\displaystyle i}.
l' »intelligence mathématique » de l’élève,
- ℓ a p {\displaystyle \ell _{ap}}.
sont les charges factorielles pour le a {\displaystyle a}
e sujet, pour p = 1 , 2 {\displaystyle p=1,2}
.
En notation matricielle, on a
Z = L F + ε {\displaystyle Z=LF+\varepsilon }.

Observez qu’en doublant l’échelle sur laquelle « l’intelligence verbale » – la première composante de chaque colonne de F {\displaystyle F}…

– est mesurée, et en divisant simultanément par deux les charges factorielles pour l’intelligence verbale ne fait aucune différence pour le modèle. Ainsi, on ne perd aucune généralité en supposant que l’écart-type des facteurs pour l’intelligence verbale est de 1 {\displaystyle 1}.

. De même pour l’intelligence mathématique. De plus, pour des raisons similaires, on ne perd aucune généralité en supposant que les deux facteurs ne sont pas corrélés entre eux. En d’autres termes : ∑ i F p i F q i = δ p q {\displaystyle \sum _{i}F_{pi}F_{qi}=\delta _{pq}}

where δ p q {\displaystyle \delta _{pq}}

est le delta de Kronecker ( 0 {\displaystyle 0}

lorsque p ≠ q {\displaystyle p\neq q}.

et 1 {\displaystyle 1}

when p = q {\displaystyle p=q}

).On suppose que les erreurs sont indépendantes des facteurs : ∑ i F p i ε a i = 0 {\displaystyle \sum _{i}F_{pi}\varepsilon _{ai}=0}

Notez que, puisque toute rotation d’une solution est également une solution, cela rend l’interprétation des facteurs difficile. Voir les inconvénients ci-dessous. Dans cet exemple particulier, si nous ne savons pas au préalable que les deux types d’intelligence ne sont pas corrélés, alors nous ne pouvons pas interpréter les deux facteurs comme les deux types d’intelligence différents. Même s’ils sont non corrélés, nous ne pouvons pas dire quel facteur correspond à l’intelligence verbale et quel facteur correspond à l’intelligence mathématique sans argument extérieur.
Les valeurs des loadings L {\displaystyle L}

, les moyennes μ {\displaystyle \mu }.

, et les variances des « erreurs » ε {\displaystyle \varepsilon }.

doivent être estimées étant donné les données observées X {\displaystyle X}

et F {\displaystyle F}.

(l’hypothèse sur les niveaux des facteurs est fixe pour un F {\displaystyle F} donné.

). Le « théorème fondamental » peut être dérivé des conditions ci-dessus : ∑ i z a i z b i = ∑ j ℓ a j ℓ b j + ∑ i ε a i ε b i {\displaystyle \sum _{i}z_{ai}z_{bi}=\sum _{j}\ell _{aj}\ell _{bj}+\sum _{i}\varepsilon _{ai}\varepsilon _{bi}}.

Le terme de gauche est le ( a , b ) {\displaystyle (a,b)}

-terme de la matrice de corrélation (a p × p {\displaystyle p\times p}).

matrice dérivée comme le produit des p × N {\displaystyle p\times N}

matrice des observations normalisées avec sa transposée) des données observées, et de son p {\displaystyle p}.

éléments diagonaux seront 1 {\displaystyle 1}.

s. Le deuxième terme à droite sera une matrice diagonale avec des termes inférieurs à l’unité. Le premier terme à droite est la « matrice de corrélation réduite » et sera égal à la matrice de corrélation, sauf pour ses valeurs diagonales qui seront inférieures à l’unité. Ces éléments diagonaux de la matrice de corrélation réduite sont appelés » communalités » (qui représentent la fraction de la variance de la variable observée qui est expliquée par les facteurs) : h a 2 = 1 – ψ a = ∑ j ℓ a j ℓ a j {\displaystyle h_{a}^{2}=1-\psi _{a}=\sum _{j}\ell _{aj}\ell _{aj}}.

Les données échantillons z a i {\displaystyle z_{ai}}

n’obéiront évidemment pas exactement à l’équation fondamentale donnée ci-dessus en raison des erreurs d’échantillonnage, de l’inadéquation du modèle, etc. Le but de toute analyse du modèle ci-dessus est de trouver les facteurs F p i {\displaystyle F_{pi}}.

et les chargements ℓ a p {\displaystyle \ell _{ap}}.

qui, dans un certain sens, donnent un « meilleur ajustement » aux données. Dans l’analyse factorielle, le meilleur ajustement est défini comme le minimum de l’erreur quadratique moyenne dans les résidus hors diagonale de la matrice de corrélation : ε 2 = ∑ a ≠ b 2 {\displaystyle \varepsilon ^{2}=\sum _{a\neq b}\left^{2}}.

Cela revient à minimiser les composantes hors diagonale de la covariance des erreurs qui, dans les équations du modèle, ont des valeurs attendues de zéro. Ceci est à opposer à l’analyse en composantes principales qui cherche à minimiser l’erreur quadratique moyenne de tous les résidus. Avant l’avènement des ordinateurs à grande vitesse, des efforts considérables ont été déployés pour trouver des solutions approximatives au problème, notamment en estimant les communalités par d’autres moyens, ce qui simplifie ensuite considérablement le problème en donnant une matrice de corrélation réduite connue. Celle-ci a ensuite été utilisée pour estimer les facteurs et les charges. Avec l’avènement des ordinateurs à haute vitesse, le problème de minimisation peut être résolu itérativement avec une vitesse adéquate, et les communalités sont calculées dans le processus, plutôt que d’être nécessaires au préalable. L’algorithme MinRes est particulièrement adapté à ce problème, mais il n’est guère le seul moyen itératif de trouver une solution.
Si l’on permet aux facteurs de solution d’être corrélés (comme dans la rotation » oblimin « , par exemple), alors le modèle mathématique correspondant utilise des coordonnées obliques plutôt que des coordonnées orthogonales.
Interprétation géométriqueEdit
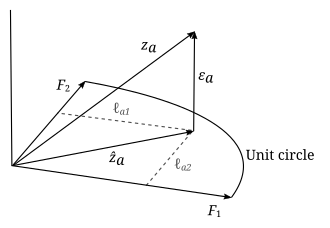

, qui est projeté sur un plan défini par deux vecteurs orthonormés F 1 {\displaystyle \mathbf {F} _{1}}

et F 2 {\displaystyle \mathbf {F} _{2}}

. Le vecteur de projection est z ^ a {\displaystyle {\hat {\mathbf {z}}. }}_{a}}

et l’erreur ε a {\displaystyle {\boldsymbol {\varepsilon }}_{a}}.

est perpendiculaire au plan, ce qui fait que z a = z ^ a + ε a {\displaystyle \mathbf {z} _{a}={\hat {\mathbf {z} }}_{a}+{\boldsymbol {\varepsilon }}_{a}}

. Le vecteur de projection z ^ a {\displaystyle {\hat {\mathbf {z}}}+{\boldsymbol {\varepsilon }}
. }}_{a}}

peut être représenté en termes de vecteurs facteurs comme z ^ a = ℓ a 1 F 1 + ℓ a 2 F 2 {\displaystyle {\hat {\mathbf {z}}. }}_{a}=\ell _{a1}\mathbf {F} _{1}+\Nell _{a2}\mathbf {F} _{2}}

. Le carré de la longueur du vecteur de projection est la communalité : | | z ^ a | | 2 = h a 2 {\displaystyle ||{\hat {\mathbf {z}} }}_{a}||^{2}=h_{a}^{2}}

. Si un autre vecteur de données z b {\displaystyle \mathbf {z} _{b}}

ont été tracés, le cosinus de l’angle entre z a {\displaystyle \mathbf {z}} _{a}}

et z b {\displaystyle \mathbf {z}} _{b}}

serait r a b {\displaystyle r_{ab}}.

: le ( a , b ) {\displaystyle (a,b)}

-entrée dans la matrice de corrélation. (Adapté de Harman Fig. 4.3)
Les paramètres et les variables de l’analyse factorielle peuvent recevoir une interprétation géométrique. Les données ( z a i {\displaystyle z_{ai}}

), les facteurs ( F p i {\displaystyle F_{pi}}

) et les erreurs ( ε a i {\displaystyle \varepsilon _{ai}}.

) peuvent être considérées comme des vecteurs dans un N {\displaystyle N}.

-dimensionnel (espace échantillon), représenté par z a {\displaystyle \mathbf {z} _{a}}

, F j {\displaystyle \mathbf {F} _{j}}

et ε a {\displaystyle {\boldsymbol {\varepsilon }}_{a}}

respectivement. Comme les données sont normalisées, les vecteurs de données sont de longueur unitaire ( | | z a | | = 1 {\displaystyle ||\mathbf {z} _{a}||=1}

). Les vecteurs facteurs définissent un k {\displaystyle k}

-dimensionnel (c’est-à-dire un hyperplan) dans cet espace, sur lequel les vecteurs de données sont projetés orthogonalement. Ceci découle de l’équation modèle z a = ∑ j ℓ a j F j + ε a {\displaystyle \mathbf {z} _{a}=\sum _{j}\ell _{aj}\mathbf {F} _{j}+{\boldsymbol {\varepsilon }}_{a}}

et l’indépendance des facteurs et des erreurs : F j ⋅ ε a = 0 {\displaystyle \mathbf {F} _{j}\cdot {\boldsymbol {\varepsilon }}_{a}=0}

. Dans l’exemple ci-dessus, l’hyperplan est simplement un plan à deux dimensions défini par les deux vecteurs de facteurs. La projection des vecteurs de données sur l’hyperplan est donnée par z ^ a = ∑ j ℓ a j F j {\displaystyle {\hat {\mathbf {z} }}_{a}=\sum _{j}\ell _{aj}\mathbf {F} _{j}}

et les erreurs sont des vecteurs de ce point projeté vers le point de données et sont perpendiculaires à l’hyperplan. Le but de l’analyse factorielle est de trouver un hyperplan qui est un « meilleur ajustement » aux données dans un certain sens, donc la façon dont les vecteurs facteurs qui définissent cet hyperplan sont choisis n’a pas d’importance, tant qu’ils sont indépendants et se trouvent dans l’hyperplan. Nous sommes libres de les spécifier comme étant à la fois orthogonaux et normaux ( F j ⋅ F q = δ p q {\displaystyle \mathbf {F} _{j}\cdot \mathbf {F} _{q}=\delta _{pq}}

) sans perte de généralité. Après avoir trouvé un ensemble approprié de facteurs, on peut aussi les faire pivoter arbitrairement dans l’hyperplan, de sorte que toute rotation des vecteurs facteurs définira le même hyperplan, et sera aussi une solution. Par conséquent, dans l’exemple ci-dessus, dans lequel l’hyperplan d’ajustement est bidimensionnel, si nous ne savons pas à l’avance que les deux types d’intelligence ne sont pas corrélés, nous ne pouvons pas interpréter les deux facteurs comme les deux types d’intelligence différents. Même s’ils sont non corrélés, nous ne pouvons pas dire quel facteur correspond à l’intelligence verbale et quel facteur correspond à l’intelligence mathématique, ou si les facteurs sont des combinaisons linéaires des deux, sans un argument extérieur.
Les vecteurs de données z a {\displaystyle \mathbf {z} _{a}}

ont une longueur unitaire. Les entrées de la matrice de corrélation pour les données sont données par r a b = z a ⋅ z b {\displaystyle r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}}

. La matrice de corrélation peut être interprétée géométriquement comme le cosinus de l’angle entre les deux vecteurs de données z a {\displaystyle \mathbf {z}} _{a}}

et z b {\displaystyle \mathbf {z}}

. Les éléments diagonaux seront clairement 1 {\displaystyle 1}

s et les éléments hors diagonale auront des valeurs absolues inférieures ou égales à l’unité. La « matrice de corrélation réduite » est définie comme suit : r ^ a b = z ^ a ⋅ z ^ b {\displaystyle {\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}}

.
Le but de l’analyse factorielle est de choisir l’hyperplan d’ajustement de telle sorte que la matrice de corrélation réduite reproduise la matrice de corrélation aussi fidèlement que possible, sauf pour les éléments diagonaux de la matrice de corrélation dont on sait qu’ils ont une valeur unitaire. En d’autres termes, l’objectif est de reproduire le plus fidèlement possible les corrélations croisées dans les données. Plus précisément, pour l’hyperplan d’ajustement, l’erreur quadratique moyenne dans les composantes hors diagonale
ε 2 = ∑ a ≠ b ( r a b – r ^ a b ) 2 {\displaystyle \varepsilon ^{2}=\sum _{a\neq b}\left(r_{ab}-{\hat {r}}_{ab}\right)^{2}}.

Il faut le minimiser, et cela se fait en le minimisant par rapport à un ensemble de vecteurs facteurs orthonormaux. On voit que
r a b – r ^ a b = ε a ⋅ ε b {\displaystyle r_{ab}-{\hat {r}}_{ab}={\boldsymbol {\varepsilon }}_{a}\cdot {\boldsymbol {\varepsilon }}_{b}}.

Le terme de droite est juste la covariance des erreurs. Dans le modèle, la covariance des erreurs est déclarée être une matrice diagonale et donc le problème de minimisation ci-dessus donnera en fait un « meilleur ajustement » au modèle : Il donnera une estimation de l’échantillon de la covariance des erreurs dont les composantes hors diagonale sont minimisées au sens du carré moyen. On constate que puisque le z ^ a {\displaystyle {\hat {z}}_{a}}

sont des projections orthogonales des vecteurs de données, leur longueur sera inférieure ou égale à la longueur du vecteur de données projeté, qui est l’unité. Les carrés de ces longueurs sont simplement les éléments diagonaux de la matrice de corrélation réduite. Ces éléments diagonaux de la matrice de corrélation réduite sont connus sous le nom de » communalités » : h a 2 = | z ^ a | | 2 = ∑ j ℓ a j 2 {\displaystyle {h_{a}}^{2}=|{\hat {\mathbf {z} {\a}||^{2}=\sum _{j}{\i1}-ell _{aj}}^{2}}






