L’efficacité d’un algorithme dépend de la quantité de temps, de stockage et d’autres ressources nécessaires pour exécuter l’algorithme. L’efficacité est mesurée à l’aide de notations asymptotiques.
Un algorithme peut ne pas avoir les mêmes performances pour différents types d’entrées. Avec l’augmentation de la taille de l’entrée, les performances vont changer.
L’étude du changement des performances de l’algorithme avec le changement de l’ordre de la taille de l’entrée est définie comme une analyse asymptotique.
Notations asymptotiques
Les notations asymptotiques sont les notations mathématiques utilisées pour décrire le temps d’exécution d’un algorithme lorsque l’entrée tend vers une valeur particulière ou une valeur limite.
Par exemple : Dans le tri à bulles, lorsque le tableau d’entrée est déjà trié, le temps pris par l’algorithme est linéaire c’est-à-dire le meilleur cas.
Mais, lorsque le tableau d’entrée est en état inverse, l’algorithme prend le temps maximum (quadratique) pour trier les éléments c’est-à-dire le pire cas.
Lorsque le tableau d’entrée n’est ni trié ni en état inverse, alors il prend un temps moyen. Ces durées sont dénotées à l’aide de notations asymptotiques.
Il existe principalement trois notations asymptotiques :
- Notation Big-O
- Notation Oméga
- Notation Thêta
Notation Big-O (O-notation)
La notation Big-O représente la borne supérieure du temps d’exécution d’un algorithme. Ainsi, elle donne la complexité du pire cas d’un algorithme.
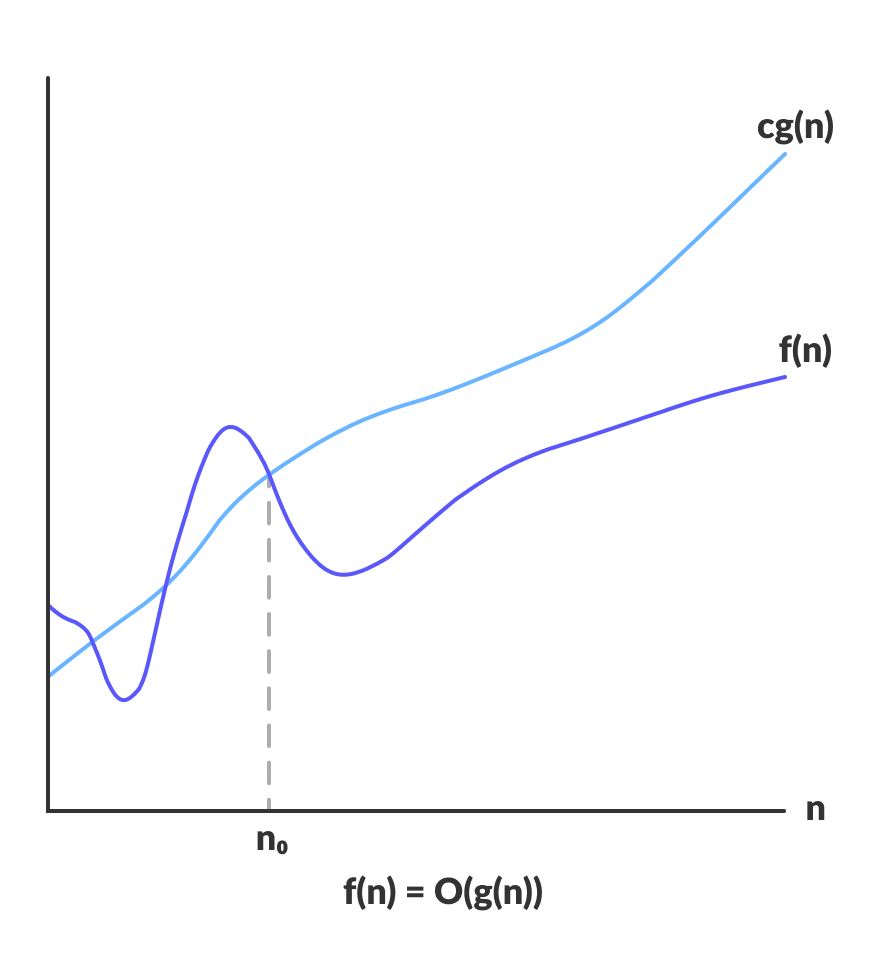
O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }
L’expression ci-dessus peut être décrite comme une fonction f(n). appartient à l’ensemble O(g(n)) s’il existe une constante positive c telle qu’elle soit comprise entre 0 et cg(n), pour des n suffisamment grandes.
Pour toute valeur de n, le temps d’exécution d’un algorithme ne croise pas le temps fourni par O(g(n)).
Puisqu’elle donne le temps d’exécution le plus défavorable d’un algorithme, elle est largement utilisée pour analyser un algorithme car nous sommes toujours intéressés par le scénario le plus défavorable.
Notation Oméga (Ω-notation)
La notation Oméga représente la borne inférieure du temps d’exécution d’un algorithme. Ainsi, elle fournit la complexité du meilleur cas d’un algorithme.

Ω(g(n)) = { f(n): there exist positive constants c and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }
L’expression ci-dessus peut être décrite comme une fonction. f(n) appartient à l’ensemble Ω(g(n)) s’il existe une constante positive c telle qu’elle soit supérieure à cg(n), pour une n suffisamment grande.
Pour toute valeur de n, le temps minimum requis par l’algorithme est donné par Oméga Ω(g(n)).
Notation thêta (Θ-notation)
La notation thêta englobe la fonction par le haut et par le bas. Comme elle représente la borne supérieure et la borne inférieure du temps d’exécution d’un algorithme, elle est utilisée pour analyser la complexité moyenne d’un algorithme.
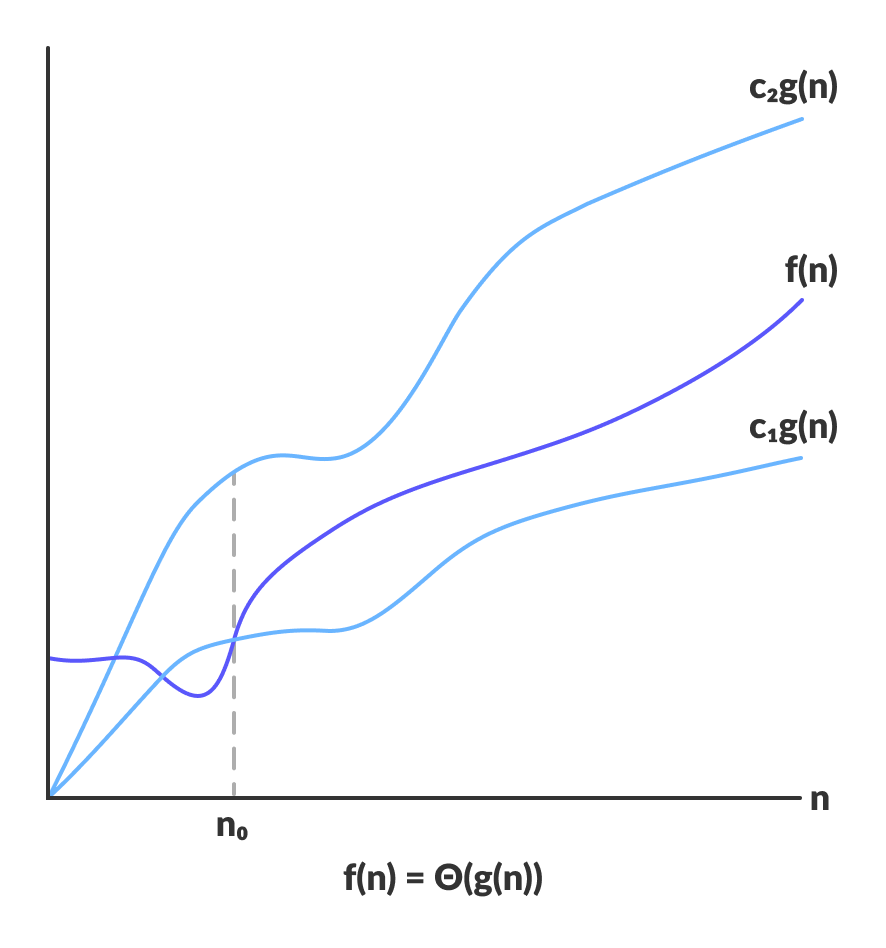
Pour une fonction g(n)Θ(g(n)) est donnée par la relation :
Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }
L’expression ci-dessus peut être décrite comme une fonction f(n) appartient à l’ensemble Θ(g(n)) s’il existe des constantes positives c1 et c2 telles qu’elle puisse être prise en sandwich entre c1g(n) et c2g(n), pour un nombre n suffisamment grand.
Si une fonction f(n) se trouve n’importe où entre c1g(n) et c2g(n) pour toutes les n ≥ n0, alors f(n) on dit que la borne est asymptotiquement serrée.