La force de Coriolis est un élément central de la dynamique des écoulements océaniques et atmosphériques. Une dérivation rigoureuse utilisant le calcul vectoriel est donnée dans de nombreux manuels de mécanique classique, mais ces dérivations ne sont souvent pas le moyen le plus efficace d’obtenir une compréhension conceptuelle. Par conséquent, nous fournirons ici une explication qualitative plus intuitive. Tout au long de ce chapitre sur les écoulements géophysiques, nous avons beaucoup parlé de la deuxième loi de Newton, mais la clé pour comprendre la force de Coriolis est plutôt la première loi de Newton : un objet en mouvement reste en mouvement à la même vitesse et dans la même direction, sauf s’il est soumis à une force déséquilibrée. La Terre et tout ce qui s’y trouve est en mouvement constant, puisque la Terre tourne autour de son axe. De plus, la direction de ce mouvement change constamment : lorsque vous tapez sur votre bureau à 14 heures, vous vous déplacez dans la direction exactement opposée à celle que vous aviez lorsque vous étiez allongé dans votre lit à 2 heures du matin. Ces changements forcés dans la direction du mouvement d’objets qui ont tendance à continuer à se déplacer dans la même direction est ce qui donne lieu à ce qu’on appelle les pseudo-forces (qui sont en fait très réelles, s’il se trouve que vous vivez sur une planète en rotation comme la Terre).
La pseudo-force la plus facile à comprendre conceptuellement est la force centrifuge, représentée ci-dessous.
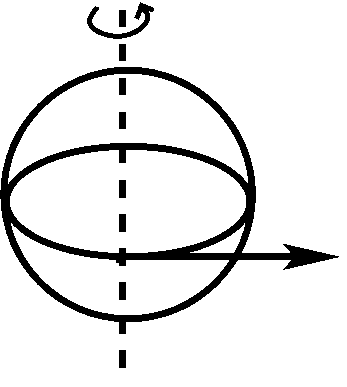
Essentiellement, les objets ont tendance à être éjectés d’un corps en rotation, car les objets continuent à se déplacer en ligne droite (comme indiqué par la flèche), tandis que la surface du corps en rotation ne se déplace pas en ligne droite (comme indiqué par le cercle). Heureusement, nous n’avons pas à craindre d’être éjectés de la Terre, car la force gravitationnelle qui maintient nos pieds sur le sol est environ 300 fois plus forte que la force centrifuge. La force centrifuge ne joue aucun rôle significatif dans la dynamique de l’océan et de l’atmosphère, mais elle rend la Terre légèrement elliptique.
La force de Coriolis est une pseudo-force qui émerge lorsqu’un objet se déplace à la surface d’un corps en rotation. La force de Coriolis est conceptuellement beaucoup plus subtile que la force centrifuge et, en fait, consiste en deux effets différents, chacun illustré ci-dessous :
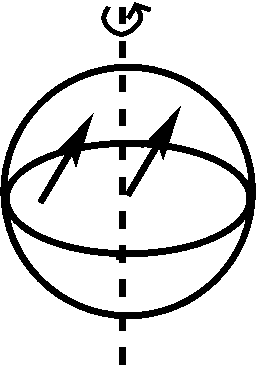
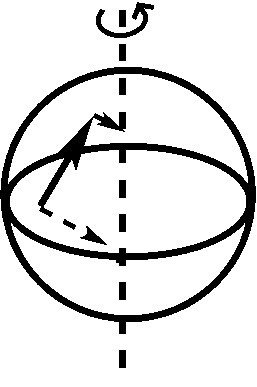
Le panneau de gauche illustre le premier effet : un objet qui continue à se déplacer dans la même direction dans l’espace absolu semble changer de direction, lorsque la Terre tourne vers la droite. Au début, l’objet se déplace droit vers le nord en direction du pôle (flèche gauche), mais ensuite, la direction du mouvement devient nord-est dans le référentiel terrestre (flèche droite), même si la direction et la vitesse de l’objet n’ont pas changé dans l’espace absolu. Le panneau de droite illustre le second effet : lorsqu’un objet se déplace à la surface de la Terre (comme indiqué par la flèche pleine), il emporte avec lui la vitesse de rotation de la Terre (flèches en pointillés). Lorsque l’objet se déplace vers le nord, il entre dans des régions où la vitesse de rotation de la Terre est plus faible qu’à son emplacement d’origine. Ainsi, il aura une vitesse excédentaire vers l’est qui déviera le mouvement du nord vers le nord-est, lorsqu’il est vu dans le cadre de référence de la Terre. Dans le référentiel terrestre, chacun de ces deux effets entraîne une accélération dont la magnitude est égale à \(\Omega \times v \sin\theta \) (avec \(\Omega \) la vitesse angulaire de la Terre, \(v\) la vitesse de l’objet dans le référentiel terrestre, et \(\theta\) la latitude), l’accélération totale s’élève donc à \(2 \times \Omega \times v \sin\theta\) ou \(f \times v\), avec le paramètre de Coriolis \(f = 2 \times \Omega \times \sin\theta\). La force de Coriolis forme un angle de \(90^{\circ}\) par rapport au mouvement de l’objet, vers la droite dans l’hémisphère nord, vers la gauche dans l’hémisphère sud ; elle s’annule à l’équateur (\(\theta=0\)). Dans les directions zonale et méridionale, les accélérations s’élèvent à :
\
L’impact de la force de Coriolis sur des parcelles d’air (ou d’eau) en mouvement est démontré ici.
Contributeurs
-
Dr Anne Willem Omta (MIT)
.