
Je vais être honnête. Je fais des calculs sérieux depuis plus d’années que je ne voudrais l’admettre. Parfois, en physique, il faut juste intégrer des trucs. C’est ce qui arrive.
Cependant, lorsque j’aidais mon fils avec son cours de calcul, j’ai commencé à réaliser – que diable se passe-t-il avec l’intégration ? J’ai l’impression d’avoir une compréhension vraiment solide des dérivés – mais l’intégration a des choses bizarres.
Eh bien, vous n’allez jamais comprendre les choses jusqu’à ce que vous les décomposiez en pièces de base. Donc, c’est ce que je vais faire. Je vais trouver l’aire sous une courbe de trois façons différentes.
Aire en utilisant la notation de sommation
C’est la plus facile à comprendre, mais la plus difficile à calculer. Oh attendez ! Pourquoi trouvons-nous l’aire sous une courbe ? OK, attendez – mon exemple à la fin devrait vous aider.
Donc, l’idée de base est de diviser une aire en N rectangles (où N est juste un certain nombre). Je peux ensuite trouver l’aire de chaque rectangle et les additionner pour obtenir l’aire totale. Plus je la découpe en morceaux, meilleure est la réponse – je vais donc écrire une expression pour cette aire et prendre la limite lorsque le nombre de morceaux va vers l’infini.

L’aire serait alors calculée comme suit :
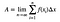
.
Il y a beaucoup de choses après cela – et cela devient un peu fastidieux. Cependant, vous DEVEZ passer par là pour bien comprendre l’ensemble. Voici une vidéo dans laquelle je vous guide à travers cette étape.
Si vous utilisez une fonction :
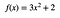
L’aire de x = 1 à x =2 est de 9 (quelles que soient les unités – je ne suis pas mathématicien, donc ça me dérange de ne pas indiquer les unités).
Aire utilisant des anti-dérivées
Il existe une astuce. C’est une astuce géniale. Vous pouvez écrire l’aire sous une courbe comme une intégrale définie (où l’intégrale est une somme infinie de morceaux infiniment petits – tout comme la notation de sommation).
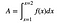
Maintenant pour les trucs fous. FOLLE. Il s’avère que l’aire est l’anti-dérivée de f(x). Si vous vous arrêtez un instant, vous verrez que c’est sauvage. Follement fou. Si la dérivée vous dit quelque chose sur la pente d’une courbe, l’opposé de la dérivée vous dit quelque chose sur l’aire sous la courbe ?
Oui. C’est le théorème fondamental du calcul. Voici mon explication (oui, il va y avoir un tas de vidéos dans ce post et vous êtes OBLIGÉS de les regarder toutes.
En fait, il y a une autre chose importante ici. L’intégrale définie de x = 1 à x =2 est la différence de la fonction d’aire A(2) et A(1). Je ne vais pas entrer dans les détails pour cela parce que mon esprit est encore soufflé par cette histoire d’anti-dérivée.
Mais voici l’aire sous la MÊME fonction mais avec intégration.
Oui. Vous obtenez le même résultat final. Aire = 9 poulets² (j’ai ajouté les unités d’aire).
Aire à l’aide de calculs numériques
Maintenant, nous passons aux choses amusantes. Et si je trouvais l’aire sous une courbe en additionnant l’aire d’un tas de rectangles ? Oh attends… j’ai déjà fait ça dans la première méthode. Mais que diriez-vous de ceci : je ne fais pas un nombre infini de rectangles, je fais juste un grand nombre de rectangles ? C’est exactement ce qu’est un calcul numérique.
Bien sûr, si je casse une zone en 100 morceaux, je vais devoir faire 100 séries de calculs de zone. Est-ce que quelqu’un veut vraiment faire cela ? Non – personne ne pense que ce serait amusant. Mais vous savez qui s’en moque ? Les ordinateurs (ordinateurs électroniques).
Oui, nous pouvons demander à un ordinateur de faire cette série de calculs. Nous avons juste besoin de lui donner quelques instructions et ensuite il ira faire son travail. Il sera génial. Voici la recette de base qu’il utilisera.
- Décidez en combien de morceaux vous voulez casser la courbe. Que diriez-vous de 100 ? Avec cela et la valeur x de début et de fin, vous pouvez calculer la largeur de chaque rectangle (Δx).
- Définissez la zone à zéro (poules²). Nous allons continuer à ajouter à cette valeur, mais il faut bien commencer quelque part.
- Démarrez avec la valeur initiale de x (dans l’exemple que j’ai utilisé – c’est x = 1).
- Calculez la hauteur du rectangle. Ce serait f(x) à la valeur x actuelle.
- Trouver la surface de ce rectangle et l’ajouter à la surface totale.
- Déplacer sur la valeur x suivante et répéter jusqu’à ce que vous arriviez à la valeur x finale.
C’est tellement simple que même un ordinateur pourrait le faire. OK, je m’amuse juste. Certains de mes meilleurs amis sont des ordinateurs.
Voici le code de ce calcul en python (voici un lien vers le code réel).
def f(t):
return(3*t**2+2)N=100x1=1
x2=2dx=(x2-x1)/N
A=0
x=x1
while x<=x2:
dA=f(x)*dx
A=A+dA
x=x+dx
print("A = ",A)
Avec N = 100, j’obtiens une surface de 8,95505 – ce qui n’est PAS exactement 9 poulets², mais c’est assez proche. Assez proche pour la plupart des calculs de poulets carrés.
Juste quelques commentaires rapides sur ce code.
- J’ai pensé qu’il serait amusant de faire de la fonction une véritable fonction python (c’est la partie
def f(t):. - Je calcule d’abord l’aire du minuscule rectangle (dA) et je l’ajoute ensuite à l’aire totale.
- Cette méthode a en fait des rectangles alignés avec la fonction sur le côté gauche du haut du rectangle. Vous pourriez le faire avec le côté droit aussi.
- J’ai également fait une vidéo pour cela. Mais vous n’êtes pas obligé de la regarder – je l’ai surtout déjà expliqué ici.
Et si vous n’avez pas de fonction mathématique ?
Laissez-moi vous mettre dans la situation suivante. Vous êtes dans une voiture qui roule et vous ne voyez QUE le compteur de vitesse. Vous notez la valeur de la vitesse toutes les secondes (parce que vous êtes un preneur de notes super rapide). La voiture finit par s’arrêter et vous devez trouver la distance que vous avez parcourue.
Voici quelque chose comme ça (en utilisant un chariot Vernier avec un capteur de mouvement – mais vous avez l’idée que c’est la même chose qu’une voiture réelle).

OK – avertissement, Je vais tricher ici. La piste Vernier collecte les données de position en fonction de ces lignes sur la piste. À partir de ces données de position, elle calcule la vélocité. J’ai donc déjà la position du chariot, mais supposons qu’il ne donne que la vitesse en fonction du temps. Cela ressemblerait peut-être à quelque chose comme ceci .

Vous voyez. Ce n’est pas une fonction – c’est une station spatiale. Non, attends, ça vient de Star Wars. Mais quand même, ce n’est pas une fonction mathématique. C’est juste des données. Vous ne pouvez pas trouver l’anti-dérivée des données (enfin, pas en utilisant les règles normales et autres). Mais attendez ! L’intégration numérique fonctionne très bien.
Bien sûr, il y a autre chose d’important ici. C’est l’idée que l’are sous cette courbe représente quelque chose de réel. Imaginez que vous ayez une voiture qui se déplace à une vitesse constante pendant un certain temps. Vous pourriez calculer le déplacement assez facilement :
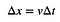
Si vous avez un tracé de la vitesse en fonction du temps. temps, cette vélocité constante ressemblerait à un rectangle. Oui, l’aire de ce rectangle serait v*Δt. Si ce n’est PAS une vitesse constante, l’aire sous le graphique vitesse-temps serait toujours le déplacement.
OK, une dernière vidéo. Voici mon explication du codage pour résoudre ce problème de déplacement.
Veillez à regarder toutes les vidéos.
.