Introducción
Esta página trata de las tensiones y deformaciones principales. Por ejemplo, si se calculan los valores principales de un tensor de tensiones de Cauchy, lo que se obtiene son las tensiones principales de Cauchy. Los valores principales de un tensor de deformación de Green serán las deformaciones principales de Green.
Todo lo que sigue se deduce de dos hechos: En primer lugar, los tensores de tensión y deformación de entrada son simétricos.En segundo lugar, las transformaciones de coordenadas discutidas aquí son aplicables a los tensores de tensión y deformación (de hecho lo son).
Hablaremos primero de la tensión y luego de la deformación.
Tensiones principales en 2D

En 2D, las ecuaciones de transformación son
Estas son las formas expandidas de \(\boldsymbol {\sigma}’ = {\bf Q} \cdot \boldsymbol {\sigma} \cdot {\bf Q}^T\) en 2-D.También se pueden derivar de un balance de fuerzas de la figura mostrada aquí. Es interesante que la tensión se caracterice como un tensor porque sigue la ecuación de transformación. Pero esto es principalmente un argumento matemático, y tendría poco peso si no estuviera conectado a la física del balance de fuerzas. El hecho de que la ecuación de transformación de coordenadas refleje adecuadamente el equilibrio de fuerzas en diferentes orientaciones es lo que lo hace relevante.
Las tensiones principales son las tensiones normales correspondientes a un ángulo, \(\theta_P\), en el que la tensión de cizallamiento, \(\tau’_{xy}\), es cero.
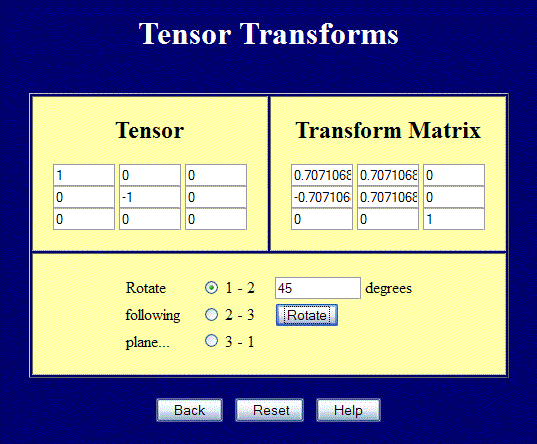
Esta página realiza transformaciones tensoriales completas en 3-D, pero todavía se puede utilizar para problemas en 2-D.. Introduzca los valores en las posiciones 2×2 de la parte superior izquierda y gire en el plano 1-2 para realizar transformaciones en 2-D. La captura de pantalla de abajo muestra un caso de cizallamiento puro rotado 45° para obtener las tensiones principales. Obsérvese también cómo se transforma la matriz \({\bf Q}\).
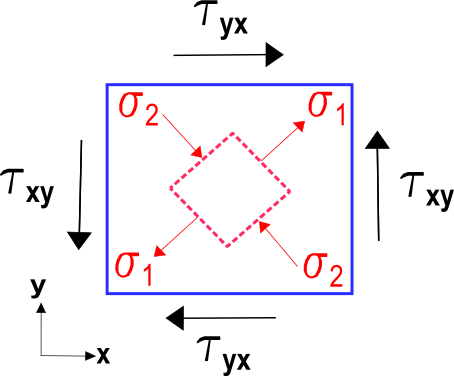
La figura de abajo muestra las tensiones correspondientes al caso de cizalla pura en el ejemplo de la página web de transformadas tensoriales. El cuadrado azul alineado con los ejes sufre claramente cizalladura.Pero el cuadrado rojo inscrito en el cuadrado azul más grande sólo ve tensión y compresión simples.Estos son los valores principales del caso de cizalladura pura en el sistema de coordenadas global.
En 2-D, la orientación de la tensión principal, \(\theta_P\), se puede calcular mediante el establecimiento de\(\tau’\!_{xy} = 0\) en la ecuación de cizallamiento anterior y resolver para \(\theta\)para obtener \(\theta_P\), el ángulo de la tensión principal. a matriz de transformación, ({\bf Q}), es
]
Insertando este valor de \(\theta_P\) en las ecuaciones de las tensiones normales se obtienen los valores principales. Se escriben como \_{máximo}{sigma} y \_{mínimo}{sigma}{mínimo}, o alternativamente como \_{sigma_1}{sigma_2}{sigma_2}{sigma_2}.
También podrían obtenerse utilizando \(\boldsymbol{\bigma}’ = {\bf Q} \cdot \boldsymbol{\bigma} \cdot {\bf Q}^T)con \cdot ({\bf Q}\) basado en \theta_P\).
Tensiones principales en 3-D
Las transformaciones de coordenadas en 3-D son
= \left\left\left]
La segunda matriz \({\bf Q}} es de nuevo la transposición de la primera.
Esta página realiza transformaciones tensoriales.
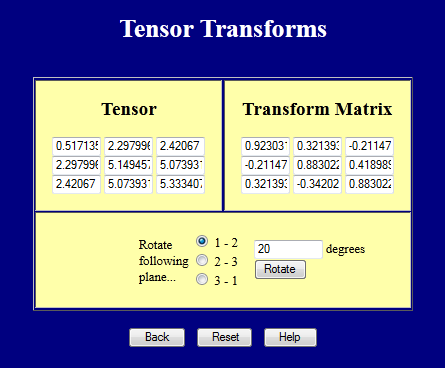
Y esta página calcula los valores principales (valores propios)y las direcciones principales (vectores propios).
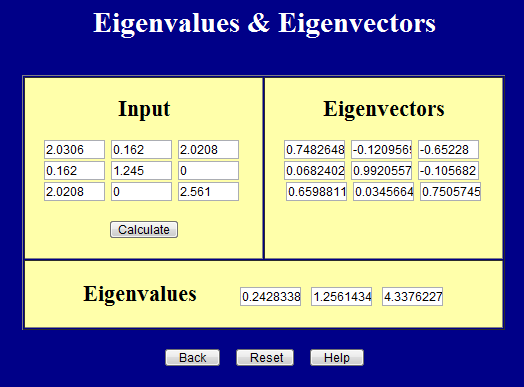
Es importante recordar que las entradas de ambas páginas deben ser simétricas. De hecho, ambas páginas lo exigen.
Los valores propios anteriores pueden escribirse en forma de matriz como
\N]
Deformaciones principales en 2-D
La mecánica de cálculo de las deformaciones principales es idéntica a la del cálculo de las tensiones principales. El único escollo potencial que hay que tener en cuenta es que las ecuaciones siempre operan sobre la mitad de los valores de cizalladura, \(\gamma / 2\).
En 2D, las ecuaciones de transformación son
\
Las ecuaciones se escriben en términos de \(\gamma / 2\) para enfatizar que la mitad de todos los valores de cizalladura se utilizan en las ecuaciones de transformación.
Esta página realiza transformaciones tensoriales completas en 3D, pero también puede utilizarse para problemas en 2D.. Introduzca los valores en las posiciones 2×2 de la parte superior izquierda y gire en el plano 1-2 para realizar las transformaciones en 2-D. La captura de pantalla de abajo muestra un caso de cizallamiento puro rotado 45° para obtener las tensiones principales. Obsérvese también cómo se transforma la matriz \({\bf Q}\).

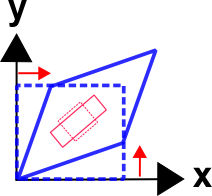
La figura de abajo muestra las formas deformadas correspondientes al caso de cizalla pura en el ejemplo de la página web de transformadas tensoriales. El cuadrado azul alineado con los ejes sufre claramente el cizallamiento.Pero el cuadrado rojo inscrito en el cuadrado azul más grande sólo ve la tensión y la compresión simples.Estos son los valores principales de la deformación de cizallamiento puro en el sistema de coordenadas global.
En 2D, la orientación de la deformación principal, \(\theta_P\), puede calcularse estableciendo(\gamma’\!_{xy} = 0\) en la ecuación de cizallamiento anterior y resolviendo para \(\theta\)para obtener \(\theta_P\), el ángulo de deformación principal. a matriz de transformación, ({\bf Q}), es
]
Insertando este valor de \(\theta_P\) en las ecuaciones de las tensiones normales se obtienen los valores principales. Se escriben como \\Nmáximo y \Nmínimo, o alternativamente como \N1 y \N2.
También podrían obtenerse utilizando \({\bf E}’ = {\bf Q} \cdot {\bf E} \cdot {\bf Q}^T)con \cdot ({\bf Q}) en función de \theta_P\).
Tensiones principales en 3-D
Las transformaciones de coordenadas en 3-D son
= \left\left\left]
La segunda matriz \({\bf Q}} es de nuevo la transposición de la primera.
Esta página realiza transformaciones tensoriales.

Y esta página calcula los valores principales (valores propios)y las direcciones principales (vectores propios).

Es importante recordar que las entradas de ambas páginas deben ser simétricas. De hecho, ambas páginas lo exigen.
Los valores propios anteriores pueden escribirse en forma matricial como
\N]
Resumen
\Ndonde \N({\bf A}\N) es «cualquier matriz simétrica».
Y recordemos que el producto de cualquier matriz con su transpuesta es siempre un resultado simétrico, por lo que este resultado cumpliría los requisitos. Esto es especialmente relevante para \N({\bf F}^T \cdot {\bf F}}), cuyas invariantes se utilizan en la Ley de Mooney-Rivlin sobre el comportamiento del caucho.La Ley de Mooney-Rivlin y los coeficientes se discutirán en esta página.Como un teaser añadido, veremos que la 3ª invariante de \({\bf F}^T \cdot {\bf F}} para el caucho siempre es igual a 1 porque el caucho es incompresible. Así que no sólo es una constante, independiente de las transformaciones de coordenadas, sino que incluso es un valor constante, siempre igual a 1, independiente de las transformaciones de coordenadas y del estado de deformación.