Marco de referencia

La necesidad de distinguir entre los diversos significados de «marco de referencia» ha dado lugar a una variedad de términos. Por ejemplo, a veces se adjunta el tipo de sistema de coordenadas como modificador, como en el marco de referencia cartesiano. A veces se hace hincapié en el estado de movimiento, como en el marco de referencia rotatorio. A veces se subraya la forma en que se transforma a los marcos considerados como relacionados, como en el marco de referencia galileano. A veces los marcos se distinguen por la escala de sus observaciones, como en los marcos de referencia macroscópicos y microscópicos.

En este artículo, el término marco de referencia observacional se utiliza cuando el énfasis se pone en el estado de movimiento más que en la elección de coordenadas o en el carácter de las observaciones o del aparato de observación. En este sentido, un marco de referencia observacional permite el estudio del efecto del movimiento sobre toda una familia de sistemas de coordenadas que podrían estar unidos a este marco. Por otra parte, un sistema de coordenadas puede emplearse para muchos fines en los que el estado de movimiento no es la principal preocupación. Por ejemplo, se puede adoptar un sistema de coordenadas para aprovechar la simetría de un sistema. En una perspectiva aún más amplia, la formulación de muchos problemas en física emplea coordenadas generalizadas, modos normales o vectores propios, que sólo están relacionados indirectamente con el espacio y el tiempo. Parece útil divorciar los distintos aspectos de un marco de referencia para la discusión que sigue. Por lo tanto, tomamos los marcos de referencia observacionales, los sistemas de coordenadas y los equipos de observación como conceptos independientes, separados como se indica a continuación:

• Un marco de observación (como un marco de referencia inercial o un marco de referencia no inercial) es un concepto físico relacionado con el estado de movimiento.
• Un sistema de coordenadas es un concepto matemático, que equivale a una elección del lenguaje utilizado para describir las observaciones. En consecuencia, un observador en un marco de referencia observacional puede elegir emplear cualquier sistema de coordenadas (cartesiano, polar, curvilíneo, generalizado, …) para describir las observaciones realizadas desde ese marco de referencia. Un cambio en la elección de este sistema de coordenadas no cambia el estado de movimiento de un observador, y por lo tanto no implica un cambio en el marco de referencia observacional del observador. Este punto de vista se puede encontrar también en otros lugares. Lo que no quiere decir que algunos sistemas de coordenadas puedan ser una mejor opción para algunas observaciones que otros.
• La elección de qué medir y con qué aparato de observación es una cuestión independiente del estado de movimiento del observador y de la elección del sistema de coordenadas.

Aquí hay una cita aplicable a los marcos de observación en movimiento R {\displaystyle {\mathfrak {R}}



y varios sistemas de coordenadas trispaciales euclidianos asociados :

Introducimos primero la noción de marco de referencia, relacionada a su vez con la idea de observador: el marco de referencia es, en cierto sentido, el «espacio euclidiano que lleva el observador». Demos una definición más matemática:… el marco de referencia es… el conjunto de todos los puntos del espacio euclidiano con el movimiento del cuerpo rígido del observador. El marco, denotado R {\displaystyle {\mathfrak {R}}



, se dice que se mueve con el observador…. Las posiciones espaciales de las partículas se etiquetan en relación con un marco R {\displaystyle {\mathfrak {R}}



estableciendo un sistema de coordenadas R con origen O. El correspondiente conjunto de ejes, que comparten el movimiento del cuerpo rígido del marco R {\displaystyle {\mathfrak {R}}



, puede considerarse que da una realización física de R {\displaystyle {\mathfrak {R}}



. En un marco R {\displaystyle {\mathfrak {R}}



, las coordenadas se cambian de R a R′ realizando, en cada instante de tiempo, la misma transformación de coordenadas sobre las componentes de los objetos intrínsecos (vectores y tensores) introducidos para representar las magnitudes físicas en este marco.

y esto sobre la utilidad de separar las nociones de R {\displaystyle {\mathfrak {R}}.



y :

Como señaló Brillouin, hay que distinguir entre conjuntos matemáticos de coordenadas y marcos físicos de referencia. El desconocimiento de tal distinción es fuente de mucha confusión… las funciones dependientes como la velocidad, por ejemplo, se miden con respecto a un marco de referencia físico, pero uno es libre de elegir cualquier sistema de coordenadas matemáticas en el que se especifiquen las ecuaciones.

y esto, también sobre la distinción entre R {\displaystyle {\mathfrak {R}}



y :

La idea de un marco de referencia es realmente muy diferente de la de un sistema de coordenadas. Los marcos se diferencian sólo cuando definen espacios (conjuntos de puntos de reposo) o tiempos (conjuntos de eventos simultáneos) diferentes. Así pues, las ideas de espacio y tiempo, de reposo y simultaneidad, van inextricablemente unidas a la de marco. Sin embargo, un simple desplazamiento del origen, o una rotación puramente espacial de las coordenadas espaciales, da lugar a un nuevo sistema de coordenadas. Así que los marcos corresponden, en el mejor de los casos, a clases de sistemas de coordenadas.

y de J. D. Norton:

En los desarrollos tradicionales de la relatividad especial y general se ha acostumbrado a no distinguir entre dos ideas bastante distintas. La primera es la noción de sistema de coordenadas, entendida simplemente como la asignación suave e invertible de cuatro números a los eventos en las vecindades del espaciotiempo. La segunda, el marco de referencia, se refiere a un sistema idealizado utilizado para asignar dichos números Para evitar restricciones innecesarias, podemos divorciar esta disposición de las nociones métricas. De especial importancia para nuestros propósitos es que cada marco de referencia tiene un estado de movimiento definido en cada evento del espaciotiempo. Dentro del contexto de la relatividad especial y siempre que nos limitemos a los marcos de referencia en movimiento inercial, entonces poco importante depende de la diferencia entre un marco de referencia inercial y el sistema de coordenadas inerciales que induce. Esta cómoda circunstancia cesa inmediatamente una vez que empezamos a considerar los marcos de referencia en movimiento no uniforme, incluso dentro de la relatividad especial….Más recientemente, para negociar las obvias ambigüedades del tratamiento de Einstein, la noción de marco de referencia ha reaparecido como una estructura distinta de un sistema de coordenadas.

La discusión se lleva más allá de los simples sistemas de coordenadas espacio-temporales por Brading y Castellani. La extensión a los sistemas de coordenadas que utilizan coordenadas generalizadas subyace en las formulaciones hamiltonianas y lagrangianas de la teoría cuántica de campos, la mecánica relativista clásica y la gravedad cuántica.

Sistemas de coordenadasEditar

Artículo principal: Sistemas de coordenadas

Ver también: Coordenadas generalizadas y Convenciones de los ejes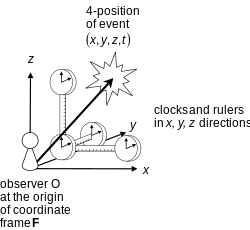



Un observador O, situado en el origen de un conjunto local de coordenadas – un marco de referencia F. El observador en este marco utiliza las coordenadas (x, y, z, t) para describir un evento del espaciotiempo, mostrado como una estrella.

Aunque el término «sistema de coordenadas» se utiliza a menudo (sobre todo por los físicos) en un sentido no técnico, el término «sistema de coordenadas» tiene un significado preciso en matemáticas, y a veces eso es lo que el físico quiere decir también.

Un sistema de coordenadas en matemáticas es una faceta de la geometría o del álgebra, en particular, una propiedad de los colectores (por ejemplo, en física, espacios de configuración o espacios de fase). Las coordenadas de un punto r en un espacio n-dimensional son simplemente un conjunto ordenado de n números:

r = .



En un espacio de Banach general, estos números podrían ser (por ejemplo) coeficientes en una expansión funcional como una serie de Fourier. En un problema físico, podrían ser coordenadas espaciotemporales o amplitudes de modos normales. En el diseño de un robot, podrían ser ángulos de rotaciones relativas, desplazamientos lineales o deformaciones de articulaciones. Aquí supondremos que estas coordenadas pueden relacionarse con un sistema de coordenadas cartesianas mediante un conjunto de funciones:

x j = x j ( x , y , z , … ) , j = 1 , … , n , {\displaystyle x^{j}=x^{j}(x,\ y,\ z,\dots ),\quad j=1,\dots ,\ n,



donde x, y, z, etc. son las n coordenadas cartesianas del punto. Dadas estas funciones, las superficies de coordenadas se definen mediante las relaciones:

x j ( x , y , z , … ) = c o n s t a n t , j = 1 , … , n . {\displaystyle x^{j}(x,y,z,\dots )=\mathrm {constante} ,\quad j=1,\dots ,\n.}



La intersección de estas superficies definen líneas de coordenadas. En cualquier punto seleccionado, las tangentes a las líneas de coordenadas que se cruzan en ese punto definen un conjunto de vectores base {e1, e2, …, en} en ese punto. Es decir:

e i ( r ) = lim ϵ → 0 r ( x 1 , … , x i + ϵ , … , x n ) – r ( x 1 , … , x i , … , x n ) ϵ , i = 1 , … , n , {\displaystyle \mathbf _{i}(\mathbf {r} )=lim _{epsilon \rightarrow 0}{frac {\mathbf {r} \izquierda (x^1}, puntos, x^i}+epsilon, puntos, x^n}derecha) -mathbf {r} \left(x^{1},\dots ,\ x^{i},\dots ,\ x^{n}\right)}{epsilon }},\quad i=1,\dots ,\ n,



que puede ser normalizado para ser de longitud unitaria. Para más detalles ver coordenadas curvilíneas.

Las superficies de coordenadas, las líneas de coordenadas y los vectores base son componentes de un sistema de coordenadas. Si los vectores base son ortogonales en cada punto, el sistema de coordenadas es un sistema de coordenadas ortogonal.

Un aspecto importante de un sistema de coordenadas es su tensor métrico gik, que determina la longitud de arco ds en el sistema de coordenadas en términos de sus coordenadas:

( d s ) 2 = g i k d x i d x k , {\displaystyle (ds)^{2}=g_{ik}\ dx^{i}\ dx^{k},}



donde se suman los índices repetidos.

Como se desprende de estas observaciones, un sistema de coordenadas es una construcción matemática, parte de un sistema axiomático. No hay ninguna conexión necesaria entre los sistemas de coordenadas y el movimiento físico (o cualquier otro aspecto de la realidad). Sin embargo, los sistemas de coordenadas pueden incluir el tiempo como una coordenada, y pueden utilizarse para describir el movimiento. Así, las transformaciones de Lorentz y las transformaciones galileanas pueden verse como transformaciones de coordenadas.

Los temas generales y específicos de los sistemas de coordenadas pueden seguirse siguiendo los enlaces Ver también que aparecen a continuación.

Marcos de referencia observacionalesEditar

Artículo principal: Marco de referencia inercial



Tres marcos de referencia en la relatividad especial. El marco negro está en reposo. El marco preparado se mueve al 40% de la velocidad de la luz, y el marco doblemente preparado al 80%. Obsérvese el cambio en forma de tijera a medida que aumenta la velocidad.

Un marco de referencia observacional, a menudo denominado marco de referencia físico, marco de referencia o simplemente marco, es un concepto físico relacionado con un observador y el estado de movimiento del observador. Aquí adoptamos la opinión expresada por Kumar y Barve: un marco de referencia observacional se caracteriza únicamente por su estado de movimiento. Sin embargo, no hay unanimidad sobre este punto. En la relatividad especial, a veces se distingue entre un observador y un marco de referencia. Según este punto de vista, un marco es un observador más una red de coordenadas construida para ser un conjunto ortonormal de vectores espaciales perpendiculares a un vector temporal. Véase Doran. Este punto de vista restringido no se utiliza aquí, y no se adopta universalmente incluso en las discusiones sobre la relatividad. En la relatividad general es común el uso de sistemas de coordenadas generales (véase, por ejemplo, la solución de Schwarzschild para el campo gravitatorio fuera de una esfera aislada).

Hay dos tipos de marco de referencia observacional: inercial y no inercial. Un marco de referencia inercial se define como aquel en el que todas las leyes de la física adoptan su forma más simple. En la relatividad especial, estos marcos se relacionan mediante transformaciones de Lorentz, parametrizadas por la rapidez. En la mecánica newtoniana, una definición más restringida sólo requiere que la primera ley de Newton se cumpla; es decir, un marco inercial newtoniano es aquel en el que una partícula libre se desplaza en línea recta a velocidad constante, o está en reposo. Estos marcos se relacionan mediante transformaciones galileanas. Estas transformaciones relativistas y newtonianas se expresan en espacios de dimensión general en términos de representaciones del grupo de Poincaré y del grupo de Galilea.

En contraste con el marco inercial, un marco de referencia no inercial es aquel en el que se deben invocar fuerzas ficticias para explicar las observaciones. Un ejemplo es un marco de referencia observacional centrado en un punto de la superficie de la Tierra. Este marco de referencia orbita alrededor del centro de la Tierra, lo que introduce las fuerzas ficticias conocidas como fuerza de Coriolis, fuerza centrífuga y fuerza gravitatoria. (Todas estas fuerzas, incluida la gravedad, desaparecen en un marco de referencia verdaderamente inercial, que es el de la caída libre.)

Aparato de mediciónEditar

Otro aspecto de un marco de referencia es el papel del aparato de medición (por ejemplo, relojes y varillas) unido al marco (véase la cita de Norton más arriba). Esta cuestión no se aborda en este artículo, y es de especial interés en la mecánica cuántica, donde la relación entre el observador y la medición sigue siendo objeto de debate (véase el problema de la medición).

En los experimentos de física, el marco de referencia en el que los aparatos de medición del laboratorio están en reposo suele denominarse marco de laboratorio o simplemente «marco de laboratorio». Un ejemplo sería el marco en el que están en reposo los detectores de un acelerador de partículas. El marco del laboratorio en algunos experimentos es un marco inercial, pero no es necesario que lo sea (por ejemplo, el laboratorio en la superficie de la Tierra en muchos experimentos de física no es inercial). En los experimentos de física de partículas, a menudo es útil transformar las energías y los momentos de las partículas desde el marco del laboratorio en el que se miden, al marco del centro de momento «marco COM» en el que a veces se simplifican los cálculos, ya que potencialmente toda la energía cinética aún presente en el marco COM puede utilizarse para fabricar nuevas partículas.

En este sentido, se puede señalar que los relojes y las varillas que a menudo se utilizan para describir el equipo de medición de los observadores en el pensamiento, en la práctica se sustituyen por una metrología mucho más complicada e indirecta que está conectada a la naturaleza del vacío, y utiliza los relojes atómicos que funcionan de acuerdo con el modelo estándar y que deben ser corregidos por la dilatación del tiempo gravitacional. (Véase segundo, metro y kilogramo).

De hecho, Einstein consideraba que los relojes y las varillas eran dispositivos de medición meramente expeditivos y que debían ser sustituidos por entidades más fundamentales basadas, por ejemplo, en átomos y moléculas.