Autómatas Finitos Deterministas
Un autómata finito determinista (AFD) se describe mediante una tupla de cinco elementos: (Q,Σ,δ,q0,F)(Q, \Sigma, \delta, q_0, F)(Q,Σ,δ,q0,F).
QQQ = un conjunto finito de estados
Σ\SigmaΣ = un alfabeto de entrada finito alfabeto de entrada no vacío
δ\deltaδ = una serie de funciones de transición
q0q_0q0 = el estado inicial
FFF = el conjunto de estados aceptantes
Debe haber exactamente una función de transición para cada símbolo de entrada en Σ\SigmaΣ de cada estado.
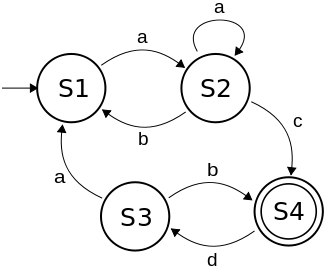
Los AFD pueden representarse mediante diagramas de esta forma: 

Utilizando el diagrama de estados del personaje del videojuego anterior, describe cómo un jugador puede controlar a su personaje para que pase de estar parado a correr y a saltar.
Mostrar respuestaEn el estado de parado, el jugador puede no pulsar nada y permanecer en el estado de parado, luego, para pasar al estado de corriendo, el usuario debe pulsar el botón «Arriba». En el estado de correr, el usuario puede seguir haciendo correr a su personaje pulsando el botón «Arriba», y luego, para hacer la transición al estado de saltar, el usuario debe pulsar «A».
Dibuja un diagrama para un AFD que reconozca el siguiente lenguaje: El lenguaje de todas las cadenas que terminan en 1.
Mostrar respuesta
Autómatas finitos no deterministas
QQQ = un conjunto finito de estados
Σ\SigmaΣ = un alfabeto finito, alfabeto de entrada no vacío
δ\deltaδ = una serie de funciones de transición
q0q_0q0 = el estado inicial
FFF = el conjunto de estados de aceptación
A diferencia de los DFAs, los NDFAs no están obligados a tener funciones de transición para cada símbolo en Σ\SigmaΣ, y puede haber múltiples funciones de transición en el mismo estado para el mismo símbolo. Además, los NDFAs pueden utilizar transiciones nulas, que se indican con ϵ\epsilonϵ. Las transiciones nulas permiten a la máquina saltar de un estado a otro sin tener que leer un símbolo.
Un NDFA acepta una cadena xxx si existe un camino compatible con esa cadena que termine en un estado de aceptación.
Los NDFAs pueden ser representados por diagramas de esta forma:
 source
source
Describe el lenguaje que reconoce el NDFA anterior.
Mostrar respuestaEl NDFA de arriba reconoce cadenas que terminan en «10» y cadenas que terminan en «01».
El estado aaa es el estado de inicio, y a partir de ahí, podemos crear una cadena con tantos 1’s y 0’s en cualquier orden, y luego transferir al estado bbb o al estado eee, o podemos transferir inmediatamente al estado bbb o al estado eee. En cualquier caso, el NDFA sólo aceptará una cadena que alcance el estado ddd o el estado ggg. Para alcanzar el estado ddd o el estado ggg, la cadena debe terminar con un «01» (para el estado ddd) o un «10» (para el estado ggg).
Por ejemplo, las siguientes cadenas son todas reconocidas por este NDFA.
- 00000000010
- 10
- 01
- 1111101

Dibuja un diagrama para el NDFA que describa el siguiente lenguaje: El lenguaje de todas las cadenas que terminan en 1.
Mostrar respuesta
.

