Introducción a la química – 1ª edición canadiense

Los gases estuvieron entre las primeras sustancias estudiadas utilizando el método científico moderno, que se desarrolló en el año 1600. No se tardó en reconocer que todos los gases compartían ciertos comportamientos físicos, lo que sugirió que los gases podían describirse mediante una teoría global. La teoría cinética molecular de los gases es un modelo que nos ayuda a comprender las propiedades físicas de los gases a nivel molecular. Se basa en los siguientes conceptos:

1. Los gases están formados por partículas (moléculas o átomos) que se encuentran en constante movimiento aleatorio.
2. Las partículas de los gases chocan constantemente entre sí y con las paredes de su contenedor. Estas colisiones son elásticas; es decir, no hay pérdida neta de energía por las colisiones.
3. Las partículas de gas son pequeñas y el volumen total ocupado por las moléculas de gas es insignificante en relación con el volumen total de su contenedor.
4. No hay fuerzas interactivas (es decir, atracción o repulsión) entre las partículas de un gas.
5. La energía cinética media de las partículas del gas es proporcional a la temperatura absoluta del gas, y todos los gases a la misma temperatura tienen la misma energía cinética media.

Figura 6.6 «La teoría molecular cinética de los gases» muestra una representación de cómo nos imaginamos mentalmente la fase gaseosa.



La teoría molecular cinética de los gases describe este estado de la materia como compuesto por partículas diminutas en constante movimiento con mucha distancia entre las partículas. Como la mayor parte del volumen ocupado por un gas es espacio vacío, un gas tiene una baja densidad y puede expandirse o contraerse bajo la influencia adecuada. El hecho de que las partículas del gas estén en constante movimiento significa que dos o más gases siempre se mezclarán, ya que las partículas de cada uno de los gases se mueven y chocan entre sí. El número de colisiones que las partículas de gas hacen con las paredes de su recipiente y la fuerza con la que colisionan determinan la magnitud de la presión del gas.

Energía cinética y velocidad molecular

Las partículas de gas están en constante movimiento, y cualquier objeto en movimiento tiene energía cinética (Ek). La energía cinética, para un átomo individual, puede calcularse mediante la siguiente ecuación donde m es la masa, y u es la velocidad.

Ek = 1/2 mu2

En general, las moléculas de una muestra de un gas comparten una energía cinética media; sin embargo, las moléculas individuales exhiben una distribución de energías cinéticas debido a que tienen una distribución de velocidades (Figura 6.7 «Distribución estilizada de la velocidad molecular»). Esta distribución de velocidades surge de las colisiones que se producen entre las moléculas en la fase gaseosa. Aunque estas colisiones son elásticas (no hay pérdida neta de energía), las velocidades individuales de cada molécula implicada en la colisión pueden cambiar. Por ejemplo, en la colisión de dos moléculas, una molécula puede desviarse a una velocidad ligeramente superior y la otra a una velocidad ligeramente inferior, pero la energía cinética media no cambia.



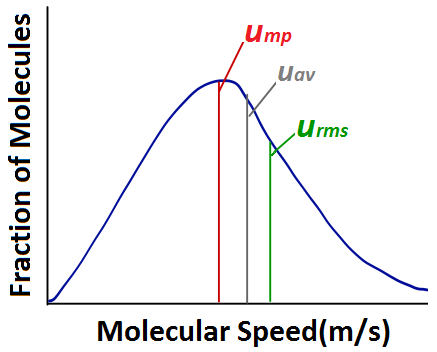
Al analizar un diagrama de la distribución de las velocidades moleculares, hay varios términos de uso común con los que hay que familiarizarse. La velocidad más probable (ump) es la velocidad del mayor número de moléculas, y corresponde al pico de la distribución. La velocidad media (uav) es la velocidad media de todas las moléculas de gas de la muestra. La velocidad media cuadrática (rms) corresponde a la velocidad de las moléculas que tienen exactamente la misma energía cinética que la energía cinética media de la muestra.



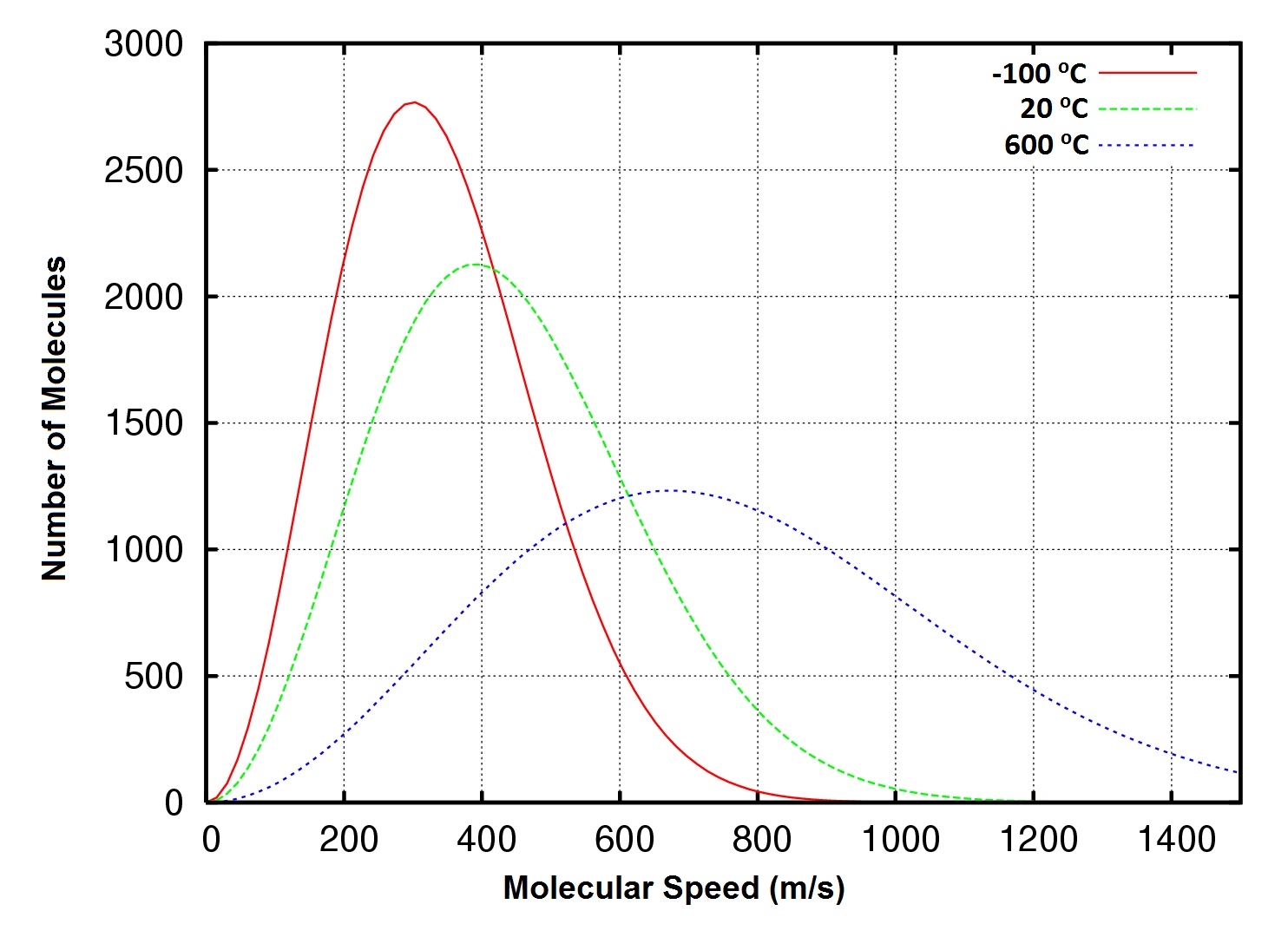
Figura 6.8 Distribución de las velocidades moleculares, gas oxígeno a -100, 20 y 600°C

Según la teoría cinética molecular, la energía cinética media de las partículas de gas es proporcional a la temperatura absoluta del gas. Esto se puede expresar con la siguiente ecuación donde k representa la constante de Boltzmann. La constante de Boltzmann es simplemente la constante del gas R dividida por la constante de Avogadro (NA). La barra encima de ciertos términos indica que son valores medios.

Superline{E_k} = \frac{3}{2} \textit{kT}

Dado que la energía cinética media está relacionada tanto con la temperatura absoluta como con la velocidad molecular, podemos combinar la ecuación anterior con la anterior para determinar la velocidad rms.

\textit{{ = }\frac{1}{2} \textit{m} \overline{u^2} \textit{ = } \frac{3}{2} \textit{kT}

$\sqrt{overline{u^2}} = \sqrt{\frac{3kT}{m}$

Esto demuestra que la velocidad rms está relacionada con la temperatura. Podemos manipular aún más esta ecuación multiplicando el numerador y el denominador por la constante de Avogadro (NA) para darnos una forma que utilice la constante de los gases (R) y la masa molar (M).

$\sqrt{overline{u^2}} = \sqrt{\frac{3RT}{M}}$

Esta forma de la ecuación demuestra que la velocidad rms de las moléculas del gas también está relacionada con la masa molar de la sustancia. Comparando dos gases de diferente masa molar a la misma temperatura, vemos que a pesar de tener la misma energía cinética media, el gas de menor masa molar tendrá una mayor velocidad rms.



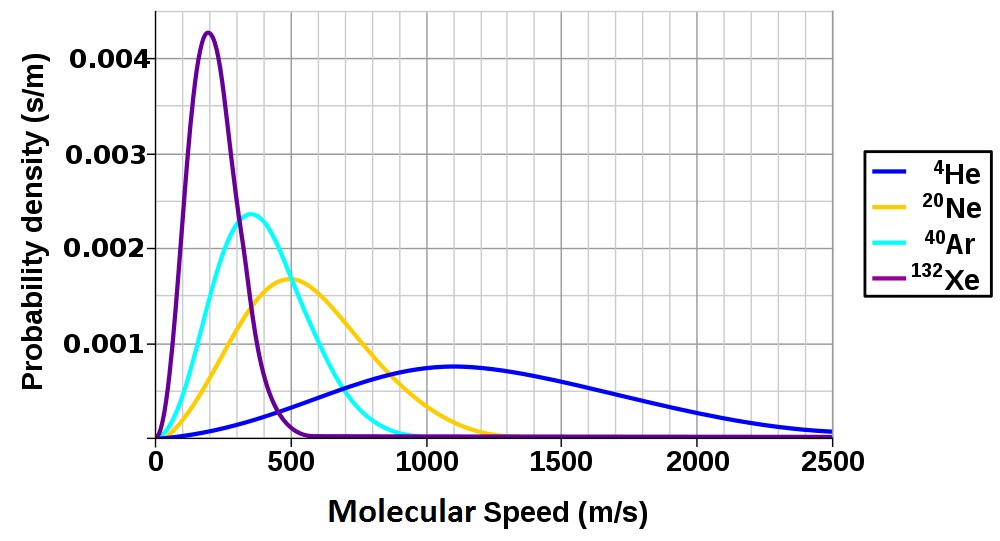
Figura 6.9 Distribución de la velocidad molecular de los gases nobles

Ejemplo 19
Calcular la velocidad eficaz de las moléculas de nitrógeno a 25ºC.Solución$\qrt{sobrelínea{u^2}=\qrt{frac{3RT}{M}=\qrt{frac{3(8,3145\ J{ K}^-1}{ mol}^-1})(298,15\ K)}{28,02\q\q\} {10}^-3}\ kg{ mol}^-1}}$$\qrt{sobrelínea{u^2}=\qrt{2.654\ x\ {10}^{5\}J\kg}^{-1}}$Sabiendo que 1 J = 1 kg m2 s-2 podemos convertir a metros por segundo: \sqrt{overline{u^2}}=\ \sqrt{2.654\ x\ {10}^5\ }J\kg}^{-1}\ \frac{1\ kg\ m^2{\ s}^{-2}}{1\ J}\ \sqrt{overline{u^2}}= \sqrt{2,654\ x10}^5\ }m^2{\ s}^{-2}}\textit{{515,2 m}{\} {\ s}^{-1} \textit{}

Aplicación de la teoría cinética molecular a las leyes de los gases

La teoría cinética molecular puede utilizarse para explicar o predecir las tendencias experimentales que se utilizaron para generar las leyes de los gases. Trabajemos con algunos escenarios para demostrar este punto.

¿Qué ocurrirá con la presión de un sistema en el que se disminuye el volumen a temperatura constante?

Este problema puede abordarse de dos maneras:

1. La ley de los gases ideales puede reordenarse para resolver la presión y estimar el cambio en la presión:

\textit{PV = nRT}

\textit{P = }\frac{nRT}{V}\textit{}

El volumen se encuentra en el denominador de la ecuación, y se está disminuyendo. Esto significa que el resto de la ecuación se está dividiendo por un número menor, por lo que debería hacer que la presión sea mayor.

2. Se puede utilizar la teoría cinética molecular. Como la temperatura se mantiene constante, la energía cinética media y la velocidad rms también permanecen iguales. El volumen del recipiente ha disminuido, lo que significa que las moléculas de gas tienen que moverse una distancia más corta para tener una colisión. Por lo tanto, habrá más colisiones por segundo, lo que provocará un aumento de la presión.

¿Qué ocurrirá con la presión de un sistema en el que se aumenta la temperatura y el volumen permanece constante?

De nuevo, este tipo de problema se puede enfocar de dos maneras:

1. La ley de los gases ideales puede reordenarse para resolver la presión y estimar el cambio de presión.

\textit{p = }\frac{nRT}{V}\textit{}

La temperatura se encuentra en el numerador; existe una relación directa entre la temperatura y la presión. Por tanto, un aumento de la temperatura debería provocar un aumento de la presión.

2. Se puede utilizar la teoría cinética molecular. La temperatura aumenta, por lo que la energía cinética media y la velocidad rms también deberían aumentar. Esto significa que las moléculas de gas golpearán las paredes del recipiente con más frecuencia y con mayor fuerza porque todas se mueven más rápido. Esto debería aumentar la presión.

Los puntos clave

• El comportamiento físico de los gases se explica mediante la teoría cinética molecular de los gases.
• El número de colisiones que las partículas de gas realizan con las paredes de su recipiente y la fuerza con la que chocan determinan la magnitud de la presión del gas.
• La temperatura es proporcional a la energía cinética media.

Ejercicios

1. Enunciar las ideas de la teoría cinética molecular de los gases.
2. Calcular la velocidad media del CO2 a 40°C.
3. Utilizando la teoría cinética molecular, explique cómo afecta a la presión un aumento del número de moles de gas a volumen y temperatura constantes.
4. Respuestas
   1. Los gases están formados por diminutas partículas de materia que están en constante movimiento. Las partículas del gas chocan constantemente entre sí y con las paredes de un recipiente. Estas colisiones son elásticas, es decir, no hay pérdida neta de energía por las colisiones. Las partículas de gas están separadas por grandes distancias. El tamaño de las partículas de gas es minúsculo en comparación con las distancias que las separan y el volumen del recipiente. No hay fuerzas interactivas (es decir, atracción o repulsión) entre las partículas de un gas. La energía cinética media de las partículas de un gas depende de la temperatura del mismo.
   2. 421 m/s
   3. La temperatura se mantiene igual, por lo que la energía cinética media y la velocidad rms deberían seguir siendo las mismas. El aumento del número de moles de gas significa que hay más moléculas de gas disponibles para chocar con las paredes del recipiente en cualquier momento. Por lo tanto, la presión debería aumentar.